おことわり。
このノートが、「2019年シミュレーション実習 Day5」の実習課題の内容です。こちらは、はやとちって先に終わらせてしまった去年(2018)のDay5の内容となっています。
色々なモデルのシミュレーションができた上、線形安定性解析について再び一から学ぶことのできる充実したスライドだったので、やる分には良かったと思います。
概要¶
| # | タイトル | キーワード |
|---|---|---|
| 0 | Introduction | ワディントン描像・分化・iPS細胞 |
| 1 | 大腸菌のコロニー増殖とその派生 | 平衡点・安定性 |
| 2 | Notch-Deltaの側方抑制モデル/a> | 多安定性・ピッチフォーク分岐 |
| 3 | LacYのポジティブ・フィードバックモデル | ヒステリシス・サドルノード分岐 |
| 4 | (発展課題)解糖系振動のモデル | リミットサイクル・ホップ分岐 |
今日のゴール
生物のモデルを使って力学系のキーワードを理解する
import numpy as np
import matplotlib.pyplot as plt
def simulation(ODE,vals,dt=0.1,min_t=0,max_t=100,**params):
"""
Simulate ODE numerically.
@param ODE: (function) Ordinary Differential Equation.
@param vals: (tuple/int,float) Initial value(s) for ODE simulation.
@param params: (kwargs) Parameter for ODE
"""
max_t+=dt
time = np.arange(min_t,max_t,dt)
Nval = len(vals) if type(vals) is tuple else 1
Vals = np.zeros((len(time),Nval))
if Nval==1:
for i,t in enumerate(time):
Vals[i] = vals
vals = ODE(vals,**params,dt=dt)
else:
for i,t in enumerate(time):
Vals[i] = vals
vals = ODE(*vals,**params,dt=dt)
return time,Vals
def plotVariousInitial(ax,ODE,
xmin,xmax,xspan,
otherval=None,
plotall=False,
colors=None,
dt=0.1,min_t=0,max_t=100,
**params):
"""
Simulate with various initial state(x).
NOTE: The type of `otherval` is (list)
"""
xmax+=xspan
xs = np.arange(xmin,xmax,xspan)
for x in xs:
x = tuple([x] + list(otherval)) if otherval else x
time, Xs = simulation(ODE=ODE,vals=x,**params,dt=dt,min_t=min_t,max_t=max_t)
if plotall:
for i in range(len(otherval)+1):
color = colors[i] if colors else None
ax.plot(time, Xs[:,i], color=color,label="initial x={}".format(x))
else:
ax.plot(time, Xs[:,0], color="red",label="initial x={}".format(x))
return ax
def plotStability(ax,x,y,stable,text=True):
"""Plot the stability"""
if stable:
ax.scatter(x,y,color="black",s=100)
if text: ax.annotate("stable",(x,y),textcoords="offset points",xytext=(10,0),size=20)
else:
ax.scatter(x,y, marker="o", color='white', edgecolors='black', s=100)
if text: ax.annotate("unstable",(x,y),textcoords="offset points",xytext=(10,0),size=20)
return ax
def P3_1D(ax,ODE,
xmin,xmax,xspan,
dt=1,
quiver_color="black",
**params):
"""
Plot Phase Portrait. (1D: variable x)
@param ODE: (function) Ordinary Differential Equation.
@param params: (kwargs) Parameter for ODE
"""
xmax+=xspan
xs = np.arange(xmin,xmax,xspan)
dX = ODE(xs,**params,dt=dt) - xs # NOTE: ODE returns "X+dX"
zs = np.zeros(dX.shape)
ax.quiver(zs,xs,zs,dX,color=quiver_color)
ax.tick_params(labelbottom=False,bottom=False)
title = "[params] " + ", ".join(["{}:{}".format(k,v) for k,v in params.items()])
ax.set_title(title)
ax.set_ylabel("Initial state(x)")
psign = np.sign(dX)[0]
for i,sign in enumerate(np.sign(dX)):
if sign==0 or (psign!=0 and sign!=psign):
x = xs[i] if sign==0 else (xs[i-1] + xs[i])/2
flag = dX[i+1]<0 if i==0 else psign>0
ax = plotStability(ax,x=0,y=x,stable=flag)
psign=sign
return ax
def plotBifurcationDiagram(ax,ODE,
pmin,pmax,pspan,pname,
xmin,xmax,xspan,xname,xindex=None,
dt=1,
quiver_color=None,
**params):
"""
Plot Bifurcation Diagram.
It shows the model's stability if "one parameter(p)" and "initial state(x)" changed.
@param ax: (AxesSubplot) Axes for plotting space.
@param ODE: (function) Ordinary Differential Equation.
@param *name: (str) Identify which parameter/initial state changed.
@param xindex: (int) Where is the changed state(x) in the ODE's returns.
@param params: (kwargs) Other fixed Parameter for ODE
"""
pRange = np.arange(pmin,pmax+pspan,pspan)
xRange = np.arange(xmin,xmax+xspan,xspan)
P,X = np.meshgrid(pRange,xRange)
params[pname] = P
params[xname] = X
XplusdX = ODE(**params,dt=dt) if xindex is None else ODE(**params,dt=dt)[xindex]
dX = XplusdX - X
dP = np.zeros(dX.shape)
ax.quiver(P,X,dP,dX,color=quiver_color)
return ax
def plotFinalState(ax,ODE,
pmin,pmax,pspan,pname,
xmin,xmax,xspan,xname,xindex=0,
otherstates=None,
min_t=0,max_t=100,dt=0.1,
color=None,
**params):
"""
Plot Final state(xname)
NOTE: The type of `otherstates` is (list)
"""
pRange = np.arange(pmin,pmax+pspan,pspan)
xRange = np.arange(xmin,xmax+xspan,xspan)
for p in pRange:
params[pname] = p
for x in xRange:
x = tuple(otherstates[:xindex] + [x] + otherstates[xindex:]) if otherstates else x
time, Xs = simulation(ODE=ODE,vals=x,**params,dt=dt,min_t=min_t,max_t=max_t)
ax.scatter(p,Xs[:,xindex][-1],marker="x",color=color)
return ax
def plotFunc2D(func,ax=None,xmin=-1,xmax=1,xspan=0.1,reverse=False,color=None,label=None,**kwargs):
"""
plot function curve on 2-dimensional space.
@param ax: (AxesSubplot) Axes for plotting space.
@param func: (function) any function.
@param params: (kwargs) Parameter for function.
"""
if ax==None:
fig, ax = plt.subplots()
xmax+=xspan
X = np.arange(xmin,xmax,xspan)
Y = np.vectorize(func)(X,**kwargs)
if reverse: X,Y = Y,X
ax.plot(X,Y,color=color,label=label)
return ax
0. Introduction
- iPS細胞(人工多能性幹細胞:induced pluripotent stem cell)は、「成熟細胞の分化状態をリセットし、多能性(pluripotency)を持つ」細胞のこと。
- 従来「細胞は坂を転がるボールである」(ワディントン描画)と言われており、「いったん分化(=本来同一だったものが多様化していくこと)すると、他の分化状態に移ることは難しい」とされていた。
- このワディントン描画を力学系の言葉に翻訳すると、超臨界ピッチフォーク分岐(supercritical pitchfork bifurcation)となり、この相互作用は背後にどんな複雑な遺伝子間相互作用があっても、$\frac{dx}{dt} = rx-x^3$ という標準形で近似される。(中心多様体縮約定理)
- このように、生物学における多くの重要概念が、力学系(Dynamical system, 時間変化するシステム)によって明確に定義ができる。
| 生物学 | 力学系 |
|---|---|
| 分化 | ピッチフォーク分岐 |
| 概日リズム | リミットサイクル |
| 細胞周期制御 | サドルノード分岐 |
| 神経発火 | 興奮系 |
※ 上は、かなり簡略した対応付けで、実際は一つの生命現象に複数の分岐が関わっていたりする。
1. 大腸菌のコロニー増殖とその派生
「細胞が一定時間ごとに分裂する(半分になる)」という「大腸菌のコロニー増殖」(「放射性元素の崩壊」)をモデル化する。
1.1 Malthusian mode¶
| 微分方程式 | $\frac{dx}{dt} = rx$ |
| $x$ | 個体数 |
| $r>0$ | 成長率(マルサス係数) |
| $r<0$ | 崩壊定数 |
| 初期値 | $x(0) = x_0$ |
| 解析解 | $x(t)=x_0e^{rt}=x_02^{\frac{r}{\log2}t}$ |
| 細胞周期の長さ | $\frac{\log2}{r}$ |
課題1-1:微分方程式を手で解く(紙と鉛筆)¶
$$ \begin{aligned} \frac{dx}{dt} &= rx\\ \int\frac{dx}{x} &= \int rdt\\ x &= Ae^{rt}\quad \left(A\text{: const.}\right)\\ \therefore\ x &= x_0e^{rt} = x_02^{\frac{r}{^log}t}\quad (\because\ t=0, x(t)=x_0) \end{aligned} $$課題1-2:微分方程式をシミュレーションする。¶
大腸菌増殖($r>0$,細胞が一定時間ごとに分裂する)の場合
def Malthusian_ODE(x,r,dt):
dx = r*x*dt
return x+dx
fig, ax = plt.subplots()
r=0.05
xmin=-2; xmax=2; xspan=1
ax = plotVariousInitial(ax,ODE=Malthusian_ODE,xmin=xmin,xmax=xmax,xspan=xspan,r=r)
ax.set_title("Malthusian model r={}".format(r))
ax.set_xlabel("Time(t)")
ax.set_ylabel("Population size (x)")
plt.show()
※ $x$ を個体数と考えた場合、負の値を取ることはありえないが、理解を深める上では有用なので、一応調べた。
課題1-3:微分方程式をシミュレーションする。¶
放射性元素の崩壊($r<0$, 元素の数が半減期を経るごとに半分)の場合
fig, ax = plt.subplots()
r=-0.05
xmin=-2; xmax=2; xspan=1
ax = plotVariousInitial(ax,ODE=Malthusian_ODE,xmin=xmin,xmax=xmax,xspan=xspan,r=r)
ax.set_title("Malthusian model r={}".format(r))
ax.set_xlabel("Time(t)")
ax.set_ylabel("Population size (x)")
plt.show()
※ $x$ を元素数と考えた場合、負の値を取ることはありえないが、理解を深める上では有用なので、一応調べた。
課題1-4:相図(Phase portrait)を描く¶
パラメータを変えた時の力学系の変化を見る。
fig = plt.figure(figsize=(8,6))
xmin=-2;xmax=2;xspan=0.5
rRange = [-0.05,0.05]
for i,r in enumerate(rRange):
ax1 = plt.subplot2grid((2, 4), (i, 0), colspan=3)
ax2 = plt.subplot2grid((2, 4), (i, 3))
ax1 = plotVariousInitial(ax1,ODE=Malthusian_ODE,xmin=xmin,xmax=xmax,xspan=xspan,r=r)
ax1.set_title("Malthusian model r={}".format(r))
ax1.set_xlabel("Time(t)")
ax1.set_ylabel("Population size (x)" if r>0 else "Radioactive element (x)")
ax2 = P3_1D(ax2,ODE=Malthusian_ODE,xmin=xmin,xmax=xmax,xspan=xspan,r=r)
plt.tight_layout()
plt.show()
参考:分岐図(bifurcation diagram)¶
パラメータを変えた時の力学系の変化を見る
def plotMalthusianBD(ax,ODE,dt=0.01,color="black",
rmin=-0.05,rmax=0.05,rspan=0.01,
xmin=-0.05,xmax=0.05,xspan=0.01,):
r = np.arange(rmin,rmax+rspan,rspan)
x = np.arange(xmin,xmax+xspan,xspan)
R,X = np.meshgrid(r,x)
dX = ODE(X,R,dt=dt) - X # NOTE: ODE returns "X+dX"
dR = np.zeros(dX.shape)
ax.quiver(R,X,dR,dX,color=color)
return ax
fig, ax = plt.subplots()
rmin=-0.05;rmax=0.06;rspan=0.01
xmin=-0.05;xmax=0.05;xspan=0.01
ax = plotBifurcationDiagram(ax, ODE=Malthusian_ODE,quiver_color="blue",
pmin=rmin,pmax=rmax,pspan=rspan,pname="r",
xmin=xmin,xmax=xmax,xspan=xspan,xname="x")
func1 = lambda x:0; ax = plotFunc2D(func=func1,ax=ax,color="red", label="$x=0$")
func2 = lambda y:0; ax = plotFunc2D(func=func2,reverse=True,ax=ax,color="red",label="$r=0$")
ax.set_title("bifurcation diagram")
ax.set_xlabel("Parameter (r)")
ax.set_ylabel("State variable (x)")
ax.set_xlim(rmin,rmax)
ax.set_ylim(xmin,xmax)
ax.legend()
plt.show()
1.2 Logistic model¶
個体の増殖に増減がある場合は、以下のようにロジスティックモデル(Logistic model)でモデル化できる。
| 微分方程式 | $\frac{dx}{dt} = r\left(1-\frac{x}{K}\right)$ |
| $x$ | 個体数 |
| $r>0$ | 成長率(マルサス係数) |
| $K$ | 環境収容力 |
| 初期値 | $x(0) = x_0$ |
| 解析解 | $x(t)=\frac{K}{1+\left(\frac{K}{x_0}-1\right)e^{-rt}}$ |
| 極限 | $\lim_{t\rightarrow\infty}x(t) = K\left(\mathrm{if}\ r>0\right)$ |
課題1-5:ロジスティックモデルをシミュレーションし、相図を描く¶
def Logistic_ODE(x,r,K,dt):
dx = r*x*(1-x/K)*dt
return x+dx
fig = plt.figure(figsize=(8,4))
ax1 = plt.subplot2grid((1, 4), (0, 0), colspan=3)
ax2 = plt.subplot2grid((1, 4), (0, 3))
r=0.05
K=1
xmin=0; xmax=1.5; xspan=0.1
ax1 = plotVariousInitial(ax1,ODE=Logistic_ODE,xmin=xmin,xmax=xmax,xspan=xspan,r=r,K=K)
ax1.set_title("Logistic model r={}, K={}".format(r,K))
ax1.set_xlabel("Time(t)")
ax1.set_ylabel("Population size (x)")
ax2 = P3_1D(ax2,ODE=Logistic_ODE,xmin=xmin,xmax=xmax,xspan=xspan,r=r,K=K)
plt.tight_layout()
plt.show()
課題1-6:分岐図を描く¶
平衡点の安定性は、「平衡点のごく近傍でどのように振る舞うか」を調べれば良いので、テイラー展開によって解析的に求めることができる。
微分方程式を以下のように定義し、平衡点を $x^{\star}$ と置く。(つまり $f(x^{\star})=0$ )
$$\frac{dx}{dt} = f(x)$$ここで、平衡点からのズレを $\Delta x$ とすると、$\Delta x\simeq0$ において、
$$ \begin{aligned} f(x) &= f(x^{\star} + \Delta x)\\&\simeq f(x^{\star}) + \frac{df}{dx}\left(x^{\star}\right)\Delta x\\&=\frac{df}{dx}\left(x^{\star}\right)\Delta x \end{aligned} $$ゆえに、平衡点における微分係数が 正なら不安定(∵誤差が大きくなっていくから)、負なら安定と分かる。
今回のモデルでは、$K=r$ のとき、平衡点は $x=0,x=K=r$ の二つなので、それぞれにおいて考えると、
$$\frac{df}{dx} = r-2x = \begin{cases} r & (x=0)\\-r &(x=r)\end{cases}$$def Logistic_ODE_Keq2r(x,r,dt):
K=r
dx = r*x*(1-x/K)*dt
return x+dx
fig, ax = plt.subplots()
rmin=-0.08;rmax=0.08;rspan=0.01
xmin=-0.05;xmax=0.05;xspan=0.01
ax = plotBifurcationDiagram(ax, ODE=Logistic_ODE_Keq2r, quiver_color="blue",
pmin=rmin,pmax=rmax,pspan=rspan,pname="r",
xmin=xmin,xmax=xmax,xspan=xspan,xname="x")
func1 = lambda x:x; ax = plotFunc2D(func=func1,ax=ax,color="red",label="$x=r$")
func2 = lambda y:0; ax = plotFunc2D(func=func2,ax=ax,color="red",label="$x=0$")
ax.set_title("bifurcation diagram")
ax.set_xlabel("Parameter (r)")
ax.set_ylabel("State variable (x)")
ax.set_xlim(rmin,rmax)
ax.set_ylim(xmin,xmax)
ax.legend()
plt.show()
1.3 二重井戸ポテンシャルの勾配系¶
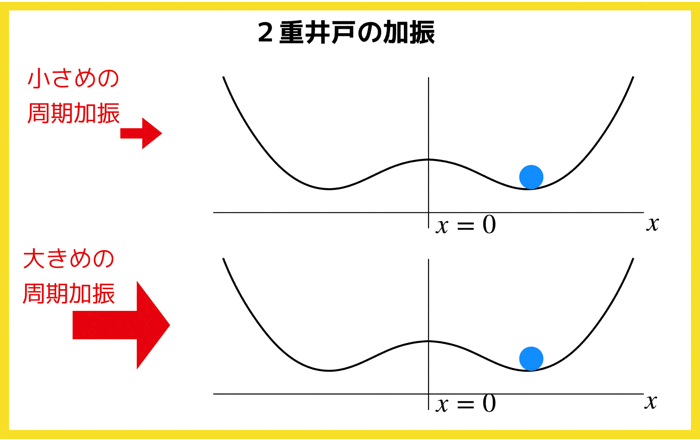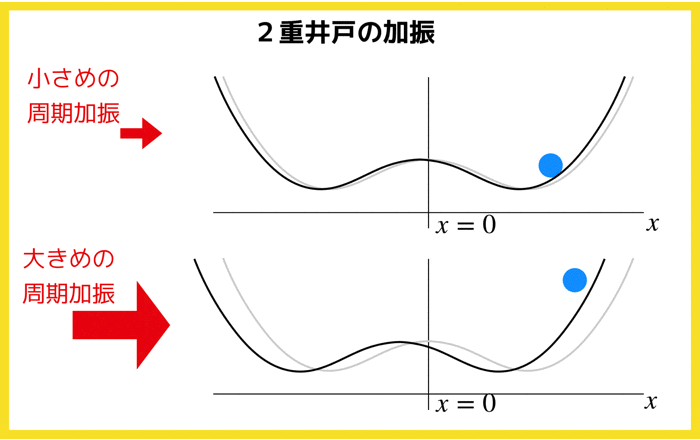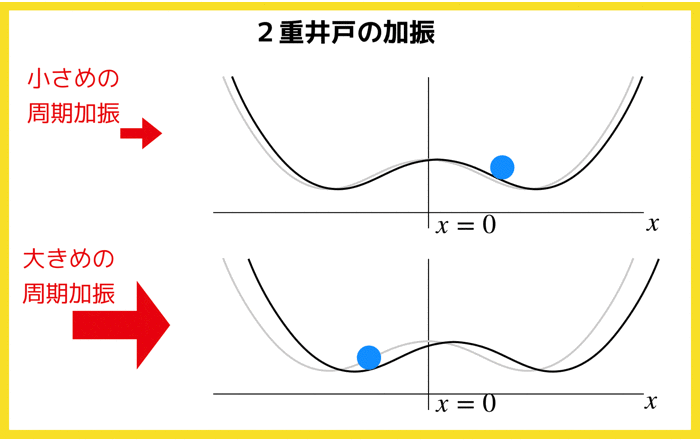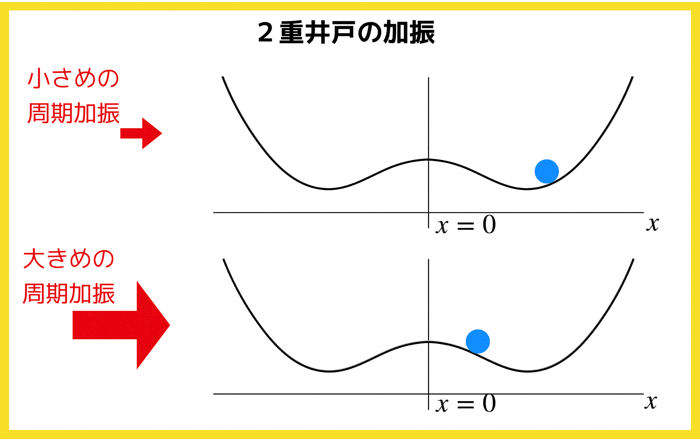
| ポテンシャル | $\phi =\frac{1}{4}x^4 - \frac{1}{2}rx^2$ |
| 微分方程式 | $\frac{dx}{dt} = -\frac{d\phi}{dx} = rx-x^3$ |
| 初期値 | $x(0) = x_0$ |
| 解析解 | $\frac{x^2}{r-x^2} = \frac{x_0^2}{r-x_0^2} e^{2rt}$ |
| 平衡点 | $x=0,x=\pm\sqrt{r}$ |
解析解の求め方¶
$$ \begin{aligned} \frac{dx}{dt} &= rx-x^3 = x\left(r-x^2\right)\\ \int dx\cdot\frac{1}{x}\cdot\frac{1}{\sqrt{r}+x}\cdot\frac{1}{\sqrt{r}-x} &= \int dt\\ \int\left(\frac{1}{r}\cdot\frac{1}{x} - \frac{1}{2r}\frac{1}{\sqrt{r} + x} + \frac{1}{2r}\cdot\frac{1}{\sqrt{r}-x}\right) dx &= \int dt\\ \ln x^2 -\ln\left(\sqrt{r} + x\right) -\ln\left(\sqrt{r} - x\right) &= \int 2rdt\\ \ln\left(\frac{x^2}{r-x^2}\right) &=2rt + C\quad (C\text{: const.})\\ \therefore\ \frac{x^2}{r-x^2} &= \frac{x_0^2}{r-x_0^2} e^{2rt}\\ \end{aligned} $$課題1-7:シミュレーションし、相図を書く¶
def SquareWell_ODE(x,r,dt):
dx = (r*x - x**3) * dt
return x+dx
fig = plt.figure(figsize=(8,6))
xmin=-1.5;xmax=1.5;xspan=0.1
rRange = [-0.5,0.5]
for i,r in enumerate(rRange):
ax1 = plt.subplot2grid((2, 4), (i, 0), colspan=3)
ax2 = plt.subplot2grid((2, 4), (i, 3))
ax1 = plotVariousInitial(ax1,ODE=SquareWell_ODE,xmin=xmin,xmax=xmax,xspan=xspan,r=r,max_t=10)
ax1.set_title("Square Well model r={}".format(r))
ax1.set_xlabel("Time(t)")
ax1.set_ylabel("Ball position (x)")
ax2 = P3_1D(ax2,ODE=SquareWell_ODE,r=r,xmin=xmin,xmax=xmax,xspan=xspan)
plt.tight_layout()
plt.show()
課題1-8:分岐図を描く¶
fig, ax = plt.subplots()
rmin=-1;rmax=2;rspan=0.2
xmin=-1.5;xmax=1.5;xspan=0.1
ax = plotBifurcationDiagram(ax,ODE=SquareWell_ODE,quiver_color="blue",
pmin=rmin,pmax=rmax,pspan=rspan,pname="r",
xmin=xmin,xmax=xmax,xspan=xspan,xname="x")
func1 = lambda x:0; ax = plotFunc2D(func=func1,ax=ax,color="red", label="$x=0$",xmin=rmin,xmax=rmax,xspan=rspan)
func2 = lambda y:y**2; ax = plotFunc2D(func=func2,reverse=True,ax=ax,color="red",label="$r=x^2$",xmin=xmin,xmax=xmax,xspan=xspan)
ax.set_title("bifurcation diagram")
ax.set_xlabel("Parameter (r)")
ax.set_ylabel("State variable (x)")
ax.set_xlim(rmin,rmax)
ax.set_ylim(xmin,xmax)
ax.legend()
plt.show()
全部まとめると…¶
def SquareWell_Potential(x,r):
return 1/4 * x**4 - 1/2 * r * x**2
fig = plt.figure(figsize=(16,8))
xmin=-1.5;xmax=1.5;xspan=0.1
rmin=-1.0;rmax=2.0;rspan=0.2
rRange = [-0.5,0.5]
stabilities = [[(0,0,True)],[(np.sqrt(0.5),-1/16,True),(-np.sqrt(0.5),-1/16,True),(0,0,False)]]
for i,r in enumerate(rRange):
ax1 = plt.subplot2grid((4, 12), (0, 8*i), colspan=4,rowspan=2)
ax2 = plt.subplot2grid((4, 12), (2, 8*i), colspan=3,rowspan=2)
ax3 = plt.subplot2grid((4, 12), (2, 8*i+3), rowspan=2)
ax1 = plotFunc2D(func=SquareWell_Potential, ax=ax1, r=r, color="black", xmin=xmin,xmax=xmax,xspan=xspan)
ax1.set_title("Potential func r={}".format(r))
ax1.set_xlabel("Ball position (x)")
for x,y,flag in stabilities[i]:
ax1 = plotStability(ax1,x,y,flag,text=False)
ax2 = plotVariousInitial(ax2,ODE=SquareWell_ODE,xmin=xmin,xmax=xmax,xspan=xspan,r=r,max_t=10)
ax2.set_title("Square Well position track r={}".format(r))
ax2.set_xlabel("Time(t)")
ax2.set_ylabel("Ball position (x)")
ax3 = P3_1D(ax3,ODE=SquareWell_ODE,r=r,xmin=xmin,xmax=xmax,xspan=xspan)
ax = plt.subplot2grid((4, 12), (1, 4), colspan=4,rowspan=2)
ax = plotBifurcationDiagram(ax, ODE=SquareWell_ODE,quiver_color="blue",
pmin=rmin,pmax=rmax,pspan=rspan,pname="r",
xmin=xmin,xmax=xmax,xspan=xspan,xname="x")
func1 = lambda x:0; ax = plotFunc2D(func=func1,ax=ax,color="red", label="$x=0$",xmin=rmin,xmax=rmax,xspan=rspan)
func2 = lambda y:y**2; ax = plotFunc2D(func=func2,reverse=True,ax=ax,color="red",label="$r=x^2$",xmin=xmin,xmax=xmax,xspan=xspan)
ax.set_title("bifurcation diagram")
ax.set_xlabel("Parameter (r)")
ax.set_ylabel("State variable (x)")
ax.set_xlim(rmin,rmax)
ax.set_ylim(xmin,xmax)
ax.legend()
plt.tight_layout()
plt.show()
よもやま話
ワディントン地形は勾配系における「ポテンシャル」に対応すると考えられる。 しかし、すべての力学系が勾配系として表現できるわけではない。
(つまり、すべての力学系にポテンシャルが存在するわけではない)
それでも、同じ分岐の仕方をする力学系は、分岐点周辺で同じ標準形に近似できる。
2. Notch-Deltaの側方抑制モデル
Notch-Deltaの側方抑制モデル¶
隣り合う細胞がお互いを抑える系は、以下のようにモデル化できる。
| 微分方程式 | $\frac{dx_1}{dt} = a\frac{K^h}{K^h + \left(I\cdot x_2\right)^h}-bx_1$ $\frac{dx_2}{dt} = a\frac{K^h}{K^h + \left(I\cdot x_1\right)^h}-bx_2$ |
| $x_i$ | 細胞 $i$ のDelta濃度 |
| $I$ | 細胞間相互作用の強さ |
| $a,b,K,h$ | パラメータ |
課題2-1:ODEシミュレーション¶
def Notch_Delta_ODE(x1,x2,I,dt,a=1,b=0.5,K=1,h=4):
dx1 = ( a*(K**h / ((K**h) + (I*x2)**h)) - b*x1 ) * dt
dx2 = ( a*(K**h / ((K**h) + (I*x1)**h)) - b*x2 ) * dt
return x1+dx1,x2+dx2
# これでもプロットできるが、ごっちゃになって見づらい…
ax = plotVariousInitial(ax,ODE=Notch_Delta_ODE,xmin=xmin,xmax=xmax,xspan=xspan,max_t=10,otherval=[1],plotall=True,colors=["red","blue"],I=0.4,a=1,b=0.5,K=1,h=4)
Is = [0.4,1]
X1s = [0.5 , 0.75, 1, 1.25, 1.5]
fig = plt.figure(figsize=(16,4))
for r,I in enumerate(Is):
for c,x1 in enumerate(X1s):
ax = fig.add_subplot(len(Is),len(X1s),r*len(X1s)+c+1)
time,res = simulation(ODE=Notch_Delta_ODE,vals=(x1,1),I=I,a=1,b=0.5,K=1,h=4,max_t=10)
ax.plot(time,res[:,0],color="red", label="Cell 1(x1)")
ax.plot(time,res[:,1],color="blue",label="Cell 2(x2)")
ax.set_title("Notch-Delta model x1(0)={},I={}".format(x1,I))
ax.set_xlabel("Time (t)")
ax.set_ylabel("Delta expression")
ax.legend()
plt.tight_layout()
plt.show()
細胞間相互作用が強い時に「分化」が起きる!
課題2-2:分岐図の作成¶
- 2変数あるが、片方の変数 $(x_1)$ にのみ着目する。
- 様々な初期値でODEを解いて、平衡点を見つけ出す。
fig = plt.figure(figsize=(16,8))
Is = [0.4,1]
X1s = [1.5,1,0.5]
for r,I in enumerate(Is):
for c,x1 in enumerate(X1s):
ax = plt.subplot2grid((3, 4), (c, 3*r))
time,res = simulation(ODE=Notch_Delta_ODE,vals=(x1,1),I=I,a=1,b=0.5,K=1,h=4,max_t=10)
ax.plot(time,res[:,0],color="red", label="Cell 1(x1)")
ax.plot(time,res[:,1],color="blue",label="Cell 2(x2)")
ax.set_title("Notch-Delta model x1(0)={},I={}".format(x1,I))
ax.set_xlabel("Time (t)")
ax.set_ylabel("Delta expression")
ax.legend()
Imin=0.4;Imax=1;Ispan=0.05
xmin=0;xmax=2;xspan=0.5
ax = plt.subplot2grid((3, 4), (1, 1), rowspan=2,colspan=2)
ax.scatter(0.5,1.5,marker="o", color='white', edgecolors='black', s=1500)
ax = plotFinalState(ax, ODE=Notch_Delta_ODE,
pmin=Imin,pmax=Imax,pspan=Ispan,pname="I",
xmin=xmin,xmax=xmax,xspan=xspan,xname="x1",
otherstates=[1],xindex=0,
a=1,b=0.5,K=1,h=4,
color="red")
ax.annotate("Which branch to go to fix \ndepends on the noise",(0.5,1.5),textcoords="offset points",xytext=(10,0),size=15)
# ax = plotBifurcationDiagram(ax, ODE=Notch_Delta_ODE, quiver_color="blue",
# pmin=Imin,pmax=Imax,pspan=Ispan,pname="I",
# xmin=xmin,xmax=xmax,xspan=xspan,xname="x1",xindex=0,
# x2=1,a=1,b=0.5,K=1,h=4)
ax.set_title('The relationship between\n"Final state of cell 1 (x1)" and "Cell-cell interaction (I)"')
ax.set_xlabel("Cell-cell interaction (I)")
ax.set_ylabel("Final state of cell 1 (x1)")
ax.set_xlim(Imin,Imax)
ax.set_ylim(xmin,xmax)
plt.tight_layout()
plt.show()
細胞間相互作用を強くしていくと、超臨界ピッチフォーク分岐が起こることが分かる。
In bifurcation theory, a field within mathematics, a pitchfork bifurcation is a particular type of local bifurcation where the system transitions from one fixed point to three fixed points. (Wikipedia)
3. LacYのポジティブ・フィードバックモデル
LacYのポジティブフィードバックモデル¶
大腸菌は、ラクトースを積極的に利用するが、その様子は以下のようにモデル化できる。
| 微分方程式 | $$\begin{aligned} \frac{\mathrm{d} x}{\mathrm{d} t} &=-x+\alpha X_{o u t}+\beta y \\ \frac{\mathrm{d} y}{\mathrm{d} t} &=\frac{x^{2}}{\rho+x^{2}}-y \end{aligned}$$ |
| $x$ | 細胞内TMG濃度 |
| $y$ | LacY-GFP濃度 |
| $X_{out}$ | 細胞外TMG濃度 |
| $\alpha,\beta$ | Rate constants |
| $\rho$ | Tightness of LacⅠ repression |
| イメージ |  |
課題3-1:パラメータと初期値を変えてシミュレーション¶
def Ozbudak_ODE(x,y,alpha=0.1,beta=9.5,rho=25,x_out=5,hill=2,dt=0.01):
dx = (-x + alpha*x_out + beta*y) * dt
dy = (x**hill/(rho+x**hill) - y) * dt
return x+dx,y+dy
iniYs = [0,0.33,0.67,1]
Xouts = [10,5,0]
x = 0
fig = plt.figure(figsize=(16,8))
for r,x_out in enumerate(Xouts):
for c,y in enumerate(iniYs):
ax = fig.add_subplot(len(Xouts),len(iniYs),r*len(iniYs)+c+1)
time,res = simulation(ODE=Ozbudak_ODE,vals=(x,y),alpha=0.1,beta=9.5,rho=25,x_out=x_out,hill=2,max_t=100)
ax.plot(time,res[:,0],color="red", label="TMGin(x)")
ax.plot(time,res[:,1],color="blue",label="LacY(y)")
ax.set_title("$X_{out}="+"{},y(0)={}$".format(x_out,y))
ax.set_xlabel("Time(t)")
ax.set_ylabel("Concentration")
ax.set_xlim(0,100)
ax.set_ylim(0,10)
ax.legend()
plt.tight_layout()
plt.show()
細胞外TMGが中間の時だけ双安定性を示すことがわかる。なお、
- 大きい時($X_{out}=10$)は単安定(高いモード)
- 中間の時($X_{out}=5$)は双安定
- 小さい時($X_{out}=0$)は単安定(低いモード) </b>
課題3-2:分岐図の作成¶
- (数値解)本当は二次元の連立微分方程式だが、片方の変数($y$)のみに注目し、もう片方の変数($x$)は固定($x=0$)
- (数値解)様々な初期値でODEをといて、平衡点を見つけ出す。(「$t\rightarrow\infty$ で収束する点が平衡点」としている)
- (解析解)代数的に連立微分方程式を解いて平衡点を探す。
import sympy
colors = [
[0.32156863, 1. , 0.32156863, 0.5],
[0.97647059, 0.34901961, 0.97647059, 0.5],
[1. , 0.88627451, 0.18823529, 0.5],
[0.35686275, 0.36078431, 1. , 0.5]
]
xout_y = [(5,0.67),(10,1),(0,0),(5,0.33)]
yfinals = [0.6208191139095129,0.701415737056882,0.0,0.01739404337057098]
alpha=0.1; beta=9.5; rho=25;
xoutmin=0;xoutmax=10;xoutspan=0.5
Xouts = np.arange(xoutmin,xoutmax+xoutspan,xoutspan)
fig = plt.figure(figsize=(8,12))
#=== Outside plots ===
x=0
for c in range(2):
for r in range(2):
ax = plt.subplot2grid((4, 2), (r*3, c))
ax.set_facecolor(colors[r*2+c])
x_out,y = xout_y[r*2+c]
time,res = simulation(ODE=Ozbudak_ODE,vals=(x,y),alpha=alpha,beta=beta,rho=rho,x_out=x_out,hill=2,max_t=100)
ax.plot(time,res[:,0],color="red", label="TMGin(x)")
ax.plot(time,res[:,1],color="blue",label="LacY(y)")
ax.set_title("$X_{out}="+"{},y(0)={}$".format(x_out,y))
ax.set_xlabel("Time(t)")
ax.set_ylabel("Concentration")
ax.set_xlim(0,100)
ax.set_ylim(0,10)
ax.legend()
#=== Center plots ===
# Characteristic four points (color squares)
ax = plt.subplot2grid((4, 2), (1, 0), colspan=2,rowspan=2)
for c in range(2):
for r in range(2):
ax.scatter(xout_y[r*2+c][0],yfinals[r*2+c], marker="s", color='white', edgecolors=colors[r*2+c], s=1000,linewidths=3)
# unstable point cercles
ax.scatter(7,0.1,marker="o", color='white', edgecolors='black', s=3000)
ax.scatter(2.5,0.48,marker="o", color='white', edgecolors='black', s=3000)
# Analytical plots(×)
x = sympy.Symbol('x')
y = sympy.Symbol('y')
for x_out in Xouts:
#=== solve the simultaneous differential equations ===
ODE1 = -x + alpha*x_out + beta*y
ODE2 = x**2/(rho+x**2) - y
for xy in sympy.solve([ODE1, ODE2]):
if xy[y].is_complex:
# Handling numerical errors
if abs(sympy.im(xy[y])) < 1e-10:
ax.scatter(x_out, float(sympy.re(xy[y])), marker="o", color='white', edgecolors='black', s=100)
else:
ax.scatter(x_out, float(xy[y]), marker="o", color='white', edgecolors='black', s=100)
# Numerical plots(◯)
x=0
ymin=0;ymax=1;yspan=0.1
ax = plotFinalState(ax, ODE=Ozbudak_ODE,
pmin=xoutmin,pmax=xoutmax,pspan=xoutspan,pname="x_out",
xmin=ymin, xmax=ymax, xspan=yspan, xname="y",
otherstates=[x],xindex=1,
alpha=alpha,beta=beta,rho=rho,hill=2,
color="red")
# Add labels
ax.scatter(0,0,marker="o", color='white', edgecolors='black', s=100, label="Analytical")
ax.scatter(0,0,marker="x",color="red", label="Numerical($x={}$)".format(x))
ax.set_title('The relationship between\n"Final state of LacY-GFP (y)" and "TMGout (Xout)"')
ax.set_xlabel("TMGout (Xout)")
ax.set_ylabel("Final state of LacY-GFP (y)")
ax.legend()
plt.tight_layout()
plt.show()
ある$X_{out}$ に対して、安定平衡点(×)と不安定平衡点(◯のみ、解析的にしか現れず、ほとんどの初期値で到達できない平衡点)があることから、サドルノード分岐をしていることがわかる。
サドルノード分岐
サドル(不安定平衡点)とノード(安定平衡点)が対生成あるいは対消滅する分岐。
分岐図から予測できること¶
また、上記の分岐図から、$\mathrm{TMG_{out}}$ を上げていく時と $\mathrm{TMG_{out}}$ を下げていく時で別の経路を辿っていく、つまり、ヒステリシス(履歴依存性がある)と考えられる。2018年のDay5 課題3で実際にプロットしている。
実験的な操作としては以下に対応する。
- $\mathrm{TMG}=\mathrm{X\ \mu M}$ で培養
- 集菌($x$ がリセットされ、$y$ は保存される。)
- $\mathrm{TMG}=\mathrm{\left(X\pm\Delta X\right)\ \mu M}$ で培養
- 以降上記操作の繰り返し
課題3-3:シミュレーションで $\mathrm{TMG_{out}}$ を時間変化させよ¶
$X_{out}$ をステップ状に変化させた時の $y$ の最終値を観察しよう。
こちらも2018年のDay5 課題2でプロットしているので割愛する。
4. (発展課題)解糖系振動のモデル
力学系の安定な状態は、「(平衡)点」とは限らず、「安定な振動現象」も存在する。これらも全て2018年のDay5でプロットしているので割愛する。
| Name | 由来 |
|---|---|
| Sel'kov | 解糖系 |
| FitzHugh-Nagumo | 神経発火 |
| Repressilator | 合成生物学 |
</b>
And more...¶
さらに力学系を深く理解したい場合は、以下の本がおすすめとのこと。
| Hirsch・Smale・Devaney 力学系入門 ―微分方程式からカオスまで | ストロガッツ 非線形ダイナミクスとカオス |
|---|---|
 |
 |