今回の講義は今までの復習であり、隠れマルコフモデルについて結構重点的に触れたので、Baum-Welch アルゴリズムを用いて隠れマルコフモデルのパラメータを推定し、Viterbi アルゴリズムを用いて最大系列を推定するプログラムを Python で実行して理解を深めます。なお、以下の説明で用いられている式番号はPRMLに基づいています。
Python のコードだけ知りたい方は、ここまで飛ばしてください。
隠れマルコフモデル(hidden Markov model, HMM)¶
隠れマルコフモデルに従う観測データ $\{\mathbf{x}_n\}$ と隠れ変数 $\{\mathbf{z}_n\}$ の同時分布は以下のようになります。 $$p(\mathbf{X}, \mathbf{Z} | \boldsymbol{\theta})=p\left(\mathbf{z}_{1} | \boldsymbol{\pi}\right)\left[\prod_{n=2}^{N} p\left(\mathbf{z}_{n} | \mathbf{z}_{n-1}, \mathbf{A}\right)\right] \prod_{m=1}^{N} p\left(\mathbf{x}_{m} | \mathbf{z}_{m}, \boldsymbol{\phi}\right)\qquad (13.10)$$ したがって、均一マルコフ連鎖(斉次モデル)であれば、以下の三種類のパラメータ $\{\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}\} = \boldsymbol{\theta}$ が必要となります。
- 初期状態(initial state): $p(\mathbf{z}_1)$ を記述するパラメータ $\boldsymbol{\pi}$
- 遷移確率(transition probability): $p(\mathbf{z}_n|\mathbf{z}_{n-1})$ を記述するパラメータ $\mathbf{A}$
- 出力確率(emission probability): $p(\mathbf{x}_n|\mathbf{z}_n)$ を記述するパラメータ $\boldsymbol{\phi}$
最初の潜在ノード $\mathbf{z}_1$ は、要素 $\pi_k\equiv p(z_{1 k} = 1)$ をもつ確率のベクトル $\boldsymbol{\pi}$ で表される周辺分布 $p(\mathbf{z}_1)$ を持ちます。 $$p\left(\mathbf{z}_{1} | \boldsymbol{\pi}\right)=\prod_{k=1}^{K} \pi_{k}^{z_{1 k}}\qquad (13.8)$$ 遷移確率は、$A_{j k}\equiv p(z_{n k} = 1|z_{n-1,j} = 1)$ で定義されるので、以下のように書けます。 $$p\left(\mathbf{z}_{n} | \mathbf{z}_{n-1, \mathbf{A}}\right)=\prod_{k=1}^{K} \prod_{j=1}^{K} A_{j k}^{z_{n-1, j} z_{n k}}\qquad (13.7)$$ 放出確率はどのような分布も考えることができます。$z_n = k$ の場合の分布のパラメータを $\phi_k$ とすれば、以下の形で書くことができます。 $$p\left(\mathbf{x}_{n} | \mathbf{z}_{n}, \boldsymbol{\phi}\right)=\prod_{k=1}^{K} p\left(\mathbf{x}_{n} | \boldsymbol{\phi}_{k}\right)^{z_{n k}}\qquad (13.9)$$
Baum-Welch algorithm¶
データ集合 $\mathbf{X} = \{\mathbf{x}_1,\ldots,\mathbf{x}_N\}$ が観測された場合、HMMのパラメータを最尤推定で決定することができます。
同時分布の式
$$p(\mathbf{X}, \mathbf{Z} | \boldsymbol{\theta})=p\left(\mathbf{z}_{1} | \boldsymbol{\pi}\right)\left[\prod_{n=2}^{N} p\left(\mathbf{z}_{n} | \mathbf{z}_{n-1}, \mathbf{A}\right)\right] \prod_{m=1}^{N} p\left(\mathbf{x}_{m} | \mathbf{z}_{m}, \boldsymbol{\phi}\right)\qquad (13.10)$$
を潜在変数について周辺化することで、以下の尤度関数が得られます。
$$p(\mathbf{X} | \boldsymbol{\theta})=\sum_{\mathbf{Z}} p(\mathbf{X}, \mathbf{Z} | \boldsymbol{\theta})\qquad (13.11)$$
ここで、同時分布 $p(\mathbf{X} | \boldsymbol{\theta})$ は $n$ について分解することができないので、各々の $\mathbf{z}_n$ に関する和を独立なものとして単純に扱うことができません。
さらに、和を取る対象が $N$ 個の変数で、その各々が $K$ 状態を取る結果、全部で $K^N$ 項になり、明示的に和の演算を実行することもできません。
また、尤度関数(13.11)におけるさらなる困難は、混合分布の一般化に相当しているために、潜在変数の異なる値に対する出力モデルの和になっている点です。そのため、尤度関数を直接最大化しようとすると、閉じた形の解を持たない複雑な式になってしまいます。
そこで、ここでは、隠れマルコフモデルの尤度関数を最大化する効率的な枠組みとして、Baum-Welchアルゴリズムを考えることにします。なお、これは機械学習の分野でよく使われるEMアルゴリズムの一種です。
$Q$ 関数¶
Eステップでは、パラメータ $\boldsymbol{\theta}$ の値を利用して、潜在変数 $p(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{\mathrm{old}})$ の事後分布を求めます。
次に、この事後分布を用いて、パラメータ集合 $\boldsymbol{\theta}$ の関数としての、データに対する尤度関数の対数の期待値を求めます。この期待値は、以下の関数 $Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{\text { old }}\right)$ で定義されます。
$$Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{\text { old }}\right)=\sum_{\mathbf{Z}} p(\mathbf{Z} | \mathbf{X}, \boldsymbol{\theta}^{\text { old }}) \ln p(\mathbf{X}, \mathbf{Z} | \boldsymbol{\theta})\qquad (13.12)$$
ここで、表記を簡単にするため、いくつかの記号を導入します。
これらを用いることで、Eステップで最大化したい $Q$ 関数が以下のように表されます。 $$\begin{aligned} Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{\text { old }}\right) =& \sum_{k=1}^{K} \gamma\left(z_{1 k}\right) \ln \pi_{k}+\sum_{n=2}^{N} \sum_{j=1}^{K} \sum_{k=1}^{K} \xi\left(z_{n-1, j}, z_{n k}\right) \ln A_{j k} \\ & +\sum_{n=1}^{N} \sum_{k=1}^{K} \gamma\left(z_{n k}\right) \ln p\left(\mathbf{x}_{n} | \boldsymbol{\phi}_{k}\right)\qquad (13.17) \end{aligned}$$
M step¶
Mステップでは、$\gamma(\mathbf{z}),\xi(\mathbf{z}_{n-1},\mathbf{z})$ を定数とみなし、パラメータ $\boldsymbol{\theta} = \{\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}\}$ に関して $Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{\text { old }}\right)$ を最大化します。
ただし、$\boldsymbol{\pi},\mathbf{A}$ には制約条件が付くので、ラグランジュの未定乗数を導入して、以下の式を解く必要があります。
$$\begin{aligned}
&Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{\text { old }}\right)
=\sum_{k=1}^{K} \gamma\left(z_{1 k}\right) \ln \pi_{k}+\sum_{n=2}^{N} \sum_{j=1}^{K} \sum_{k=1}^{K} \xi\left(z_{n-1, j}, z_{n k}\right) \ln A_{j k} \\
& +\sum_{n=1}^{N} \sum_{k=1}^{K} \gamma\left(z_{n k}\right) \ln p\left(\mathbf{x}_{n} | \boldsymbol{\phi}_{k}\right) + \lambda_1\left(\sum_{k=1}^K\pi_k - 1\right) + \sum_{j=1}^K\lambda_{2,j}\left(\sum_{k=1}^K A_{jk} - 1\right)
\end{aligned}$$
難しく見えますが、$\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}$ を含む項は別々になっているので、計算は楽です。
$\boldsymbol{\pi}$ に関する最大化¶
以下を $\boldsymbol{\pi}$ に関して最大化すれば良いです。 $$Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{\text { old }}\right) = \sum_{k=1}^{K} \gamma\left(z_{1 k}\right) \ln \pi_{k} + \lambda_1\left(\sum_{k=1}^K\pi_k - 1\right)$$ したがってこれは簡単に求まり、 $$\pi_{k}=\frac{\gamma\left(z_{1 k}\right)}{\sum_{j=1}^{K} \gamma\left(z_{1 j}\right)}\qquad (13.20)$$ となります。
$\mathbf{A}$ に関する最大化¶
同様に、以下を $\mathbf{A}$ に関して最大化すれば良いです。 $$\begin{aligned} Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{\text { old }}\right) & = \sum_{n=2}^{N} \sum_{j=1}^{K} \sum_{k=1}^{K} \xi\left(z_{n-1, j}, z_{n k}\right) \ln A_{j k}\\ & + \sum_{j=1}^K\lambda_{2,j}\left(\sum_{k=1}^K A_{jk} - 1\right) \end{aligned}$$ これも簡単に求まり、以下を得ます。 $$A_{j k}=\frac{\sum_{n=2}^{N} \xi\left(z_{n-1, j}, z_{n k}\right)}{\sum_{l=1}^{K} \sum_{n=2}^{N} \xi\left(z_{n-1, j}, z_{n l}\right)}\qquad (13.19)$$
$\phi_k$ に関する最大化¶
$Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{\text { old }}\right)$ を $\phi_k$ に関して最大化する場合、以下を $\phi_k$ に関して最大化すれば良いことがわかります。 $$Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{\text { old }}\right) = \sum_{n=1}^{N} \sum_{k=1}^{K} \gamma\left(z_{n k}\right) \ln p\left(\mathbf{x}_{n} | \boldsymbol{\phi}_{k}\right)$$ これは、$\gamma(z_{n k})$ が負担率の役割を果たす標準的な混合分布に対する $Q$ 関数のデータ依存項と全く同一です。したがって、重み $\gamma_{n k}$ で重み付けられた出力確率 $p(\mathbf{x}|\phi_k)$ の重み付き対数尤度関数を単に最大化すれば良くなります。 例えば出力分布がガウス密度関数の時($p(\mathbf{x}|\phi_k) = \mathcal{N}(\mathbf{x}|\boldsymbol{\mu}_k,\boldsymbol{\Sigma}_k)$)には以下を得ます。 $$\begin{aligned} \boldsymbol{\mu}_{k} & =\frac{\sum_{n=1}^{N} \gamma\left(z_{n k}\right) \mathbf{x}_{n}}{\sum_{n=1}^{N} \gamma\left(z_{n k}\right)} & (13.20)\\ \Sigma_{k} & =\frac{\sum_{n=1}^{N} \gamma\left(z_{n k}\right)\left(\mathrm{x}_{n}-\mu_{k}\right)\left(\mathrm{x}_{n}-\mu_{k}\right)^{\mathrm{T}}}{\sum_{n=1}^{N} \gamma\left(z_{n k}\right)} & (13.21) \end{aligned}$$
E step¶
それでは、EMアルゴリズムのEステップで $\gamma(z_{n k}),\xi(z_{n-1,j},z_{n k})$ を効率的に求めるアルゴリズムを検討します。
HMMのグラフは木構造をもちます。したがって、二段階のメッセージパッシングアルゴリズムをによって潜在変数の事後確率 $\gamma_{n k}$ を効率良く求めることができます。これを、フォワード-バッグワードアルゴリズム(forward-backward algorithm)やBaum-Welchアルゴリズムと呼びます。
まず、ベイズの定理より以下が成立するので、
$$\gamma\left(\mathbf{z}_{n}\right)=p\left(\mathbf{z}_{n} | \mathbf{X}\right)=\frac{p(\mathbf{X} | \mathbf{z}_{n}) p\left(\mathbf{z}_{n}\right)}{p(\mathbf{X})}\qquad (13.32)$$
$\boldsymbol{\theta}^{\mathrm{old}}$ を使って $p(\mathbf{x}|\mathbf{z}_n)$ を計算することができれば $\gamma_{n k}$ を求めることができます。
ここで、$z_n$ の値が定まると $n$ より過去より未来が独立になるので、
$$p(\mathbf{X} | \mathbf{z}_{n})= p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n} | \mathbf{z}_{n}\right)p\left(\mathbf{x}_{n+1}, \ldots, \mathbf{x}_{N} | \mathbf{z}_{n}\right)$$と分解ができます。
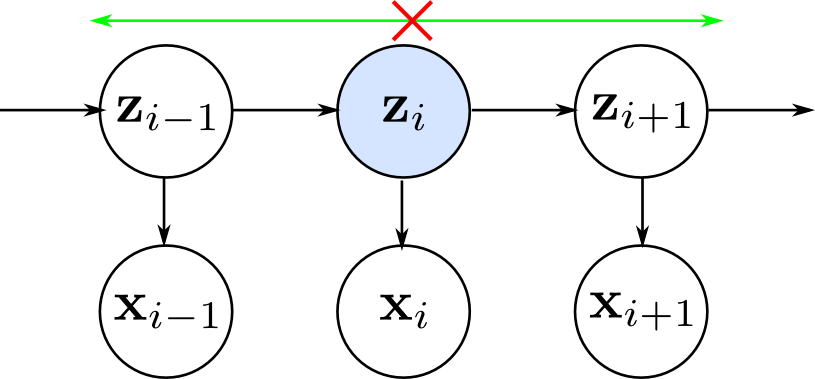これと $p(\mathbf{x}_1,\ldots,\mathbf{x}_n|z_n)p(z_n) = p(\mathbf{x}_1,\ldots,\mathbf{x}_n,z_n)$ であることを利用すれば、
$$\gamma_{n k} = p(\mathbf{z}_n|\mathbf{x}) = \frac{p(\mathbf{x}_1,\ldots,\mathbf{x}_n,\mathbf{z}_n)p(\mathbf{x}_{n+1},\ldots,\mathbf{x}_N|\mathbf{z}_n)}{p(\mathbf{x})}$$
と表すことができます。そこで、
$$\begin{aligned}
\alpha(\mathbf{z}_n)
& = p(\mathbf{x}_1,\ldots,\mathbf{x}_n,\mathbf{z}_n)
& (13.34)\\
\beta(z_i)
& = p(\mathbf{x}_{n+1},\ldots,\mathbf{x}_N|\mathbf{z}_n)
& (13.35)
\end{aligned}$$
と定義します。これらを用いれば、
$$\gamma\left(\mathbf{z}_{n}\right)=\frac{p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n}, \mathbf{z}_{n}\right) p\left(\mathbf{x}_{n+1}, \ldots, \mathbf{x}_{N} | \mathbf{z}_{n}\right)}{p(\mathbf{X})}
=\frac{\alpha\left(\mathbf{z}_{n}\right) \beta\left(\mathbf{z}_{n}\right)}{p(\mathbf{X})}\qquad (13.33)$$
のように表すことができます。
ここで目的となるのは、$\alpha$ の漸化式を求めること（前向き）と $\beta$ の漸化式を求めること（後ろ向き）です。
前向き¶
条件付き独立性や加法・乗法定理を用いることで、以下のように $\alpha(\mathbf{z}_{n-1})$ を用いて $\alpha(\mathbf{z}_n)$ を表すことが可能になります。 $$\begin{aligned} \alpha\left(\mathbf{z}_{n}\right) & =p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n}, \mathbf{z}_{n}\right) \\ & =p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n} | \mathbf{z}_{n}\right) p\left(\mathbf{z}_{n}\right) \\ & =p\left(\mathbf{x}_{n} | \mathbf{z}_{n}\right) p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n-1} | \mathbf{z}_{n}\right) p\left(\mathbf{z}_{n}\right) \\ & =p\left(\mathbf{x}_{n} | \mathbf{z}_{n}\right) p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n-1}, \mathbf{z}_{n}\right) \\ & =p\left(\mathbf{x}_{n} | \mathbf{z}_{n}\right) \sum_{\mathbf{z}_{n-1}} p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n-1}, \mathbf{z}_{n-1}, \mathbf{z}_{n}\right) \\ & =p\left(\mathbf{x}_{n} | \mathbf{z}_{n}\right) \sum_{\mathbf{z}_{n-1}} p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n-1}, \mathbf{z}_{n} | \mathbf{z}_{n-1}\right) p\left(\mathbf{z}_{n-1}\right) \\ & =p\left(\mathbf{x}_{n} | \mathbf{z}_{n}\right) \sum_{\mathbf{z}_{n-1}} p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n-1} | \mathbf{z}_{n-1}\right) p\left(\mathbf{z}_{n} | \mathbf{z}_{n-1}\right) p\left(\mathbf{z}_{n-1}\right) \\ & =p\left(\mathbf{x}_{n} | \mathbf{z}_{n}\right) \sum_{\mathbf{z}_{n-1}} p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n-1}, \mathbf{z}_{n-1}\right) p\left(\mathbf{z}_{n} | \mathbf{z}_{n-1}\right) \\ & =p\left(\mathbf{x}_{n} | \mathbf{z}_{n}\right) \sum_{\mathbf{z}_{n-1}} \alpha(\mathbf{z}_{n-1})p(\mathbf{z} | \mathbf{z}_{n-1})\\ \end{aligned}$$
よって、再帰式は、以下のようになります。 $$\alpha\left(\mathbf{z}_{n}\right)=p\left(\mathbf{x}_{n} | \mathbf{z}_{n}\right) \sum_{\mathbf{z}_{n-1}} \alpha\left(\mathbf{z}_{n-1}\right) p\left(\mathbf{z}_{n} | \mathbf{z}_{n-1}\right)\qquad (13.36)$$ この再帰を開始するためには、以下で与えられる初期条件が必要になります。 $$\alpha\left(\mathbf{z}_{1}\right)=p\left(\mathbf{x}_{1}, \mathbf{z}_{1}\right)=p\left(\mathbf{z}_{1}\right) p\left(\mathbf{x}_{1} | \mathbf{z}_{1}\right)=\prod_{k=1}^{K}\left\{\pi_{k} p\left(\mathbf{x}_{1} | \boldsymbol{\phi}_{k}\right)\right\}^{z_{1 k}}\qquad (13.37)$$ 再帰の各段階が $K\times K$ 行列による乗算を含むので、鎖全体に対してこれらの値を求める全体のコストは $\mathcal{O}(K^2N)$ になります。
意味を解釈すると、$(n-1)$ ステップの $\alpha(\mathbf{z}_{n-1})$ の要素 $\alpha(z_{n-1,j})$ について、$p(\mathbf{z}_n|\mathbf{z}_{n-1})$ の値に相当する $A_{j1}$ で与えられる重みを用いて、重み付け和を取り、さらにそれにデータの寄与 $p(\mathbf{x}_n|z_{n1})$ を掛けることで $\alpha(z_{n,1})$ を得ています。
後ろ向き¶
同様にして、$\beta(\mathbf{z}_n)$ に関する再帰式は以下のように定義できます。 $$\begin{aligned} \beta\left(\mathbf{z}_{n}\right) & =p\left(\mathbf{x}_{n+1}, \ldots, \mathbf{x}_{N} | \mathbf{z}_{n}\right) \\ & =\sum_{\mathbf{z}_{n+1}} p\left(\mathbf{x}_{n+1}, \ldots, \mathbf{x}_{N}, \mathbf{z}_{n+1} | \mathbf{z}_{n}\right) \\ & =\sum_{\mathbf{z}_{n+1}} p\left(\mathbf{x}_{n+1}, \ldots, \mathbf{x}_{N} | \mathbf{z}_{n}, \mathbf{z}_{n+1}\right) p\left(\mathbf{z}_{n+1} | \mathbf{z}_{n}\right) \\ & =\sum_{\mathbf{z}_{n+1}} p\left(\mathbf{x}_{n+1}, \ldots, \mathbf{x}_{N} | \mathbf{z}_{n+1}\right) p\left(\mathbf{z}_{n+1} | \mathbf{z}_{n}\right) \\ & =\sum_{\mathbf{z}_{n+1}} p\left(\mathbf{x}_{n+2}, \ldots, \mathbf{x}_{N} | \mathbf{z}_{n+1}\right) p\left(\mathbf{x}_{n+1} | \mathbf{z}_{n+1}\right) p\left(\mathbf{z}_{n+1} | \mathbf{z}_{n}\right) \\ & =\sum_{\mathbf{z}_{n+1}} \beta(\mathbf{z}_{n+1})p(\mathbf{x}_{n+1}|\mathbf{z}_{n+1})p(\mathbf{z}_{n+1}|\mathbf{z}_n)\qquad (13.38) \end{aligned}$$</p>
ここでの初期条件は、(13.33)で $n=N$ と置くことによって、以下になります。$\mathbf{z}_n$ の全ての値について $\beta(\mathbf{z}_n) = 1$ とすることでこの式は正しくなります。 $$p\left(\mathbf{z}_{N} | \mathbf{X}\right)=\frac{p\left(\mathbf{X}, \mathbf{z}_{N}\right) \beta\left(\mathbf{z}_{N}\right)}{p(\mathbf{X})}\qquad (13.39)$$
こちらも意味を解釈すると、$n+1$ ステップの $\beta(\mathbf{z_{n+1}})$ の要素 $\beta(z_{n+1},k)$ について重み付け和を取ることで、$\beta(z_{n,1})$ を得ます。ここで、各 $\beta(z_{n+1,k})$ に対する重みは、$p(\mathbf{z_{n+1}}|\mathbf{z}_n)$ の値に対応する $A_{1 k}$ とその要素に対応する出力密度 $p(\mathbf{x}_n|z_{n+1,k})$ の値を乗じたものです。
$p(\mathbf{X})$ の計算¶
$p(\mathbf{X})$ は尤度関数を表し、EMアルゴリズムの停止条件などに利用されることがあるのでその値を求めることは有用です。 $$\gamma\left(\mathbf{z}_{n}\right) =\frac{p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n}, \mathbf{z}_{n}\right) p\left(\mathbf{x}_{n+1}, \ldots, \mathbf{x}_{N} | \mathbf{z}_{n}\right)}{p(\mathbf{X})} =\frac{\alpha\left(\mathbf{z}_{n}\right) \beta\left(\mathbf{z}_{n}\right)}{p(\mathbf{X})}\qquad (13.33)$$ の両辺において $\mathbf{z}_n$ について和を取り、左辺が正規化された分布であることを利用すると、 $$p(\mathbf{X})=\sum_{\mathbf{z}_{n}} \alpha\left(\mathbf{z}_{n}\right) \beta\left(\mathbf{z}_{n}\right)\qquad (13.41)$$ が得られます。すなわち、$n$ を好きなように取り、この和を計算することで尤度関数を求めることができます。よって、単に尤度関数を求めたい場合は $n=N$ の結果を用いて、以下で求めることが可能です。 $$p(\mathbf{X})=\sum_{\mathbf{k}_{N}} \alpha\left(\mathbf{z}_{N}\right)\qquad (13.42)$$
$\xi(\mathbf{z}_{n-1},\mathbf{z}_n)$ の計算¶
$(\mathbf{z}_{n-1},\mathbf{z}_n)$ の $K\times K$ 個の値の組各々についての条件付き確率 $p(\mathbf{z}_{n-1},\mathbf{z}_n)$ に対応する $\xi(\mathbf{z}_{n-1},\mathbf{z}_n)$ は、ベイズの定理を用いることによって、以下で表されます。 $$\begin{array}{l} {\xi\left(\mathbf{z}_{n-1}, \mathbf{z}_{n}\right)=p\left(\mathbf{z}_{n-1}, \mathbf{z}_{n} | \mathbf{X}\right)} \\ {=\frac{p(\mathbf{X} | \mathbf{z}_{n-1}, \mathbf{z}_{n}) p\left(\mathbf{z}_{n-1}, \mathbf{z}_{n}\right)}{p(\mathbf{X})}} \\ {=\frac{p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n-1} | \mathbf{z}_{n-1}\right) p\left(\mathbf{x}_{n} | \mathbf{z}_{n}\right) p\left(\mathbf{x}_{n+1}, \ldots, \mathbf{x}_{N} | \mathbf{z}_{n}\right) p\left(\mathbf{z}_{n} | \mathbf{z}_{n-1}\right) p\left(\mathbf{z}_{n-1}\right)}{p(\mathbf{X})}} \\ {=\frac{\alpha\left(\mathbf{z}_{n-1}\right) p\left(\mathbf{x}_{n} | \mathbf{z}_{n}\right) p\left(\mathbf{z}_{n} | \mathbf{z}_{n-1}\right) \beta\left(\mathbf{x}_{n}\right)}{p(\mathbf{X})}} \qquad (13.43) \end{array}$$ したがって、すでに計算した $\alpha(\mathbf{z}_n)$ と $\beta(\mathbf{z}_n)$ の値を用いて更新ができます。
まとめ¶
初期化¶
最初に、パラメータ $\boldsymbol{\theta}^{\mathrm{old}}$ の初期値を求めます。
パラメータ $\mathbf{A}$ や $\boldsymbol{\mu}$ は、一様に、もしくはランダムに、一様分布から非負性や和の制約を満たす範囲内で選択されることが多いです。
パラメータ $\boldsymbol{\phi}$ の初期化は、出力分布の形により異なります。例えば、ガウス分布の場合には、データに K-means アルゴリズムを用いることによって $\boldsymbol{\mu}_k$ が初期化され、$\boldsymbol{\Sigma}_k$ の初期値としては対応する $K$ 個のクラスの共分散行列が用いられることがあります。
Estep¶
まず、フォワード $\alpha$ 再帰とバックワード $\beta$ 再帰が実行され、その結果を用いて $\gamma(\mathbf{z}_n)$ と $\xi(\mathbf{z_{n-1},\mathbf{z}_n})$ を求めることができます。この段階で尤度関数も求めることができます。
Mstep¶
上で求めたパラメータを固定し、 $$\begin{aligned} Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{\text { old }}\right) =& \sum_{k=1}^{K} \gamma\left(z_{1 k}\right) \ln \pi_{k}+\sum_{n=2}^{N} \sum_{j=1}^{K} \sum_{k=1}^{K} \xi\left(z_{n-1, j}, z_{n k}\right) \ln A_{j k} \\ & +\sum_{n=1}^{N} \sum_{k=1}^{K} \gamma\left(z_{n k}\right) \ln p\left(\mathbf{x}_{n} | \boldsymbol{\phi}_{k}\right)\qquad (13.17) \end{aligned}$$ を最大化するようなパラメータ集合 $\boldsymbol{\theta}^{\mathrm{old}}$ を求めます.
停止条件¶
ある収束基準、例えば尤度関数の変化やパラメータの変化がある閾値より小さくなるまで、E step と M step を繰り返します。
Viterbi algorithm¶
隠れマルコフモデルの多くの応用で、潜在変数は何らかの意味を持つと解釈されます。そこで、与えられた観測系列に対し、隠れ状態の最も確からしい系列を求めることにしばしば興味が持たれます。
例えば、遺伝子配列解析で、隠れた状態から配列が決まっていると仮定すれば、その隠れた状態を見つけることに意味があると思われます。
隠れマルコフモデルのグラフは有向木なので、この問題はmax-sumアルゴリズムを用いることで厳密に解くことができます。
ここで、先ほど利用したBaum-Welch(積和)アルゴリズムを用いて単純に潜在変数の周辺確率 $\gamma(\mathbf{z}_n)$ を求め、各 $n$ について最も確からしい状態の集合を求めるだけでは、一般には最も確からしい状態系列に対応しないことに注意が必要です。
この問題の定式化をすると、$\mathbf{Z}$ の事後確率が最大となる系列 $\hat{\mathbf{Z}}$ を見つけるという問題に対応するので、
$$\begin{aligned}
\hat{\mathbf{Z}}
& = \mathop{\rm arg~max}\limits_{\mathbf{Z}}p(\mathbf{Z}|\mathbf{X}) \\
& = \mathop{\rm arg~max}\limits_{\mathbf{Z}}\frac{p(\mathbf{X},\mathbf{Z})}{p(\mathbf{X})} \\
& = \mathop{\rm arg~max}\limits_{\mathbf{Z}}p(\mathbf{X},\mathbf{Z}) \\
& = \mathop{\rm arg~max}\limits_{\mathbf{Z}}\ln p(\mathbf{X},\mathbf{Z}) \\
\end{aligned}$$
を解くことになります。
これを再帰的に計算するアルゴリズムをビタビアルゴリズム(Viterbi algorithm)と呼びます。</p>
まず、$\mathop{\rm max}\limits_{\mathbf{Z}}\ln p(\mathbf{X},\mathbf{Z})$ について考えます。
これに、先ほど導いた
$$p(\mathbf{X}, \mathbf{Z} | \boldsymbol{\theta})=p\left(\mathbf{z}_{1} | \boldsymbol{\pi}\right)\left[\prod_{n=2}^{N} p\left(\mathbf{z}_{n} | \mathbf{z}_{n-1}, \mathbf{A}\right)\right] \prod_{m=1}^{N} p\left(\mathbf{x}_{m} | \mathbf{z}_{m}, \boldsymbol{\phi}\right)\qquad (13.10)$$
を代入すると、以下の式を得ます。
$$\mathop{\rm max}\limits_{\mathbf{Z}}\ln p(\mathbf{X},\mathbf{Z}) = \mathop{\rm max}\limits_{\mathbf{Z}} \left\{ \ln p\left(\mathbf{z}_{1} | \boldsymbol{\pi}\right) + \sum_{n=2}^N \ln p\left(\mathbf{z}_{n} | \mathbf{z}_{n-1}, \mathbf{A}\right) + \sum_{n=1}^N \ln p\left(\mathbf{x}_{m} | \mathbf{z}_{m}, \boldsymbol{\phi}\right) \right\}$$
そこで、以下のように $\omega\left(\mathbf{z}_{n}\right)$ を定義します。
$$\omega\left(\mathbf{z}_{n}\right)=\max _{\mathbf{z}_{1}, \ldots, \mathbf{z}_{n-1}} p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{n}, \mathbf{z}_{1}, \ldots, \mathbf{z}_{n}\right)\qquad (13.70)$$
すると、$\mathop{\rm max}\limits_{\mathbf{Z}} \ln p(\mathbf{X},\mathbf{Z}) = \mathop{\rm max}\limits_{\mathbf{z}_N}\omega\left(\mathbf{z}_{n}\right)$ を得ます。
ここで、$\omega$ は次の漸化式を満たします。 $$\begin{aligned} \omega(\mathbf{z}_{n+1}) & = \mathop{\rm max}\limits_{\mathbf{z}_1,\ldots,\mathbf{z}_n}\left\{ \ln p(\mathbf{z}_1) + \sum_{i=2}^{n+1}\ln p(\mathbf{z}_i|\mathbf{z}_{i-1}) + \sum_{i=1}^{n+1} \ln p(\mathbf{x}_i|\mathbf{z}_i)\right\} \\ & = \mathop{\rm max}\limits_{\mathbf{z}_1,\ldots,\mathbf{z}_n}\left\{ \ln p(\mathbf{z}_1) + \sum_{i=2}^{n+1}\ln p(\mathbf{z}_i|\mathbf{z}_{i-1}) + \sum_{i=1}^{n+1} \ln p(\mathbf{x}_i|\mathbf{z}_i)\right\} \\ & \qquad + \ln p(\mathbf{z}_{n+1}|\mathbf{z}_n) + \ln p(\mathbf{x}_{n+1}|\mathbf{z}_{n+1})\\ & = \ln p(\mathbf{x}_{n+1}|\mathbf{z}_{n+1}) + \mathop{\rm max}\limits_{\mathbf{z}_n}\left\{\ln p(\mathbf{z}_{n+1}|\mathbf{z}_n) + \omega(\mathbf{z}_n)\right\} \end{aligned}$$</p>
これは、 $$\omega\left(\mathbf{z}_{1}\right)=\ln p\left(\mathbf{z}_{1}\right)+\ln p\left(\mathbf{x}_{1} | \mathbf{z}_{1}\right)\qquad (13.69)$$ によって初期化されます。
ここで、漸化式
$$\omega(\mathbf{z}_{n+1}) = \ln p(\mathbf{x}_{n+1}|\mathbf{z}_{n+1}) + \mathop{\rm max}\limits_{\mathbf{z}_n}\left\{\ln p(\mathbf{z}_{n+1}|\mathbf{z}_n) + \omega(\mathbf{z}_n)\right\}$$
において、$\mathbf{z}_{n+1}$ が決まると、$\max$ の部分の $\mathbf{z}_n$ の値が決まります。この関数関係 $\mathbf{z}_{n+1}\rightarrow\mathbf{z}_n$ を $\mathrm{pred}$ と書く事にします。つまり、
$$\mathrm{pred}(\mathbf{z}_{n+1}) = \mathop{\rm arg~max}\limits_{\mathbf{z}_n}\left\{\ln p(\mathbf{z}_{n+1}|\mathbf{z}_n) + \omega(\mathbf{z}_n)\right\}$$
となります。
これを用いることで、左から右に、「$\mathbf{z}_n = k$ の時に、そこより過去の部分の対数尤度が最大となるようなラベルの系列」が計算されていきます。
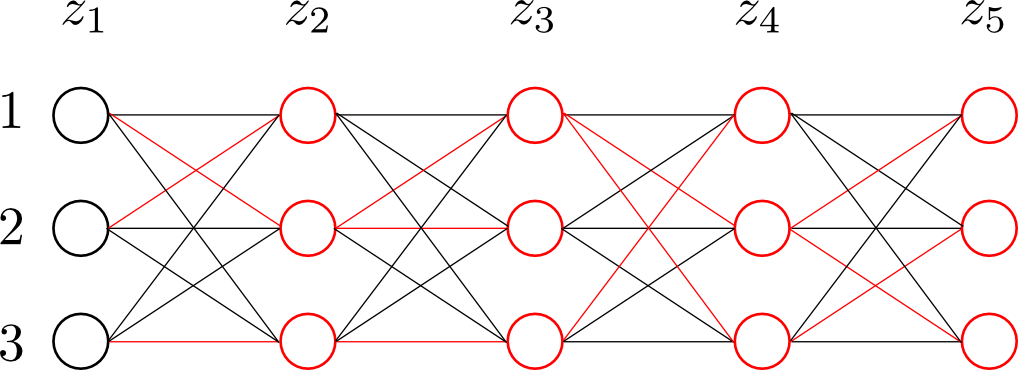
求める隠れ変数の系列は
$$\begin{aligned}
\hat{\mathbf{Z}}
& = \mathop{\rm arg~max}\limits_{\mathbf{Z}}\log p(\mathbf{X},\mathbf{Z}) \\
& = \mathop{\rm arg~max}\limits_{\mathbf{z}_N}\omega(\mathbf{z}_N)
\end{aligned}$$
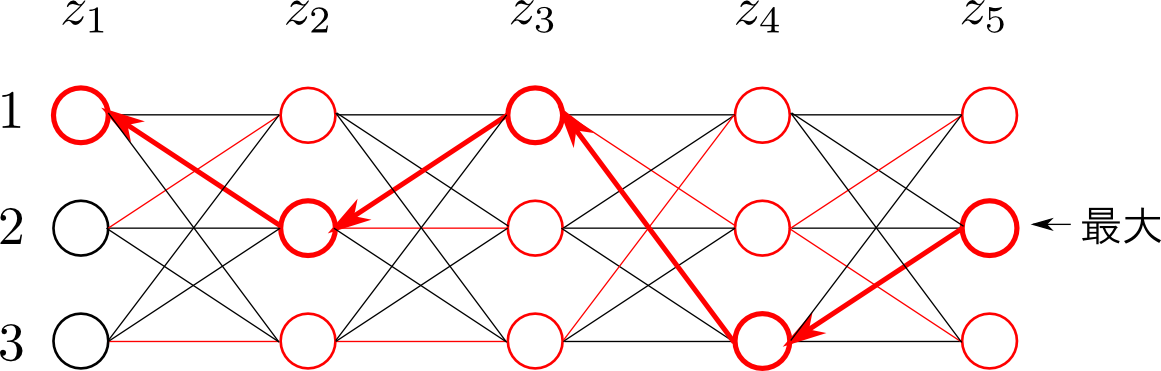
だったので、まず $\mathbf{z}_N$ を決めます。すると、$\mathrm{pred}$ によって $\mathbf{z}_{N-1} = \mathrm{pred}(\mathbf{z}_N)$ が決まります。
これを繰り返すことで、系列 $\mathbf{z}_1 \rightarrow \mathbf{z}_2 \rightarrow \cdots \mathbf{z}_{N-1} \rightarrow \mathbf{z}_N$ が右から順番に求まることになります。いわゆるバックトラッキング(backtracking)という計算です。</p>
Program¶
実際に使用してみる。以下のプログラムは、fit, E_step, M_step が本質的な情報で残りは綺麗に結果を出力するだけの関数です。
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
base2int = dict([("A",0),("T",1),("G",2),("C",3)]) # 辞書（indexで管理）
int2base = dict([(0,"A"),(1,"T"),(2,"G"),(3,"C")]) # 逆の辞書
class HMM():
def __init__(self, M, K, sequences):
self.M = M # x（データ）の種類
self.K = K # z（状態）の種類
self.sequences =[base2int[base] for base in Bases] # 塩基配列を数字で表す。
#=== モデルのパラメータ初期化 ===
# 初期状態
self.pi = np.random.uniform(0.25,0.75, K) # πの初期化。極端な値をとると最適化できない。
self.pi = self.pi / np.c_[self.pi.sum()]
# 遷移確率
self.A = np.eye(K) + np.random.uniform(0,0.2, [K,K]) # Aの初期化(対角成分の確率を高める)
self.A /= np.c_[self.A.sum(1)]
# 放出確率
self.phi = np.random.uniform(0.25, 0.75, (M, K)) # φの初期化
self.phi /= self.phi.sum(0)
def fit(self, ITER_MAX=1000):
for it in range(ITER_MAX):
# 更新前のパラメタを記録
past_params = np.hstack((self.pi.ravel(),
self.A.ravel(),
self.phi.ravel()))
#=== E step ===
gamma, xi = self.E_step()
#=== M step ===
self.M_step(gamma,xi)
#=== 終了条件(更新後のパラメータが近似的に等しいかを調べる) ===
params = np.hstack((self.pi.ravel(),
self.A.ravel(),
self.phi.ravel()))
if np.allclose(params, past_params, rtol=1e-05, atol=1e-08):
break
return it
def E_step(self):
N = len(self.sequences)
#=== 前向き後向きアルゴリズムの漸化式 ===
alpha = np.zeros([N,self.K]) # 前向きアルゴリズムのαを記録
beta = np.zeros([N,self.K]) # 後向きアルゴリズムのβを記録
alpha[0] = self.pi * self.phi[self.sequences[0]] # 初期化：α(z1) = p(x1|φ_z1)π_z1
beta[-1] = 1 # 初期化：β(zN) = 1
#=== 動的計画法でαを計算 ===
for i in range(1, len(self.sequences)):
# α(zi) = ∑z_i−1 α(z_i−1) A_zi−1,zi * p(xi|ϕ_zi)
alpha[i] = self.A.dot(alpha[i-1]) * self.phi[self.sequences[i]]
#=== 動的計画法でβを計算 ===
for i in reversed(range(len(self.sequences)-1)):
# β(zi) = ∑β(z_i+1) p(x_i+1|ϕz_i+1) A_zi,zi+1
beta[i] = (beta[i+1] * self.phi[self.sequences[i+1]]).dot(self.A)
#=== 上のα,βから、γを計算 α(zi)β(zi)/p(x) ===
gamma = alpha * beta
gamma /= np.sum(gamma, axis=1, keepdims=True)
#=== 上のα,βから、ξを計算 ξ_i = α(z_i-1)β(zi)p(zi|φ_zi)A_z_i-1,zi / p(x) ===
xi = self.A * (self.phi[self.sequences[1:]] * beta[1:])[::,None] * alpha[:-1, None, :]
xi /= np.sum(xi, axis=(1,2), keepdims=True)
return gamma, xi
def M_step(self,gamma,xi):
#=== 初期状態のパラメタπを更新 πk=γ_1k/∑γ_1k ===
self.pi = gamma[0] / np.sum(gamma[0])
#=== 遷移確率のパラメタAの更新 Ajk=∑ξ_ijk/∑∑ξijk ===
self.A = np.sum(xi, axis=0) / np.sum(xi, axis=(0,2))
self.A /= np.sum(self.A, axis=0, keepdims=True)
#=== 放出確率のパラメタφの更新 ϕ_kj=∑γ_ik*x_ij/∑∑γ_ik * x_ij ===
x = gamma[:, None, :] * (np.eye(self.M)[self.sequences])[:,:,None]
self.phi = np.sum(x, axis=0) / np.sum(gamma, axis=0)
def plot(self):
it = model.fit()
gamma, _ = model.E_step()
plt.plot(np.argmax(gamma, axis=1))
plt.title("state translation. (iteration={})".format(it+1))
plt.show()
def plot_initial_state(self):
for k in range(self.K):
print("z({}): {:.3f}".format(k+1,self.pi[k]))
def plot_translation(self):
model.fit()
print(" 【Before state】")
z_format = " "
for k in range(self.K):
z_format += "z({}) ".format(k+1)
print(z_format)
for j in range(self.K):
print(" z({}) ".format(k+1), end="")
A_form = ""
for k in range(self.K):
A_form += "{:.3f} ".format(self.A[j][k])
print(A_form)
def plot_emission(self):
model.fit()
z_format = " \ "
for k in range(self.K):
z_format += "z({}) ".format(k+1)
print(z_format)
for j in range(self.M):
print(" {} ".format(int2base[j]), end="")
phi_form = ""
for k in range(self.K):
phi_form += "{:.3f} ".format(self.phi[j][k])
print(phi_form)
def plot_state_translation(self):
model.fit()
gamma, _ = model.E_step()
for k in range(self.K):
plt.plot(gamma[:,k], alpha=0.7, label="z({})".format(k+1))
plt.legend()
plt.show()
def plot_state(self):
model.fit()
gamma, _ = model.E_step()
return np.argmax(gamma, axis=1)
#=== 学習データを作成（非常に極端な例です） ===
Bases = []
for i in range(100):
if i< 20:
Bases.append(np.random.choice(["T","C"])) # ピリミジン塩基のみ
elif i>= 80:
Bases.append(np.random.choice(["A","G"])) # プリン塩基のみ
else:
Bases.append(np.random.choice(["A","T","G","C"])) # 一般的
np.array(Bases)
model = HMM(4,3,Bases)
model.plot()
model.plot_state_translation()
model.plot_state()
model.plot_emission()
sns.heatmap(model.phi, vmax=1, vmin=0, cmap='coolwarm')
plt.show()
model.plot_initial_state()
model.plot_translation()
sns.heatmap(model.A, vmax=1, vmin=0, cmap='coolwarm')
plt.show()
発展¶
実際の塩基配列を公共データベースであるDDBJ 日本DNAデータバンク から入手し、適当な状態数でモデル化をすると、今まで気づかなかった発見などがあるかもしれません。「機械学習」などの、「機械に特徴を学習させる学問」は、そこが面白さの１つだと考えています。
アプローチの仕方は全く異なりますが、「今まで人間が発見できなかった事実に気づける」という面では、順遺伝学にも似ていると感じています。それが僕が生物情報科学かを選んだ理由でもあります。