- 講師:津田宏治
- 資料:生物データマイニング論(2019)
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
- データ駆動科学とベイズ最適化
- データ駆動科学では、データに基づいて、新たな知見・事柄を発見することが求められる
- 単に予測を行うだけでなく、それに基づいて「行動」を設計することが必要
- これらは、「ベイズ最適化」の枠組みに乗ることが多い
ベイズ線形回帰
- 線形回帰モデルのパラメータを最尤推定によって決める場合、解こうとしている問題に合わせてモデルの複雑さを適切に決めることが必要
- ↑は、単純に尤度を最大化するだけでは過学習を引き起こしてしまう。
- データの一部を独立なテスト用データとして取っておくことでモデルの汎化性能を評価できるが、この方法は計算量が大きく、データの無駄遣いとなり得る。
これらの問題に対処するため、線形回帰モデルをベイズ的に取り扱うことで最尤推定の過学習を回避するとともに「訓練データだけからモデルの複雑さを自動的に決定する。」
概要¶
- 解こうとしている問題に沿った尤度関数(likelihood function)( $p(\mathbf{t}|\mathbf{X},\mathbf{w})$ )を定義する。
- モデルパラメータの事前分布(prior distribution)( $p(\mathbf{w})$ )を、尤度関数の共役事前分布(conjugate prior)の形で定義する。
- ベイズの公式より、事後分布(posterior distribution)は事前分布と尤度関数の積に比例する。( $p(\mathbf{w}|\mathbf{t},\mathbf{X})\propto p(\mathbf{t}|\mathbf{X},\mathbf{w})\cdot p(\mathbf{w})$ )
- あるパラメータ( $\mathbf{w}$ )下で入力 $\mathbf{x}$ が与えられた時の確率分布( $p(t|\mathbf{w},\mathbf{x})$ )を、3で求めた事後分布( $p(\mathbf{w}|\mathbf{t},\mathbf{X})$ )で重み付けしながら周辺化(marginalization)する( $p(t|\mathbf{t},\mathbf{X},\mathbf{x}) = \int p(t|\mathbf{w},\mathbf{x})p(\mathbf{w}|\mathbf{t},\mathbf{X})d\mathbf{w}$ )ことで、予測分布(predivtive distribution)( $p(t|\mathbf{w},\mathbf{x})$ )を得る。
具体例¶
※ $D$ 次元の説明変数 $\mathbf{x}$ で一次元の目標変数 $t$ を線形回帰するモデルをベイズ的に取り扱う。
- 目標変数 $t$ が決定論的な関数 $y(\mathbf{x},\mathbf{w})$ と加法性のガウスノイズの和で与えられる場合を考える。 $$t = y(\mathbf{x},\mathbf{w}) + \epsilon\qquad (3.7)$$ ここで、$\epsilon$ は期待値が $0$ で精度が $\beta$ のガウス確率変数である。すなわち、以下で表すことができる。 $$p(t|\mathbf{x},\mathbf{w},\beta) = \mathcal{N}\left(t|y(\mathbf{x},\mathbf{w}),\beta^{-1}\right)\qquad (3.8)$$
- データ点が $(3.8)$ の分布から独立に生成されたと仮定すると、尤度関数を次のように表せる。 $$p(\mathbf{t}|\mathbf{X},\mathbf{w},\beta) = \prod_{n=1}^N\mathcal{N}\left(t_n|\mathbf{w}^T\phi(\mathbf{x}_n),\beta^{-1}\right)\qquad (3.10)$$
- モデルパラメータ $\mathbf{w}$ の事前分布を導入する。ここで、$\beta$ が既知と仮定すると、上記の尤度関数の共役事前分布である、期待値 $\mathbf{m}_0$ 共分散 $\mathbf{S}_0$ を持つガウス分布で表すのが適当である。 $$p(\mathbf{w}) = \mathcal{N}(\mathbf{w}|\mathbf{m}_0,\mathbf{S}_0)\qquad (3.48)$$ ※ なお、$\mathbf{w},\beta$ の両方が未知である場合、共役事前分布はガウス-ガンマ分布隣、予測分布はスチューデントのt分布となる。
- ベイズの公式より、事後分布は事前分布と尤度関数の積に比例するので、これを解くことで事後分布を次の形で書き出すことができる。(導出) $$ p(\mathbf{w}|\mathbf{t},\mathbf{X},\beta) = \mathcal{N}(\mathbf{w}|\mathbf{m}_N,\mathbf{S}_N) \qquad (3.49)\\ \begin{cases} \mathbf{m}_N &= \mathbf{S}_N\left(\mathbf{S}_0^{-1}\mathbf{m}_0 + \beta\boldsymbol{\Phi}^T\mathbf{t}\right) & (3.50)\\ \mathbf{S}_N^{-1} &= \mathbf{S}_0^{-1} + \beta\boldsymbol{\Phi}^T\boldsymbol{\Phi} & (3.51) \end{cases} $$
- $\mathbf{w}$ で周辺化することで、予測分布を求めるが、議論の簡単のために、「モデルパラメータ $\mathbf{w}$ の事前分布 $p(\mathbf{w})$ が、単一の制度パラメータ $\alpha$ で記述される期待値が $0$ の等方的ガウス分布である」とする。 $$p(\mathbf{w}|\alpha) = \mathcal{N}\left(\mathbf{w}|\mathbf{0},\alpha^{-1}\mathbf{I}\right)\qquad (3.52)$$ この時、上記の $\mathbf{w}$ の事後分布 $(3.49)$ の形は変わらず、$\mathbf{m}_N,\mathbf{S}_N$ の値が $$ \begin{cases} \mathbf{m}_N &= \beta\mathbf{S}_N\boldsymbol{\Phi}^T\mathbf{t} & (3.53)\\ \mathbf{S}_N^{-1} &= \alpha\mathbf{I} + \beta\boldsymbol{\Phi}^T\boldsymbol{\Phi} & (3.54) \end{cases} $$ となる。この条件下で周辺化すると、以下の結果を得る。(導出) $$ \begin{aligned} p(t|\mathbf{t},\mathbf{X},\mathbf{x},\alpha,\beta) &= \int p(t|\mathbf{w},\mathbf{x},\beta)p(\mathbf{w}|\mathbf{t},\mathbf{X},\alpha,\beta)d\mathbf{w}& (3.57)\\ &= \mathcal{N}\left(t|\mathbf{m}_N^T\phi(\mathbf{x}),\sigma_N^2(\mathbf{x})\right) & (3.58)\\ \sigma_N^2(\mathbf{x}) &= \frac{1}{\beta} + \phi(\mathbf{x})^T\mathbf{S}\phi(\mathbf{x}) & (3.59) \end{aligned} $$ ※ ここで、$(3.59)$ の第1項はデータに含まれるノイズを、第2項は $\mathbf{w}$ に関する不確かさを反映している。
事後分布の計算の導出過程
周辺化計算の導出過程
以下の「ガウス分布の周辺分布と条件付き分布の関係」の $(2.115)$ の結果を用いる。
$\mathbf{x}$ の周辺ガウス分布と、$\mathbf{x}$ が与えられた時の $\mathbf{y}$ の条件付きガウス分布が次式で与えられたとする。
$$ \begin{aligned} p(\mathbf{x}) &=\mathcal{N}\left(\mathbf{x} | \boldsymbol{\mu}, \mathbf{\Lambda}^{-1}\right) & (2.113)\\ p(\mathbf{y} | \mathbf{x}) &=\mathcal{N}\left(\mathbf{y} | \mathbf{A} \mathbf{x}+\mathbf{b}, \mathbf{L}^{-1}\right) & (2.114)\end{aligned} $$この時、$\mathbf{y}$ の周辺分布と、$\mathbf{y}$ が与えられた時の $\mathbf{x}$ の条件付き分布は
$$ \begin{aligned} p(\mathbf{y}) &=\mathcal{N}\left(\mathbf{y} | \mathbf{A} \boldsymbol{\mu}+\mathbf{b}, \mathbf{L}^{-1}+\mathbf{A} \mathbf{\Lambda}^{-1} \mathbf{A}^{\mathrm{T}}\right) & (2.115)\\ p(\mathbf{x} | \mathbf{y}) &=\mathcal{N}\left(\mathbf{x} | \mathbf{\Sigma}\left\{\mathbf{A}^{\mathrm{T}} \mathbf{L}(\mathbf{y}-\mathbf{b})+\mathbf{\Lambda} \boldsymbol{\mu}\right\}, \mathbf{\Sigma}\right) & (2.116) \end{aligned} $$で与えられる。ただし、
$$\mathbf{\Sigma} = \left(\mathbf{\Lambda} + \mathbf{A}^T\mathbf{LA}\right)^{-1}\qquad (2.117)$$である。
実装¶
from kerasy.ML.linear import BayesianLinearRegression
from kerasy.utils.preprocessing import GaussianBaseTransformer
from kerasy.utils.data_generator import generateSin, generateGausian
N = 25; D = 1; M = 25
xmin=0; xmax=1
seed = 10
alpha = 1
beta = 25
x_test = np.linspace(xmin,xmax,1000)
y_test = np.sin(2*np.pi*x_test)
x_train,y_train = generateSin(size=N, xmin=xmin,xmax=xmax,seed=seed)
_,y_noise = generateGausian(size=N, x=x_train, loc=0, scale=1/beta, seed=seed)
y_train += y_noise
# transform
mu = np.linspace(xmin,xmax,M); sigma = 0.1
phi = GaussianBaseTransformer(mu=mu, sigma=sigma)
x_train_features = phi.transform(x_train)
x_test_features = phi.transform(x_test)
random_idx = np.random.RandomState(seed).choice(N, N)
fig = plt.figure(figsize=(16,8))
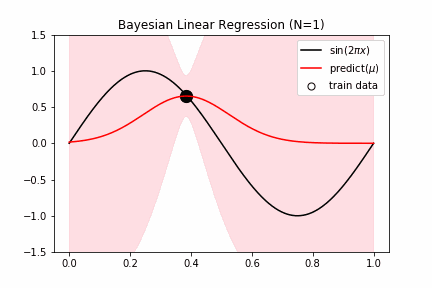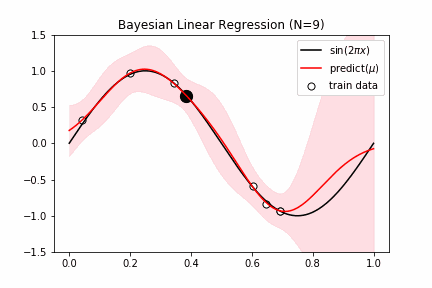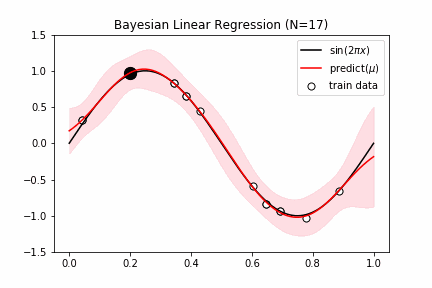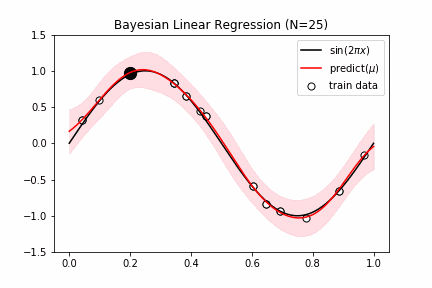
for i,n in enumerate([1,2,4,25]):
ax = fig.add_subplot(2,2,i+1)
model = BayesianLinearRegression(alpha=alpha, beta=beta)
model.fit(x_train_features[random_idx[:n]],y_train[random_idx[:n]])
y_pred,y_std = model.predict(x_test_features)
ax.plot(x_test,y_test,color="black", label="$\sin(2\pi x)$")
ax.plot(x_test,y_pred,color="red", label="predict($\mu$)")
ax.fill_between(x_test, y_pred-y_std, y_pred+y_std, color="pink", alpha=0.5)
ax.scatter(x_train[random_idx[:n]],y_train[random_idx[:n]],s=150,edgecolors='black',facecolor="white",label="train data")
ax.set_ylim(-1.5,1.5), ax.legend(), ax.set_title(f"Bayesian Linear Regression (N={n})")
plt.tight_layout()
plt.show()
ガウシアンプロセス
- 回帰分析のためのカーネル法
- テストサンプルに対して、予測値だけでなく、予測分散も与えることができる。
線形回帰のモデルは、以下で表されていた。
$$y(\mathbf{x},\mathbf{w}) = \mathbf{w}^T\phi(\mathbf{x})\qquad (3.3)$$この結果に、ベイズ線形回帰の結果 $(3.53)$ を代入すると、
$$ \begin{aligned} y(\mathbf{x},\mathbf{m}_N) &= \mathbf{m}_N\phi(\mathbf{x}) = \beta\phi(\mathbf{x})^T\mathbf{S}_N\boldsymbol{\Phi}^T\mathbf{t} \\ &= \sum_{n=1}^N\beta\phi(\mathbf{x})^T\mathbf{S}_N\phi(\mathbf{x}_n)t_n & (3.60)\\ \mathbf{S}_N^{-1} &= \mathbf{S}_0^{-1} + \beta\boldsymbol{\Phi}^T\boldsymbol{\Phi} & (3.51) \end{aligned} $$したがって、点 $\mathbf{x}$ での予測分布の平均は訓練データの目標変数 $t_n$ の線型結合で与えられるので、
$$ \begin{aligned} y(\mathbf{x},\mathbf{m}_N) &= \sum_{n=1}^Nk(\mathbf{x}, \mathbf{x}_n)t_n & (3.61)\\ k(\mathbf{x}, \mathbf{x}^{\prime}) &= \beta\phi(\mathbf{x})^T\mathbf{S}_N\phi(\mathbf{x}^{\prime}) & (3.62)\\ &= \left(\beta^{1/2}\mathbf{S}_N^{1/2}\phi(\mathbf{x})\right)^T\left(\beta^{1/2}\mathbf{S}_N^{1/2}\phi(\mathbf{x})\right) & (3.65) \end{aligned} $$とかける。なお、$k(\mathbf{x}, \mathbf{x}^{\prime})$ を平滑化行列(smoother matrix)、または等価カーネル(equivalent kernel)と呼ぶ。($(3.65)$ から、等価カーネルが通常のカーネル関数が満たすべき性質を満たしていることがわかる。)
また、訓練データの目標値の線型結合を取ることで予測を行う上記のような回帰関数を線形平滑器(linear smoother)と呼ぶ。
from kerasy.utils.preprocessing import GaussianBaseTransformer, SigmoidBaseTransformer, PolynomialBaseTransformer
X = np.linspace(-1,1,200)
M = 15
mu = np.linspace(-0.9,0.9,M);
sigma = 0.1
gausian_phi = GaussianBaseTransformer(mu=mu, sigma=sigma)
def mkSmootherMatrix(X, phi, alpha=1, beta=25):
X_feature = phi.transform(X)
N,M = X_feature.shape
SN = np.linalg.inv(alpha*np.eye(M) + beta*X_feature.T.dot(X_feature))
K = beta*np.dot(X_feature, np.dot(SN, X_feature.T))
return K
K = mkSmootherMatrix(X, gausian_phi)
SP = [30, 120, 150]
colors = ["red","salmon","pink"]
fig = plt.figure(figsize=(12,6))
axKernel = plt.subplot2grid((3, 2), (0, 1), rowspan=3)
axKernel = sns.heatmap(K, vmin=np.min(K), vmax=np.max(K), cmap="jet", cbar=False, square=True, ax=axKernel)
axKernel.set_xticks([]), axKernel.set_yticks([])
axKernel.set_xlabel("$x$", fontsize=18), axKernel.set_ylabel("$x^{\prime}$", fontsize=18)
for i in range(3):
axL = plt.subplot2grid((3, 2), (i, 0))
axL.set_facecolor('lightcyan')
axL.plot(K[SP[i]], color=colors[i], linewidth=4)
axL.set_xticks([]), axL.set_yticks([])
axKernel.axhline(SP[i], color=colors[i], linewidth=10, alpha=0.7)
plt.tight_layout()
plt.show()
Transformers = [
(GaussianBaseTransformer, mu),
(SigmoidBaseTransformer, mu),
(PolynomialBaseTransformer, 10),
]
fig = plt.figure(figsize=(12,4))
for i,(phi_func, param) in enumerate(Transformers):
ax = fig.add_subplot(1,3,i+1)
phi = phi_func(param)
K = mkSmootherMatrix(X, phi)
ax.plot(K[100], color="blue")
ax.scatter(100,0,color="red", marker="x", s=150, label="$x^{\prime}$")
ax.set_xticks([]), ax.set_yticks([]), ax.set_title(f"$k(x,x')$: {phi.__name__}", fontsize=16)
ax.set_xlabel("$x$", fontsize=18), ax.legend()
plt.tight_layout()
plt.show()
カーネル関数の例を見ればわかるよう、対応する基底関数が局所的でないにも関わらず、等価カーネルは $x^{\prime}$ に関して局所的な関数となっていることがわかる!!
また、$y(\mathbf{x})$ と $y(\mathbf{x}^{\prime})$ の共分散を考えると、
$$ \begin{aligned} \mathrm{cov}\left[y(\mathbf{x}),y(\mathbf{x}^{\prime})\right] &= \mathrm{cov}\left[\phi(\mathbf{x})^T\mathbf{w}, \mathbf{w}^T\phi(\mathbf{x})\right]\\ &= \phi(\mathbf{x})^T\mathbf{S}_N\phi(\mathbf{x}^{\prime}) = \beta^{-1}k(\mathbf{x},\mathbf{x}^{\prime})\quad(3.63) \end{aligned} $$となる。ここで、上述の等価カーネルの形状を考えると、近接での予測平均は互いに強い相関を持っている一方で、より離れた点の組では相関は小さくなることがわかる。
ベイズ線形回帰のように基底関数の集合を明示的に定義するのではなく、局所的なカーネルを直接定義し、観測された訓練集合が与えられた時、この局所的なカーネルを用いて新たな入力ベクトル $\mathbf{x}$ に対する予測値を求めることができる。
この定式化から、回帰(と分類)に対する実用的な枠組みであるガウス過程(Gaussian process)が得られる。
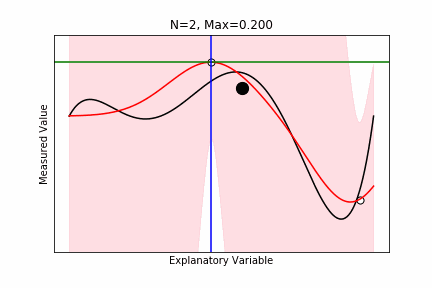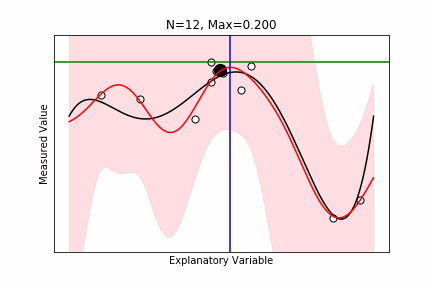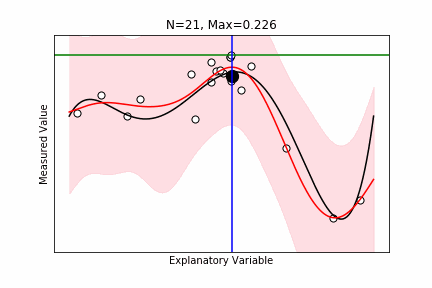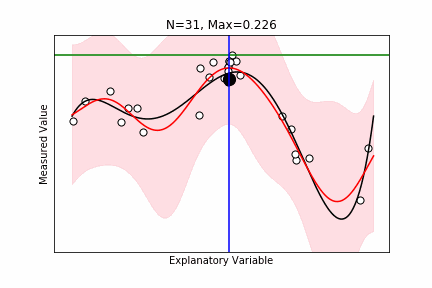
ベイズ最適化
- $M$ 個の候補点があり、この中から最大の観測値を持つものを探したい。
- できるだけ実験数を少なくしたい。
- $N$ 個の候補点に対する実験が終わった。$M-N$ 個の候補点が残っている。
- 次の $N+1$ 個目の候補点を最適に選びたい。
- $N$ 個の化合物から予測モデルを学習し、それを用いて、残りの候補点をスコアリングし決定。
- Maximum Probability of Improvement: Current Maxを超える確率。
- Maximum Expected Improvement: (観測値-Current Max)の期待値。
- Thompson Sampling: 残りのM-N個候補点に対して、条件つき結合確率からサンプリングを行い、そのサンプリング値をスコアとする。
xmin = 0; xmax = 1
N=1000; M=25
seed = 1
alpha = 1
beta = 25
X = np.linspace(xmin,xmax,N)
Y = 5e1*X*(X-0.2)*(X-0.3)*(X-0.7)*(X-1)
_,noise = generateGausian(size=1000, x=X, loc=0, scale=1/beta, seed=seed)
Y_ob = Y+noise
mu = np.linspace(xmin,xmax,M)
sigma = 0.1
phi = GaussianBaseTransformer(mu=mu, sigma=sigma)
X_features = phi.transform(X)
fig = plt.figure(figsize=(18,8))
idx = np.random.RandomState(seed).choice(N, 2) # Initialization.
next_idx = idx
for i,_ in enumerate(range(12)):
ax = fig.add_subplot(3,4,i+1)
model = BayesianLinearRegression(alpha=alpha, beta=beta)
model.fit(X_features[idx], Y_ob[idx])
y_pred,y_std = model.predict(X_features)
current_max = np.max(Y_ob[idx])
max_improve_id = np.argmax(y_pred)
ax.plot(X, Y, color="black", label="True distribution")
ax.plot(X, y_pred,color="red", label="predict($\mu$)")
ax.fill_between(X, y_pred-y_std, y_pred+y_std, color="pink", alpha=0.5)
ax.scatter(X[idx],Y_ob[idx],s=50,edgecolors='black',facecolor="white",label="Observation")
ax.scatter(X[next_idx],Y_ob[next_idx],s=150,edgecolors='black',facecolor="black",label="New Obsevation")
ax.set_xlabel("Explanatory Variable"), ax.set_ylabel("Measured Value"), ax.set_title(f"N={len(idx)}, Max={current_max:.3f}")
ax.set_ylim(-0.5,0.3), ax.set_xticks([]), ax.set_yticks([])
ax.axhline(current_max, color="green", label="Current Maximum")
ax.axvline(np.max(X[max_improve_id]), color="blue", label="Maximum Probability of Improvement")
next_idx = max_improve_id if np.random.uniform()>0.5 else np.random.choice(N, 1)
idx = np.r_[idx, next_idx]
ax.legend()
plt.tight_layout()
plt.show()
おわりに(データ駆動科学)
- データ駆動科学では、データに基づいて、新たな知見・事柄を発見することが求められる。
- 単に予測を行うだけでなく、それに基づいて次の「行動」を設計することが必要
- これらは、ベイズ最適化の枠組みに乗ることが多い。