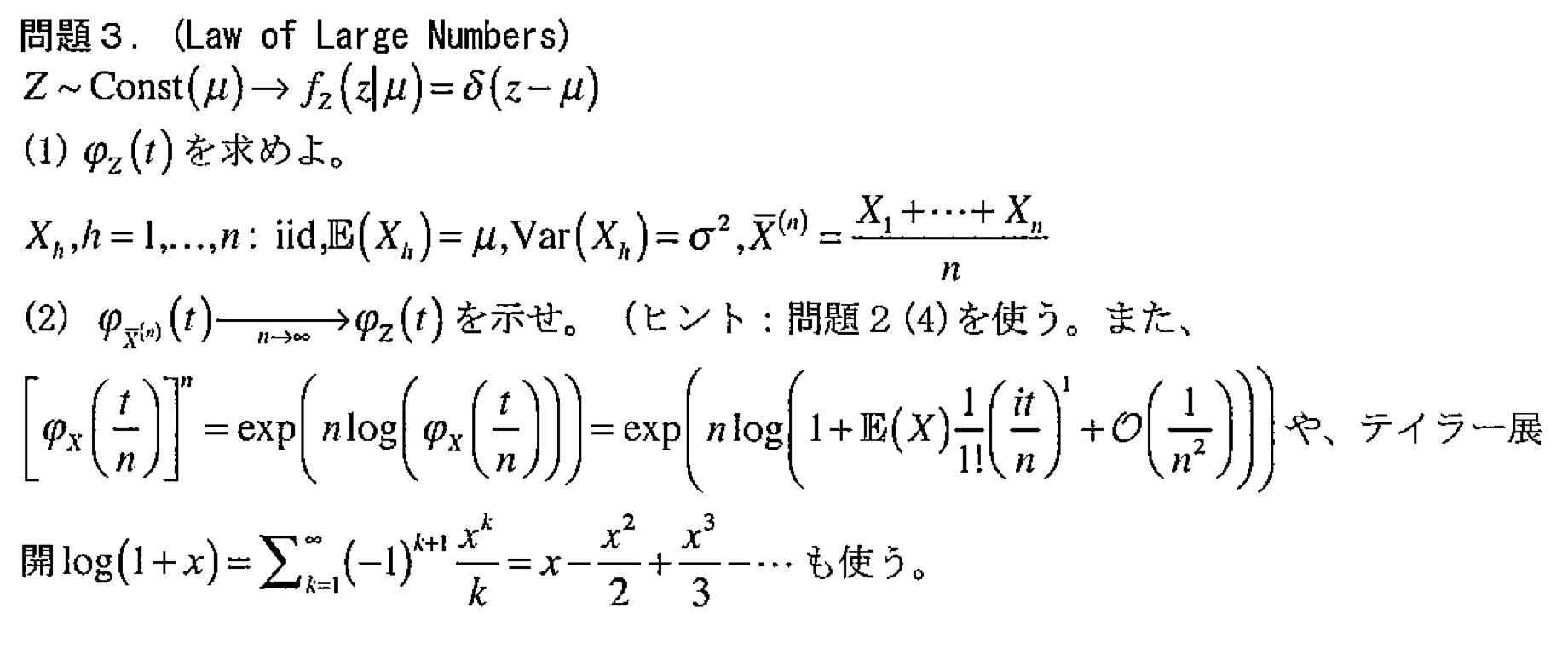
解答
1
$$
\begin{aligned}
\varphi_{Z}(t) &= \int_{-\infty}^{\infty}e^{itz}\delta\left(z-\mu\right)dz\\
&= e^{it\mu}
\end{aligned}
$$
2
$$
\begin{aligned}
\varphi_{\bar{X}^{(n)}}(t)
&= \varphi_{\frac{X_1 + \cdots + X_n}{n}}(t)\\
&= \varphi_X\left(\frac{X_1}{n}\right)\cdots\varphi_X\left(\frac{X_n}{n}\right)\\
&= \left[\varphi_X\left(\frac{X}{n}\right)\right]^n\\
&= \exp\left(n\log\left(\varphi_X\left(\frac{X}{n}\right)\right)\right)\\
&= \exp\left(n\log\left(1 + \mathbb{E}\left(X\right)\frac{1}{1!}\left(\frac{it}{n}\right)^1 + \mathcal{O}\left(\frac{1}{n^2}\right)\right)\right)\\
\end{aligned}
$$
ここで、
$$
\begin{aligned}
&\log\left(1 + \mathbb{E}\left(X\right)\frac{1}{1!}\left(\frac{it}{n}\right)^1 + \mathcal{O}\left(\frac{1}{n^2}\right)\right)\\
&= \sum_{k=1}^{\infty}\left(-1\right)^{k+1}\cdot\frac{\left(\mathbb{E}\left(X\right)\frac{it}{n} + \mathcal{O}\left(\frac{1}{n^2}\right)\right)^k}{k}\\
&= \mathbb{E}\left(X\right)\frac{it}{n} + \mathcal{O}\left(\frac{1}{n^2}\right)
\end{aligned}
$$
だから、
$$
\begin{aligned}
\varphi_{\bar{X}^{(n)}}(t)
&= \exp\left(n\cdot\mathbb{E}\left(X\right)\frac{it}{n} + \mathcal{O}\left(\frac{1}{n}\right)\right)\\
&= \exp\left(it\mu + \mathcal{O}\left(\frac{1}{n}\right)\right)\\
&\underset{n\rightarrow\infty}{\longrightarrow}e^{it\mu} = \varphi_{\bar{X}^{(n)}}(t)
\end{aligned}
$$