4.Guided NEST exercises (intermediate)

Unit	Neural Coding and Brain Computing Unit (Tomoki Fukai)
Teacher	Thomas Burns
Lecture Material	https://github.com/oist-ncbc/skill-pill-plus/tree/master/Tutorial-4_Plasticity-and-Learning
Library	https://github.com/iwasakishuto/University/tree/gh-pages/3A/theme/program/OIST/tutorial4.py

Part 1: STDP and its varities¶

STDP alters the weights of synapses depending on the relative spike timing between the postsynaptic neuron and the presynaptic neuron.

_STDP overview (from Sjöström J, Gerstner W (2010) Spike-timing dependent plasticity. Scholarpedia)_

• Within some time windows:
  • if "PRE before POST", we get Long-Term Potentiation (LTP)
  • if "POST before PRE", we get Long-Term Depression (LTD)
• The time windows for LTP and LTD are generally on the order of tens of milliseconds.
• The LTD window is generally longer than the LTP window.

Implementation¶

• To implement STDP in spiking neural network models, different STDP rules can be used.
• In general, different rules result in different distributions of synaptic weights over the course of learning.
• Examples of such weight distributions are shown below.

STDP rules (from Gilson M, Fukai T (2011) Stability versus Neuronal Specialization for STDP. PLoS ONE)

• Additive STDP tends to produce competition between synapses but needs to have its weights bound to ensure network stability (e.g. to avoid over-excitation)
• Multiplicative STDP tends to produce less competition between synapses but owing to its weight-dependent manipulation of synaptic weights does not require artificial bounds.
• Logorithmic STDP attempts to reconcile the two.

Additive STDP rule¶

In the following exercise, we will use the additive STDP rule, sometimes also called the exponential STDP rule:

$$ \Delta w_j= \begin{cases} a^+ \cdot e^{\big( \dfrac{t_j-t_i}{\tau^+} \big)} & \text{if}\ t_j \leq t_i & \text{(LTP)} \\ -a^- \cdot e^{\big( - \dfrac{t_j-t_i}{\tau^-} \big)} & \text{if}\ t_j > t_i & \text{(LTD)} \end{cases} $$

variable	Meaning
$a^+$	learning rate for LTP
$a^-$	learning rate for LTD
$t_j$	spike time of the presynaptic neuron $j$
$t_i$	spike time of the postsynaptic neuron $i$
$\tau^+$	time constant for LTP (ms)
$\tau^-$	time constant for LTD (ms)

Using pre-defined paramaters which we will use in the second part of this tutorial, let's plot **"how the this STDP rule changes weights depending on the timing of presynaptic and postsynaptic spikes."**

• The closer the spike timing between the postsynaptic neuron and the presynaptic neuron are, the bigger the influence is.
• If a becomes larger, the STDP curve expand in the y-axis direction, and if tau becomes larger, the STDP curve shrink in the x-axis direction.
• When the time difference gets ver close to 0, weight changes will diverge and lead to over-excitation or network instability.

Part 2: Unsupervised pattern-detection using STDP¶

In this part of the tutorial we will be replicating the results from [Masquelier et al. (2008) Spike Timing Dependent Plasticity Finds the Start of Repeating Patterns in Continuous Spike Trains. PLoS ONE](https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0001377). (In fact, we already reproduced Figure 2 from their paper in the first part of this tutorial.)

• Masquelier et al. (2008) create a spiking neural network with
  • 2,000 presynaptic neurons
  • just one postsynpatic neuron.
• They implement additative STDP in this network, which allows the "postsynaptic neuron" to learn to detect the beginning of repeating patterns of spiking activity arriving from the 2,000 presynaptic neurons.
• Importantly, the presynaptic neurons also have periods of random, non-patterned activity and have additional noisy spiking activity at all times.

Let's begin by constructing the spike trains of the 2,000 presynaptic neurons.

We will run our simulations for 450s, so we will create 450s worth of spike trains for these neurons.

The first step is construct random activity with the following properties:

• Each presynpatic neuron will emit spikes independently
  • generated by a Poisson process with a variable instantaneous firing rate $r$
  • $r$ varies randomly beteen $0$ and $90$ Hz.
• The rate of change in $r$ is modified by $dr$
  • $dr$ starts at $0$
  • $dr$ is modified by $ds$, randomly picked from a uniform distribution over $[−360,+360]$ Hz/s.
  • $dr$ is clipped to within $[-1800,1800]$ Hz/s
• we will also manually add some additional spikes to guarantee that "in every 50ms time bin, each neuron spikes at least once"

Make a training data¶

Now we will

1. Divide the presynaptic spiking activity into segments of 50ms
2. Select a random 50ms segment to be considered as the "pattern"
3. Copy and paste this pattern across the raster plot in a certain proportion of segments.
4. Add 10Hz Noises to all neurons at all times.

Divide and Select "Pattern"¶

Copy and Paste this "Pattern"¶

Add Poisson Noises¶

Firing Rates¶

Check the Repeated Position¶

• With these paramaters, we can embed a repeating pattern within some pseduo-random, spontaneous activity.
• However, learning takes time! And we have only been simulating 1s of activity.
• In this task, the authors reported they needed 13.5s of activity (or 700 pattern presentations) for the neuron to show signs of learning to recognise the pattern.

Figure 4 from Masquelier et al. 2008: Overview of the 450 s simulation. Here we plotted the membrane potential as a function of simulation time, at the beginning, middle, and end of the simulation. Grey rectangles indicate pattern presentations. (a) At the beginning of the simulation the neuron is non-selective because the synaptic weights are all equal. It thus fires periodically, both inside and outside the pattern. (b) At t≈13.5 s, after about 70 pattern presentations and 700 discharges, selectivity to the pattern is emerging: gradually the neuron almost stops discharging outside the pattern (no false alarms), while it does discharge most of the time the pattern is present (high hit rate), here even twice (c) End of the simulation. The system has converged (by saturation). Postsynaptic spike latency is about 4 ms. Hit rate is 99.1% with no false alarms (estimated on the last 150 s).

• It is therefore necessary to use some pre-computed spontaneous activity prepared earlier, found in the file spont_100s_alt.npy.
• It contains 100s of pseduo-random, spontaneous activity for us to use in our simulations.
• Warning, it is a large file at ~1.6GB!

Now we are ready to use these spike trains to train a postsynaptic neuron! ... or are we?

• Creating a model conceptually or mathematically is just the first step.
• Next we have to figure out how to simulate it computationally.

NEST simulation¶

NEST contains many STDP synapse rules. Which one should we use?

• We said earlier that we will use an additive/exponential STDP rule, however that is not the only parameter to consider.
• Another consideration is "how to pair two continuous spikes trains" such that we can apply STDP appropriately to all presynaptic spikes $j$ coming to the postsynaptic neuron $i$.
• A list of STDP models implemented in NEST can be found here: https://nest-simulator.readthedocs.io/en/latest/models/stdp.html
• The following models correspond to the below figure for pairing of spikes for STDP:
  • stdp_nn_symm_synapse (panel A)
  • stdp_nn_pre-centered_synapse (panel B)
  • stdp_nn_restr_synapse (panel C)

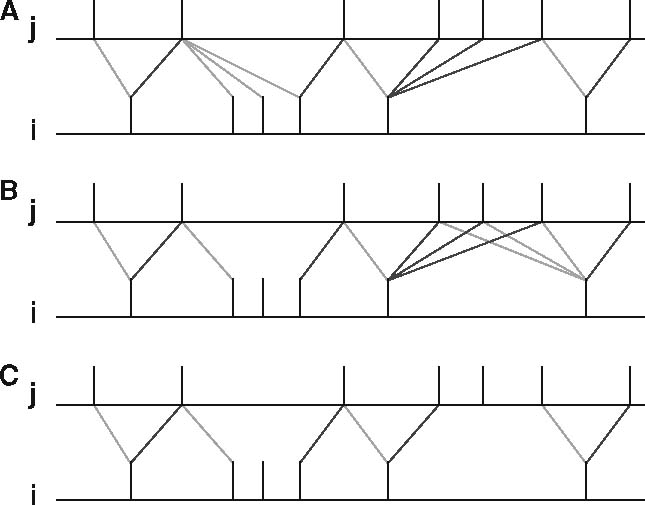Figure 7 from Morrison et al. 2008. Examples of nearest neighbor spike pairing schemes for a presynaptic neuron j and a postsynaptic neuron i. In each case, the dark gray indicate which pairings contribute toward depression of a synapse, and light gray indicate which pairings contribute toward potentiation.