※実装時のパラメータ¶
PairHMMによるアラインメントを実装していく。なお、(kerasy.Bio.alignment.PairHMM)に定義してあります。
In [1]:
from kerasy.Bio.alignment import PairHMM
In [2]:
# サンプル配列
seqX = "CCAGAGCTGTGGCAGACAGTGGCT"
seqY = "CCAGCTGTGCAGACACTGGCTT"
In [3]:
model = PairHMM()
In [4]:
! cat params.json
In [5]:
model.set_params(path="params.json")
Pair HMM とその利点
- HMMのために開発されたアルゴリズムを使える。(らしい←正解ラベルの無いアラインメントでBaum-Welchアルゴリズムをどのように使うのかは現在考察中です。)
- アラインメントの確率的な解釈が可能になる。
グローバルアラインメントを出力する Pair-HMM¶
- Mは $x$ と $y$ がマッチした状態。($x_i$ と $y_j$ がアライン)
- Xは $x$ に挿入が起きている状態。($x_i$ と $-$ がアライン)
- Yは $x$ に欠失が起きている状態。($-$ と $y_j$ がアライン)
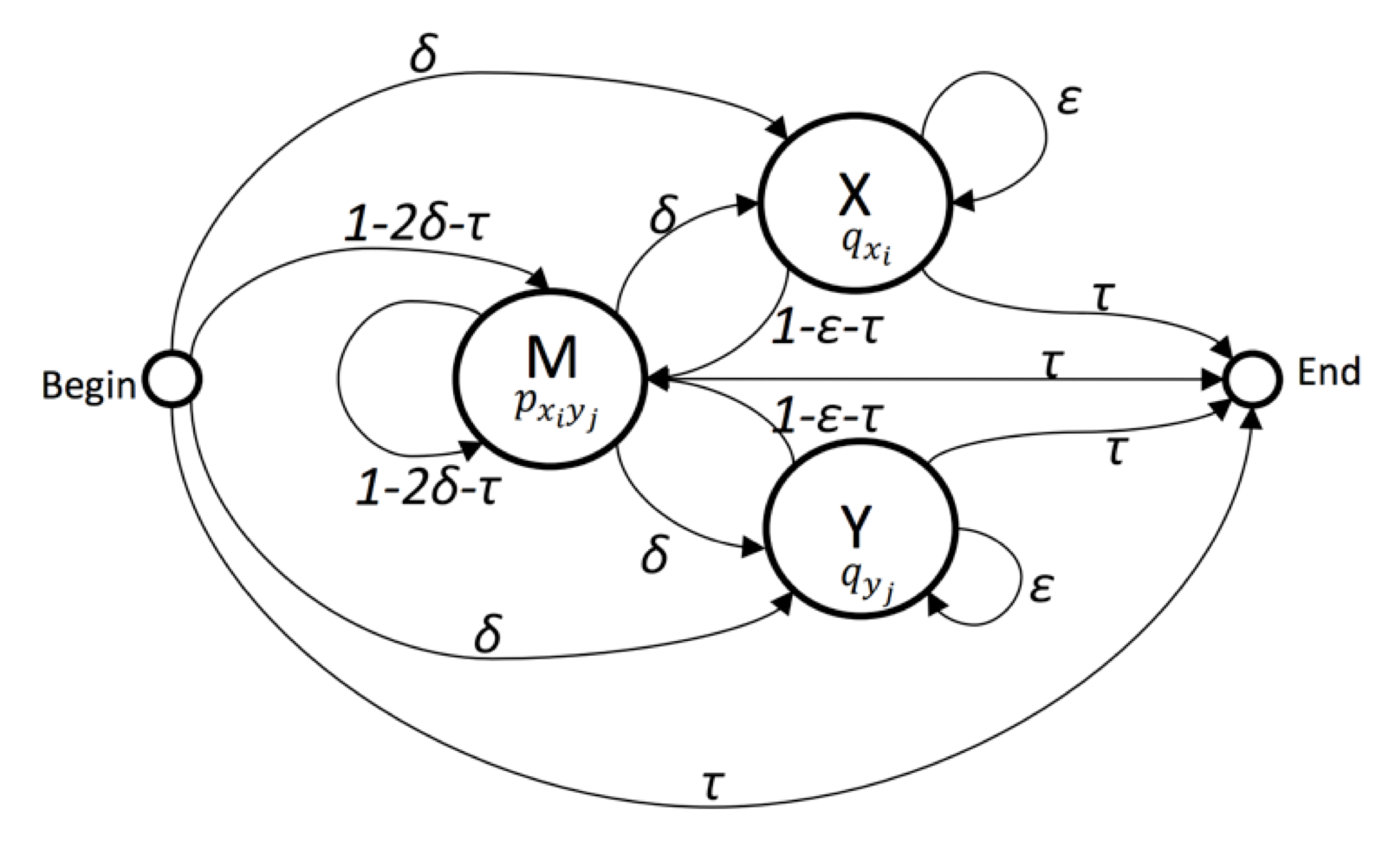
Pair HMMのためのViterbiアルゴリズム¶
2本数の配列 $x,y$ を与えると確率最大のアラインメントを求めるアルゴリズム。
Initialization:¶
$$ \begin{cases} V^M(0,0)=1, V^M(i,0)=V^M(0,j)=0\text{ for }i\neq0,j\neq0\\ V^X(0,0)=0, V^X(1,0)=\delta q_{x_1} V^X(i,0)=\varepsilon q_{x_i}V^X(i-1,0) \text{ for }i=2,\ldots,n\\ V^Y(0,0)=0, V^Y(0,1)=\delta q_{y_1} V^Y(0,j)=\varepsilon q_{y_j}V^Y(0,j-1) \text{ for }j=2,\ldots,m\\ \end{cases} $$Recursion: $i=1,\ldots,n,\quad j=1,\ldots,m$¶
$$ \begin{aligned} V^M(i,j) &= p_{x_iy_j}\max\begin{cases}(1-2\delta-\tau)V^M(i-1,j-1)\\(1-\varepsilon-\tau)V^X(i-1,j-1)\\(1-\varepsilon-\tau)V^Y(i-1,j-1)\end{cases}\\ V^X(i,j) &= q_{x_i}\max\begin{cases}\delta V^M(i-1,j)\\\varepsilon V^X(i-1,j)\end{cases}\\ V^Y(i,j) &= q_{y_j}\max\begin{cases}\delta V^M(i,j-1)\\\varepsilon V^X(i,j-1)\end{cases}\\ \end{aligned} $$Termination:¶
$$v_e = \tau\max\left(V^M(n,m),V^X(n,m),V^Y(n,m)\right)$$In [6]:
P_optimal = model.align(seqX,seqY,return_score=True)
In [7]:
print(f"π*={P_optimal}")
アラインメントの信頼性¶
配列 $x,y$ が与えられた時、アラインメント $\pi$ が得られる条件付き確率を考えることができ、それがアラインメントの信頼度を表していると考ることができる。
$$ P(\pi|x,y) = \frac{P(x,y,\pi)}{P(x,y)}\\ P(x,y) = \sum_{\text{alignments }\pi}P(x,y,\pi) $$※ なお、ここで $P(x,y)$ は $x,y$ に関する全ての可能なアラインメントについて確率を足し合わせたものであり、Forwardアルゴリズムで計算することができる。
Pair HMMのためのForwardアルゴリズム¶
※ Viterbiの $\max$ を $\text{sum}$ に変更しただけ。
Initialization:¶
$$ \begin{cases} F^M(0,0)=1, F^M(i,0)=F^M(0,j)=0\text{ for }i\neq0,j\neq0\\ F^X(0,0)=0, F^X(1,0)=\delta q_{x_1} F^X(i,0)=\varepsilon q_{x_i}F^X(i-1,0) \text{ for }i=2,\ldots,n\\ F^Y(0,0)=0, F^Y(0,1)=\delta q_{y_1} F^Y(0,j)=\varepsilon q_{y_j}F^Y(0,j-1) \text{ for }j=2,\ldots,m\\ \end{cases} $$Recursion: $i=1,\ldots,n,\quad j=1,\ldots,m$¶
$$ \begin{aligned} F^M(i,j) &= p_{x_iy_j}\text{sum}\begin{cases}(1-2\delta-\tau)F^M(i-1,j-1)\\(1-\varepsilon-\tau)F^X(i-1,j-1)\\(1-\varepsilon-\tau)F^Y(i-1,j-1)\end{cases}\\ F^X(i,j) &= q_{x_i}\text{sum}\begin{cases}\delta F^M(i-1,j)\\\varepsilon F^X(i-1,j)\end{cases}\\ F^Y(i,j) &= q_{y_j}\text{sum}\begin{cases}\delta F^M(i,j-1)\\\varepsilon F^X(i,j-1)\end{cases}\\ \end{aligned} $$Termination:¶
$$F_e = \tau\ \text{sum}\left(F^M(n,m),F^X(n,m),F^Y(n,m)\right)$$In [8]:
F,P_all = model.forward(seqX,seqY)
In [9]:
print(f"𝐹^𝐸(𝑛,𝑚)=𝑃(𝑥,𝑦)=Σalignments𝜋𝑃(𝑥,𝑦,𝜋)={P_all}")
In [10]:
print(f"P(π*|x, y)={P_optimal/P_all}")
$x_i$ と $y_j$ がアラインされる確率¶
- 次の式で表される。 $$ \begin{aligned} P(x_i\diamondsuit y_i|x,y) &= \frac{\sum_{\pi\in\Omega_{ij}}P(x,y,\pi)}{P(x,y)}\\ &= \frac{F^M(i,j)\cdot B^M(i,j)}{P(x,y)} \end{aligned}$$
※ $\Omega_{ij}$:$x_i$ と $y_j$ がアラインされるアラインメントの集合
Pair HMMのためのBackwardアルゴリズム¶
Needleman-Wunsh-Gotoh のBackwardアルゴリズムとの類似性に注目!
Initialization:¶
$$ \begin{cases} B^M(n,m)=B^X(n,m)=B^Y(n,m)=\tau\\ B^X(i,m)=\varepsilon q_{x_{i+1}}B^X(i+1,m)\text{ for }i=n-1,\ldots,1\\ B^Y(i,m)=\varepsilon q_{y_{j+1}}B^X(n,j+1)\text{ for }j=m-1,\ldots,1\\ B^M(i,m)=\delta q_{x_{i+1}}B^X(i+1,m)\text{ for }i=n-1,\ldots,1\\ B^M(n,j)=\delta q_{y_{j+1}}B^Y(n,j+1)\text{ for }j=m-1,\ldots,1\\ \end{cases} $$Recursion: $i=n-1,\ldots,1,\quad j=m-1,\ldots,1$¶
$$ \begin{aligned} B^M(i,j) &= \text{sum}\begin{cases}(1-2\delta-\tau)p_{x_iy_j}B^M(i+1,j+1)\\\delta q_{x_{i+1}}B(i+1,j)\\\delta q_{y_{j+1}}B^Y(i,j+1)\end{cases}\\ B^X(i,j) &= (1-\varepsilon-\tau)p_{x_{i+1},y_{j+1}}B^M(i+1,j+1) + \varepsilon q_{x_{i+1}}B^X(i+1,j)\\ B^Y(i,j) &= (1-\varepsilon-\tau)p_{x_{i+1},y_{j+1}}B^M(i+1,j+1) + \varepsilon q_{y_{j+1}}B^Y(i,j+1)\\ \end{aligned} $$In [11]:
B = model.backward(seqX,seqY)
In [12]:
Pij = (F*B)/P_all
In [13]:
import seaborn as sns
import matplotlib.pyplot as plt
In [14]:
sns.heatmap(Pij)
plt.show()
In [15]:
# 可視化のために pandas を使用。
import pandas as pd
r,c = Pij.shape
pd.set_option('display.max_rows', r)
pd.set_option('display.max_columns', c)
In [16]:
df = pd.DataFrame(Pij)
In [17]:
df
Out[17]:
In [ ]: