- 講師:杉山将
- 講師:本多淳也
- 参考書:エージェントアプローチ人工知能 第2版
- 参考書:イラストで学ぶ 人工知能概論
回帰
回帰の目標は、「訓練標本から真の関数にできるだけ近い関数を求めること」である。
モデル
- モデル:学習結果の関数を探す候補集合。パラメータ $\boldsymbol{\theta}$ の値を指定すると関数が一つ決まる。
$$\left\{f_{\boldsymbol{\theta}}(\mathbf{x}) | \boldsymbol{\theta} = (\theta_1,\ldots,\theta_b)^T\right\}$$
- 線形モデル:$f_{\boldsymbol{\theta}}(\mathbf{x})$ が「 $\boldsymbol{\theta}$ に関して」 線形 $$f_{\boldsymbol{\theta}}(\mathbf{x}) = \sum_{j=1}^b\theta_j\phi_j(\mathbf{x})\quad \mathbf{x}\in\mathbb{R}^d$$
- 非線形モデル:それ以外。
カーネルモデル¶
$$f_{\boldsymbol{\theta}}\mathbf{x}) = \sum_{j=1}^n\theta_jK(\mathbf{x},\mathbf{x}_j)$$- 線形モデルの一種。
- 基底関数が入力に依存する。
- $K(\mathbf{x},\mathbf{c})$ はカーネル関数であり、$\phi_j(\cdot) = K(\cdot,\mathbf{x}_j)$ に対応する。(入力に依存している!!)
- カーネル関数として最も一般的なものはガウスカーネル
- ガウス関数を各訓練入力標本の場所に配置 $$K(\mathbf{x},\mathbf{c}) = \exp\left(-\frac{\|\mathbf{x}-\mathbf{c}\|^2}{2h^2}\right),\quad h(>0)$$
- 訓練標本が入力空間上に偏って分布している時、ガウスカーネルモデルは訓練入力標本が存在しない領域を無視する関数が学習される。→ある種の次元削減効果が得られる(?)
最小二乗回帰
訓練出力との二乗誤差を最小にすることを目的とした回帰。
$$\min_{\boldsymbol{\theta}}\left[\frac{1}{2}\sum_{i=1}^n\left(y_i-f_{\boldsymbol{\theta}}(\mathbf{x}_i)\right)^2\right]$$正則化最小二乗回帰
過学習を抑えるため、「回帰係数 $\boldsymbol{\theta}$ の各要素の絶対値が大きくなることに罰則を加えた」最小二乗回帰。
$$\min_{\boldsymbol{\theta}}\left[\frac{1}{2}\sum_{i=1}^n\left(y_i-f_{\boldsymbol{\theta}}(\mathbf{x}_i)\right)^2 + \frac{\lambda}{2}\sum_{j=1}^n\theta_j^2\right]\quad \lambda>0$$交差確認法
正則化パラメータ $\lambda$ や、ガウスカーネルのバンド幅 $h$ などは、設計者が 独断で決定する。
より汎化性能の高いモデルを選択するため、訓練標本を $k$ 分割し、「そのうち一つを検証用。残りを訓練用」に分ける方法が一般的。この作業を $k$ 回繰り返して平均スコアを比較する。
分類
分類の目標は、「クラス間の分離境界を求めること」である。
超平面分類器
標本空間を超平面 $f_{\mathbf{w},b} = \mathbf{w}^T\mathbf{x} + b = 0$ で分離する。
サポートベクトルマシン
- 二つのクラスを分類する超平面はいくつかあるが、「二つのクラス間の隙間(マージン)の大きさが最大」なものが汎化性能が高いという考えから マージン最大化 を目標とする手法。
- 標本が線形分離可能でない時には、マージンを定義することができないので、標本毎に少しの誤差 $\xi_i$ を許す。 $$ \begin{aligned} \min_{\mathbf{w},b,\boldsymbol{\xi}} \quad&\|\mathbf{w}\|^2 + C\sum_{i=1}^n\xi_i,\quad f_{\mathbf{w},b}(\mathbf{x}) = \mathbf{w}^T\mathbf{x} + b\\ \text{subject to }\quad&y_if_{\mathbf{w},b}(\mathbf{x}_i)\geq1-\xi_i\Longleftrightarrow\xi_i\geq1-y_if_{\mathbf{w},b}(\mathbf{x}_i)\\ &\xi_i\geq0\quad\text{for $i=1,\ldots,n$} \end{aligned} $$
- $\xi_i$ が小さいほど目的関数が減るので、結局必要な計算は $$\min_{\mathbf{w},b}\left[\|\mathbf{w}\|^2 + C\sum_{i=1}^n\max\left\{0,1-y_if_{\mathbf{w},b}(\mathbf{x}_i)\right\}\right]$$
非線形化
非線形関数 $\phi(\mathbf{x})$ で標本を特徴空間へ写像し、特徴空間内でマージン最大の超平面を求める。
$$f_{\mathbf{w},b}(\mathbf{x}) = \mathbf{w}^T\mathbf{x} + b \rightarrow f_{\mathbf{w},b}(\mathbf{x}) = \mathbf{w}^T\phi(\mathbf{x}) + b$$これをそのまま解く場合 $\phi(\mathbf{x})$ の次元が大きい場合は計算が大変なので、カーネルトリックを用いる。
カーネルトリック¶
- 線形モデルにおける多くの回帰・分類手法では、特徴量 $\phi(\mathbf{x}_i)$ を直接求めなくても、その内積 $\phi(\mathbf{x}_i)^T\phi(\mathbf{x}_j)$ さえわかれば実装可能。
- → 特徴空間上の内積をカーネル関数で直接表現する。
- 計算量が特徴空間の次元によらない!
- 【サポートベクターマシンの場合】
- 仮定: $$\mathbf{w}=\sum_{j=1}^n\theta_j\phi(\mathbf{x}_j),b=0$$
- 最小化したい目的関数は、以下の形で表される。 $$ \begin{cases} \begin{aligned} &\min_{\mathbf{w},b}\left[\|\mathbf{w}\|^2 + C\sum_{i=1}^n\max\left\{0,1-y_if_{\mathbf{w},b}(\mathbf{x_i})\right\}\right]\\ &f_{\mathbf{w},b}(\mathbf{x}) = \mathbf{w}^T\phi(\mathbf{x}) + b \end{aligned} \end{cases} \rightarrow \begin{cases} \begin{aligned} &\min_{\boldsymbol{\theta}}\left[\boldsymbol{\theta}^T\mathbf{K}\boldsymbol{\theta} + C\sum_{i=1}^n\max\left\{0,1-y_if_{\mathbf{w},b}(\mathbf{x_i})\right\}\right]\\ &f_{\mathbf{w},b}(\mathbf{x}) = \sum_{j=1}^n\theta_jK(\mathbf{x},\mathbf{x}_j),\quad\phi(\mathbf{x}_i)^T\phi(\mathbf{x}_j) = K(\mathbf{x}_i,\mathbf{x}_j) \end{aligned} \end{cases} $$
最適化
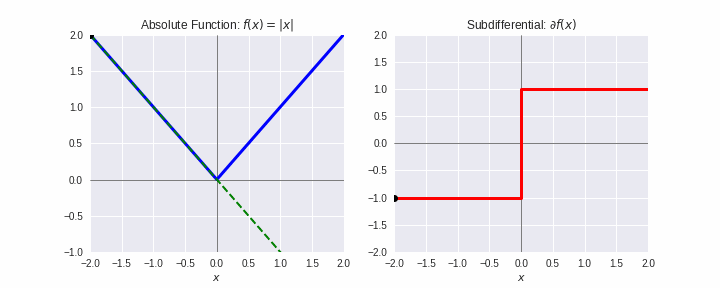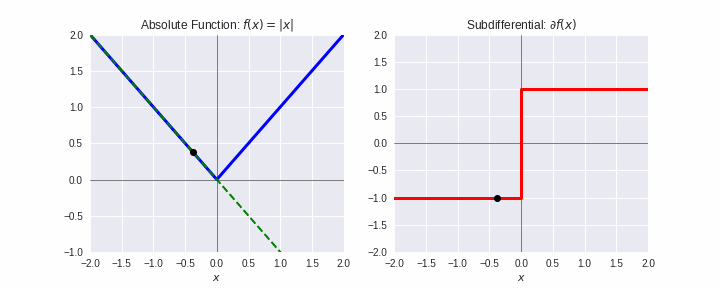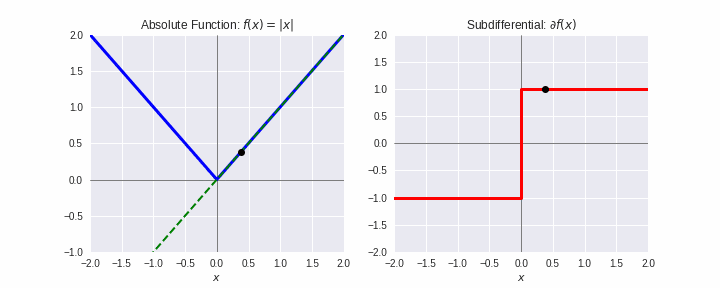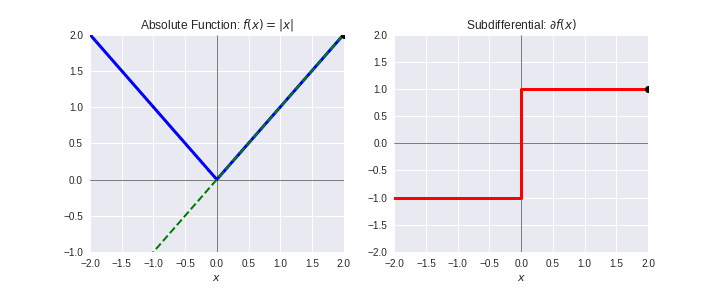
劣勾配¶
- 凸関数 $f$ の $\mathbf{x}^{\prime}$ での劣勾配(sub-gradient)とは、全ての $\mathbf{x}\in\mathbb{R}^d$ に対して次式を満たす $\boldsymbol{\xi}$:
$$f(\mathbf{x}) \geq f(\mathbf{x^{\prime}}) + \boldsymbol{\xi}^T(\mathbf{x}-\mathbf{x}^{\prime})$$
- $f$ が微分可能なとき、$\boldsymbol{\xi} = \nabla f(\mathbf{x}^{\prime})$
- 上式を満たす $\boldsymbol{\xi}$ 全体を $\partial f(\mathbf{x}^{\prime})$ で表し、劣微分(sub-differential)とよぶ。
- 劣勾配法:勾配法において、微分不可能な点では、劣微分のどれかの値を用いる。
サポートベクトルマシン¶
※ 仮定:$\mathbf{w}=\sum_{j=1}^n\theta_j\phi(\mathbf{x}_j),b=0$
$$
\begin{cases}
\begin{aligned}
&\min_{\boldsymbol{\theta}}\left[\boldsymbol{\theta}^T\mathbf{K}\boldsymbol{\theta} + C\sum_{i=1}^n\max\left\{0,1-y_if_{\mathbf{w},b}(\mathbf{x_i})\right\}\right]\\
&f_{\mathbf{w},b}(\mathbf{x}) = \sum_{j=1}^n\theta_jK(\mathbf{x},\mathbf{x}_j),\quad\phi(\mathbf{x}_i)^T\phi(\mathbf{x}_j) = K(\mathbf{x}_i,\mathbf{x}_j)
\end{aligned}
\end{cases}
$$
$\min$ の中身を劣微分すれば、
$$ \partial_{\theta_j}\max\left(0, 1-f_{\boldsymbol{\theta}}(\mathbf{x}_i)y_i\right)= \begin{cases} \begin{aligned} &-y_iK(\mathbf{x}_i,\mathbf{x}_j) & \left(\text{if $1-f_{\boldsymbol{\theta}}(\mathbf{x}_i)y_i > 0$ }\right)\\ &0 & (\text{otherwise.}) \end{aligned} \end{cases} $$となるので、劣勾配法による実装時は以下で表せる。
$$\boldsymbol{\theta}\longleftarrow\boldsymbol{\theta} - \varepsilon\left(C\sum_{i=1}^n\partial_{\boldsymbol{\theta}}\max\left(0,1-f_{\boldsymbol{\theta}}(\mathbf{x}_i)y_i\right) + 2\mathbf{K}\boldsymbol{\theta}\right)$$まとめ¶
- 教師付き学習:訓練データ(入出力の組)から、その背後に潜む関数を学習
- 回帰も分類も、「損失*正則化(regularization)」の最小化を目標としている。 $$\min_{\boldsymbol{\theta}}\left[\sum_{i=1}^n\text{loss}\left(f_{\boldsymbol{\theta}}(\mathbf{x}_i),y_i\right) + \lambda\text{Reg}(\boldsymbol{\theta})\right]$$
In [ ]: