In [1]:

import numpy as np
import matplotlib.pyplot as plt

Section5.1 Bayesian Model Comparison¶

Overfitting¶

In [2]:

N = 15
Ms = [2,4,8,16]
seed = 0

In [3]:

# Training data.
x = np.random.RandomState(seed).uniform(low=0, high=1, size=N)
Noise = np.random.RandomState(seed).normal(loc=0, scale=0.1, size=N)
t = np.sin(2*np.pi*x) + Noise

In [4]:

fig=plt.figure(figsize=(12,8))
for i,M in enumerate(Ms):
    ax=fig.add_subplot(2,2,i+1)
    # Training.
    X = np.array([x**m for m in range(M+1)]).T
    w = np.linalg.solve(X.T.dot(X), X.T.dot(t))
    # For Validation plot.
    Xs = np.linspace(0,1,1000)
    t_true = np.sin(2*np.pi*Xs)
    t_pred = w.dot(np.array([Xs**m for m in range(M+1)]))
    # RSS(Residual Sum of Squares)
    residual = t - w.dot(np.array([x**m for m in range(M+1)]))
    RSS = residual.T.dot(residual)
    # Plot.
    ax.plot(Xs,t_true,color="black", label="$t=\sin(2\pi x)$")
    ax.plot(Xs,t_pred,color="red", label=f"prediction ($M={M}$)")
    ax.scatter(x,t,edgecolors='blue',facecolor="white",label="train data")
    ax.set_title(f"Results (RSS=${RSS:.3f}$,M=${M}$)"), ax.set_xlabel("$x$"), ax.set_ylabel("$t$")
    ax.set_xlim(0,1), ax.set_ylim(-1.2,1.2)
    ax.legend()
plt.tight_layout()
plt.show()

Varying Component Number¶

In [5]:

from kerasy.ML.MixedDistribution import MixedGaussian
from kerasy.utils.data_generator import generateMultivariateNormal

In [6]:

N = 200
cls = 6
seed = 123

In [7]:

data,means = generateMultivariateNormal(cls=cls, N=N, scale=8e-3, same=False, seed=seed)
x,y = data.T
mux, muy = means.T

In [8]:

# Background Color
xmin,ymin = np.min(data, axis=0); xmax,ymax = np.max(data, axis=0)
Xs,Ys = np.meshgrid(np.linspace(xmin, xmax, 100), np.linspace(ymin, ymax, 100))
XYs = np.c_[Xs.ravel(),Ys.ravel()]

In [9]:

Nfig = cls
col = 3
row = Nfig//col+1 if Nfig%col != 0 else Nfig//col
fig = plt.figure(figsize=(6*col,4*row))

Likelihoods = []
for i,K in enumerate(range(1,cls+1)):
    ax = fig.add_subplot(row,col,i+1)
    model = MixedGaussian(K=K, random_state=seed)
    model.fit(data, span=20)
    Z = model.predict(XYs)
    idx = np.argmax(model.predict(data), axis=1)
    Zs = np.sum(Z, axis=1).reshape(Xs.shape) # Likelihood.
    likelihood = np.sum(Z)
    ax.scatter(x,y,c=idx)
    ax.pcolor(Xs, Ys, Zs, alpha=0.2)
    ax.set_xlim(xmin, xmax)
    ax.set_ylim(ymin, ymax)
    ax.set_title(f"K={K}, {np.sum(Z):.1f}")
    Likelihoods.append(likelihood)
plt.tight_layout()
plt.show()

In [10]:

fig = plt.figure(figsize=(12,4))
axL = fig.add_subplot(1,2,1)
axL.scatter(x,y, label="data")
axL.scatter(mux,muy, label="mean", marker="*", color="red", s=150)
axL.set_title("Training Data.")
axL.legend()

axR = fig.add_subplot(1,2,2)
axR.plot(np.arange(cls)+1,Likelihoods)
axR.scatter(np.arange(cls)+1, Likelihoods)
axR.set_xlabel("num comp")
axR.set_ylabel("likelihoods")
axR.set_title("Log likelihood vs num comp", fontsize=18)

plt.tight_layout()
plt.show()

Cross Validation¶

※ Not Bayesian

estimate the skill of a machine learning model on unseen data.
use a limited sample in order to estimate how the model is expected to perform in general when used to make predictions on data not used during the training of the model.

In [11]:

n_fold = 5
size = N//n_fold
Kmax = 30

In [12]:

Likelihoods = []
CrossValidationLikelihoods = []
for i,K in enumerate(range(1,Kmax+1)):
    H = 0
    for h in range(n_fold):
        mask = np.ones(shape=N, dtype=bool)
        mask[h*size:(h+1)*size] = False
        model = MixedGaussian(K=K, random_state=seed)
        model.fit(data[mask], span=20)
        Z = model.predict(data[np.logical_not(mask)])
        H += np.sum(Z)
    model = MixedGaussian(K=K, random_state=seed)
    model.fit(data, span=20)
    Z = model.predict(data)
    Likelihoods.append(np.sum(Z))
    CrossValidationLikelihoods.append(H)

In [13]:

fig = plt.figure(figsize=(12,4))
axL = fig.add_subplot(1,2,1)
axL.plot(np.arange(Kmax)+1, CrossValidationLikelihoods)
axL.scatter(np.arange(Kmax)+1, CrossValidationLikelihoods)
axL.set_xlabel("num comp"), axL.set_ylabel("Cross Validation likelihoods"), axL.set_title("Cross Validation Log likelihood vs num comp", fontsize=18)

axR = fig.add_subplot(1,2,2)
axR.plot(np.arange(Kmax)+1, Likelihoods)
axR.scatter(np.arange(Kmax)+1, Likelihoods)
axR.set_xlabel("num comp"), axR.set_ylabel("likelihoods"), axR.set_title("Log likelihood vs num comp", fontsize=18)

plt.tight_layout()
plt.show()

Cross Entropy of Prediction¶

※ Not Bayesian

empirical distribution¶

$D = \left\{\mathbf{x}^{(h)}|h=1,\ldots,n\right\}$
$x\sim\mathrm{Emp}(D)$
$f_X(\mathbf{X}) = \frac{1}{n}\sum_{h=1}^n\delta\left(\mathbf{x}-\mathbf{x}^{(h)}\right)$
$\mathbb{E}\left(g(\mathbf{x})\right) = \frac{1}{n}\sum_{h=1}^n\int d\mathbf{x}g(\mathbf{x})\delta\left(\mathbf{x}-\mathbf{x}^{(h)}\right) = \frac{1}{n}\sum_{h=1}^ng\left(\mathbf{x}^{(h)}\right)$

In [14]:

seed = 0
N = 1000

In [15]:

data = np.random.RandomState(seed).normal(size=N)

In [16]:

Emp = dict(zip(data,np.zeros(N)))
for x in data: Emp[x] += 1/N

In [17]:

for X,Y in sorted(Emp.items()):
    plt.plot((X,X),(0,Y), color="black", alpha=0.1)
plt.title("Empirical distribution (Normal)")
plt.xlabel("x")
plt.show()

We can assume Empirical distribution as a true distribution.

Cross Entropy¶

$$ \begin{aligned} H(D,\boldsymbol{\theta}) &= \text{Cross Entropy between }f_{\text{Emp}(D)} \text{ and }f\left(\mathbf{x}|\boldsymbol{\theta}\right)\\ &= \mathbb{E}_{\text{Emp}(D)}\left(-\log f\left(\mathbf{X}|\boldsymbol{\theta}\right)\right)\\ &= -\int f_{\text{Emp}(D)}(\mathbf{x})\log f\left(\mathbf{x}|\boldsymbol{\theta}\right)d\mathbf{x}\\ &= -\frac{1}{n}\sum_{h=1}^n\log f\left(\mathbf{x}^{(h)}|\boldsymbol{\theta}\right)\\ &= -\bar{l}^{(n)}\left(\mathbf{x}|\boldsymbol{\theta}\right) \end{aligned} $$

We can also say that:

$$ \begin{aligned} H(D,\boldsymbol{\theta}) &= -\int f_{\text{Emp}}(\mathbf{x})\log f\left(\mathbf{x}|\boldsymbol{\theta}\right)d\mathbf{x}\\ &\Rightarrow \int f_{\text{Emp}}(\mathbf{x})\log f_{\text{Emp}}(\mathbf{x})d\mathbf{x} -\int f_{\text{Emp}}(\mathbf{x})\log f\left(\mathbf{x}|\boldsymbol{\theta}\right)d\mathbf{x}\\ &= -\int f_{\text{Emp}}(\mathbf{x})\log\left\{\frac{f_{\text{Emp}}(\mathbf{x})}{f\left(\mathbf{x}|\boldsymbol{\theta}\right)}\right\}d\mathbf{x}\\ &= \mathrm{KL}\left(f_{\text{Emp}}\|f\left(\mathbf{x}|\boldsymbol{\theta}\right)\right)\\ &= \text{Kullback-Leibler divergence between}f_{\text{Emp}(D)} \text{ and }f\left(\mathbf{x}|\boldsymbol{\theta}\right) \end{aligned} $$

Evidence Approximation¶

※ Yes Bayesian

In a fully Bayesian treatment of the linear basis function model, we would introduce prior distributions over the hyperparameters $\alpha$, and $\beta$. $$ \begin{aligned} p(t|\mathbf{t},\mathbf{X},\mathbf{x},\alpha,\beta) &= \int p(t|\mathbf{w},\mathbf{x},\beta)p(\mathbf{w}|\mathbf{t},\mathbf{X},\alpha,\beta)d\mathbf{w}& (3.57)\\ &\Rightarrow \int p(t|\mathbf{w},\mathbf{x},\beta)p(\mathbf{w}|\mathbf{t},\mathbf{X},\alpha,\beta)p(\alpha,\beta|\mathbf{t},\mathbf{X})d\mathbf{w}d\alpha d\beta& (3.74) \end{aligned} $$
Marginalize with respect to these hyperparameters as well as with respect to the parameters $\mathbf{w}$ to make predictions.
Complete marginalization over all of these variables is analytically intractable.
We will maximize $(3.74)$ in line with the framework of empirical Bayes (or type 2 maximum likelihood, generalized maximum likelihood, evidence approximation)
1. Obtain the marginal likelihoo function by first integrating over the parameters $\mathbf{w}$ $$p(\mathbf{t}|\alpha,\beta) = \int p(\mathbf{t}|\mathbf{w},\mathbf{X},\beta)p(\mathbf{w}|\alpha)d\mathbf{w}\qquad (3.77)$$
2. Maximize $p(\mathbf{t}|\alpha,\beta)$ with respect to $\alpha$ and $\beta$.

In [18]:

from kerasy.utils.preprocessing import PolynomialBaseTransformer
from kerasy.utils.data_generator import generateSin, generateGausian
from kerasy.ML.linear import EvidenceApproxBayesianRegression

In [19]:

N = 20
Ms = np.arange(10)
xmin=0; xmax=1 
seed = 0

In [20]:

x_train,y_train = generateSin(size=N, xmin=xmin,xmax=xmax,seed=seed)
_,      y_noise = generateGausian(size=N, x=x_train, loc=0, scale=0.15, seed=seed)
y_train += 1+y_noise

In [21]:

alpha = 100
beta = 100

In [22]:

evidences = []
history = []
for M in Ms:
    phi = PolynomialBaseTransformer(M=M)
    x_train_features = phi.transform(x_train)
    model = EvidenceApproxBayesianRegression(alpha=alpha, beta=beta, iter_max=10000)
    model.fit(x_train_features,y_train)
    evidences.append(model.evidence(x_train_features, y_train))
    history.append(model)
best_M = np.argmax(evidences[1:])+1
best_model = history[best_M]

In [23]:

x_test = np.linspace(xmin,xmax,1000)
phi = PolynomialBaseTransformer(M=best_M)
x_test_features = phi.transform(x_test)
y_test = 1+np.sin(2*np.pi*x_test)
y_pred,y_std = best_model.predict(x_test_features)

In [24]:

fig = plt.figure(figsize=(12,4))
axEVI = fig.add_subplot(1,2,1)
axEVI.plot(Ms, evidences)
axEVI.scatter(Ms, evidences)
axEVI.set_title("The relationship between 'model evidence' and $M$"), axEVI.set_xlabel("$M$"),axEVI.set_ylabel("$\log({model\ evidence})$", fontsize=16)

axBest = fig.add_subplot(1,2,2)
axBest.plot(x_test,y_test,color="black", label="$\sin(2\pi x)$")
axBest.plot(x_test,y_pred,color="red", label="predict($\mu$)")
axBest.fill_between(x_test, y_pred-y_std, y_pred+y_std, color="pink", alpha=0.5)
axBest.scatter(x_train,y_train,s=50,edgecolors='black',facecolor="white",label="train data")
axBest.set_ylim(-0.5,2.5), axBest.legend(), axBest.set_title(f"Bayesian Linear Regression (M={best_M})")

plt.tight_layout()
plt.show()

In [25]:

print("[Best Parameter]")
print(f"M     = {best_M}")
print(f"alpha = {best_model.alpha}")
print(f"beta  = {best_model.beta}")

[Best Parameter]
M     = 3
alpha = 0.0025750535934692723
beta  = 56.07833727501231

Section5.2 Markov Process¶

Biological Diversity
Single Origin of Life
"Nothing in Biology Makes Sense Except in the Light of Evolution" C.T. Dobzhansky
Stochastic Transcription (Stochasticity vs Regulation)
Stochasticity in Development

Stochastic Process¶

Mathematical description of stochastic behaviors.

data: $\left\{\mathbf{X}_t|t=1,\ldots,n\right\}$
Probability: $\mathbb{P}\left(\mathbf{X}_{t_m} = \mathbf{x}_{t_m},\ldots,\mathbf{X}_{t_2} = \mathbf{x}_{t_2},\mathbf{X}_{t_1} = \mathbf{x}_{t_1}\right)$

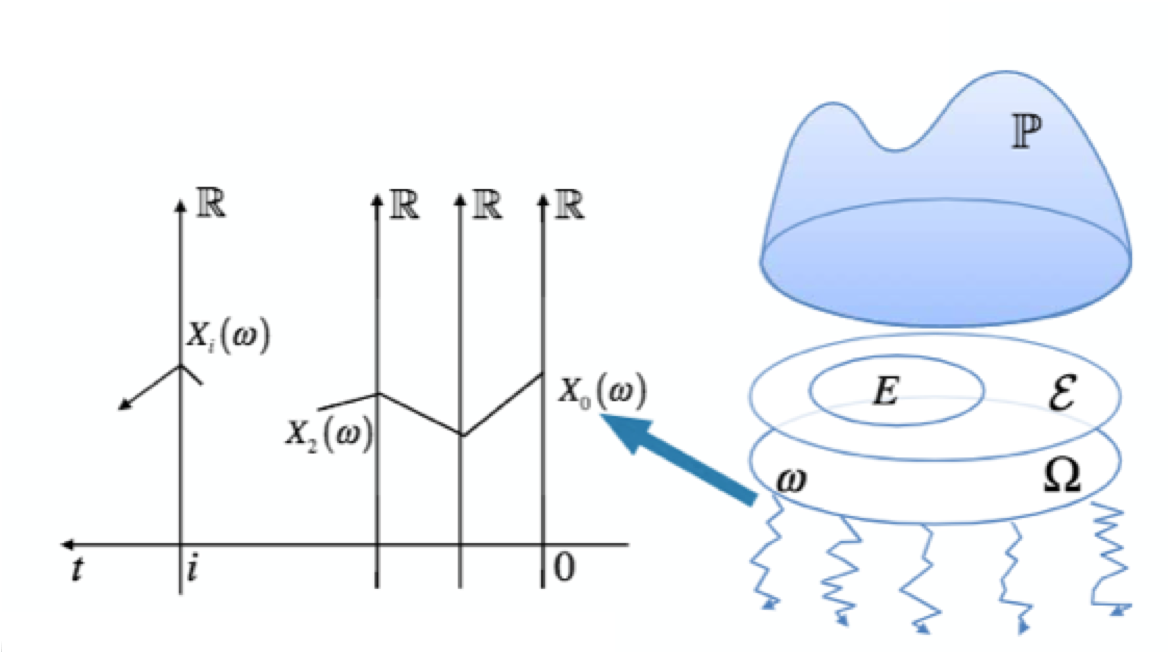
Probability Space

$\omega$ is one of the random paths.
$\mathbf{X}_t$ is a map indicats which state random paths $\omega$ is in at time $t$
Events $E$ is a constraint on the value of $\mathbf{X}_t$ at some times.
$P(E)$ is the probability if the random paths satisfy the constraint $E$.

markov Process¶

$$\mathbb{P}\left(\mathbf{X}_t = \mathbf{x}_t|\mathbf{X}_{t-1} = \mathbf{x}_{t-1},\ldots,\mathbf{X}_0 = \mathbf{x}_0\right) = \mathbb{P}\left(\mathbf{X}_t=\mathbf{x}_t|\mathbf{X}_{t-1}=\mathbf{x_{t-1}}\right)$$

Decomposition of Joint Distribution $$ \begin{aligned} &\mathbb{P}\left(\mathbf{X}_t = \mathbf{x}_t,\mathbf{X}_{t-1} = \mathbf{x}_{t-1},\ldots,\mathbf{X}_0 = \mathbf{x}_0\right)\\ &=\mathbb{P}\left(\mathbf{X}_t = \mathbf{x}_t | \mathbf{X}_{t-1} = \mathbf{x}_{t-1},\ldots,\mathbf{X}_0 = \mathbf{x}_0\right)\times\mathbb{P}\left(\mathbf{X}_{t-1} = \mathbf{x}_{t-1},\ldots,\mathbf{X}_0 = \mathbf{x}_0\right)\\ &=\mathbb{P}\left(\mathbf{X}_t = \mathbf{x}_t | \mathbf{X}_{t-1} = \mathbf{x}_{t-1},\ldots,\mathbf{X}_0 = \mathbf{x}_0\right)\times \mathbb{P}\left(\mathbf{X}_{t-1} = \mathbf{x}_{t-1} | \mathbf{X}_{t-2} = \mathbf{x}_{t-2},\ldots,\mathbf{X}_0 = \mathbf{x}_0\right)\times \mathbb{P}\left(\mathbf{X}_{t-2} = \mathbf{x}_{t-2},\ldots,\mathbf{X}_0 = \mathbf{x}_0\right)\\ &= \mathbb{P}\left(\mathbf{X}_t = \mathbf{x}_t | \mathbf{X}_{t-1} = \mathbf{x}_{t-1},\ldots,\mathbf{X}_0 = \mathbf{x}_0\right)\times \cdots \times\mathbb{P}\left(\mathbf{X}_2=\mathbf{x}_2|\mathbf{X}_1=\mathbf{x}_1,\mathbf{X}_0=\mathbf{x}_0\right)\times \mathbb{P}\left(\mathbf{X}_1=\mathbf{x}_1|\mathbf{X}_0=\mathbf{x}_0\right)\times\mathbb{P}\left(\mathbf{X}_0=\mathbf{x}_0\right)\\ &= \mathbb{P}\left(\mathbf{X}_t = \mathbf{x}_t | \mathbf{X}_{t-1} = \mathbf{x}_{t-1}\right) \times \mathbb{P}\left(\mathbf{X}_{t-1} = \mathbf{x}_{t-1} | \mathbf{X}_{t-2} = \mathbf{x}_{t-2}\right)\times \cdots\times\mathbb{P}\left(\mathbf{X}_1=\mathbf{x}_1|\mathbf{X}_0=\mathbf{x}_0\right)\times\mathbb{P}\left(\mathbf{X}_0=\mathbf{x}_0\right)\quad\left(\because \text{Markov Process}\right) \end{aligned} $$

Transition Matrix (Assume Time Independence): $$P = \left\{P_{ij}\right\} = \left\{\mathbb{P}\left(\mathbf{X}_t=i|\mathbf{X}_{t-1}=j\right)\right\},\quad P_{ij}\geq0,\sum_i P_{ij}=1$$

Computing transition probability¶

Birth and Death process $$ P= \left(\begin{matrix}1-\lambda_0&\mu_1&0&0\\\lambda_0&1-\lambda_1-\mu_1&\mu_2&0\\0&\lambda_1&1-\lambda_2-\mu_2&\mu_3\\0&0&\lambda_2&1-\mu_3\end{matrix}\right) $$

$P = U\Lambda U^{-1}$: Eigen decomposition
$P^n = U\Lambda^n U^{-1}$

In [26]:

def makeRandomP(N, seed=123):
    lambdas = np.r_[np.random.RandomState(seed).uniform(low=0,high=1/N, size=N-1), np.zeros(shape=1)]
    mus = np.r_[np.zeros(shape=1), np.random.RandomState(seed+1).uniform(low=0,high=1/N, size=N-1)] 

    P = np.zeros(shape=(N,N))
    for i in range(N):
        P[i,-1+i]                    = mus[i]; 
        P[i,i]                       = 1-mus[i]-lambdas[i]; 
        P[i,1+i if 1+i<N else 1+i-N] = lambdas[i]
    return P

In [27]:

def LongTimeBehaviors(P,even=True):
    inf=50 if even else 51
    eigenvals,eigenvecs = np.linalg.eig(P)
    Lambda = np.diag(eigenvals)
    eigenvecs_inv = np.linalg.inv(eigenvecs)
    Pn = np.dot(eigenvecs, np.dot(Lambda**inf, eigenvecs_inv))
    Pn = np.where(Pn<1e-5, 0, Pn)
    return Pn

example¶

Periodic¶

In [28]:

P = np.array([
    [0, 1, 0],
    [1/2, 0, 1/2],
    [0, 1, 0]
])

In [29]:

print(f"P^2n: \n{LongTimeBehaviors(P, even=True)}\n")
print(f"P^2n+1: \n{LongTimeBehaviors(P, even=False)}")

P^2n: 
[[0.5 0.  0.5]
 [0.  1.  0. ]
 [0.5 0.  0.5]]

P^2n+1: 
[[0.  1.  0. ]
 [0.5 0.  0.5]
 [0.  1.  0. ]]

Reducible¶

In [30]:

P = np.array([
    [1/3, 3/4, 0, 0],
    [2/3, 1/4, 0, 0],
    [0, 0, 1/3, 3/4],
    [0, 0, 2/3, 1/4]
])

In [31]:

LongTimeBehaviors(P)

Out[31]:

array([[0.52941176, 0.52941176, 0.        , 0.        ],
       [0.47058824, 0.47058824, 0.        , 0.        ],
       [0.        , 0.        , 0.52941176, 0.52941176],
       [0.        , 0.        , 0.47058824, 0.47058824]])

Absorbing¶

In [32]:

P = np.array([
    [1, 1/2, 0, 0],
    [0, 0, 1/2, 0],
    [0, 1/2, 0, 0],
    [0, 0, 1/2, 1]
])

In [33]:

LongTimeBehaviors(P)

Out[33]:

array([[1.        , 0.66666667, 0.33333333, 0.        ],
       [0.        , 0.        , 0.        , 0.        ],
       [0.        , 0.        , 0.        , 0.        ],
       [0.        , 0.33333333, 0.66666667, 1.        ]])

Irreducible, Aperiodic¶

In [34]:

P = np.array([
    [2/3, 1/12,   0],
    [1/3, 5/8,  1/8],
    [0,   7/24, 7/8],
])

In [35]:

LongTimeBehaviors(P)

Out[35]:

array([[0.06976762, 0.06976748, 0.06976741],
       [0.27906992, 0.2790698 , 0.27906974],
       [0.65116246, 0.65116272, 0.65116286]])

In [ ]:

生物統計論第5回

Section5.1 Bayesian Model Comparison¶

Overfitting¶

Varying Component Number¶

Cross Validation¶

Cross Entropy of Prediction¶

empirical distribution¶

Cross Entropy¶

Evidence Approximation¶

Section5.2 Markov Process¶

Stochastic Process¶

markov Process¶

Computing transition probability¶

example¶

Periodic¶

Reducible¶

Absorbing¶

Irreducible, Aperiodic¶

Table of Contents

Published

Last Updated

Category

Tags

Contact

Other contents