生物統計論 第1回

• 講師：木立尚孝

講義概要

1. 09/27 (Fri) 10:25-12:10
2. 10/04 (Fri) 10:25-12:10
3. 10/11 (Fri) 10:25-12:10
4. 10/18 (Fri) 10:25-12:10
5. 10/25 (Fri) 10:25-12:10
6. 11/08 (Fri) 10:25-12:10
7. 11/15 (Fri) 10:25-11:30(Lecture) / 11:30-12:10: (Test)

Section1.1 STATISTICAL ANALYSIS

• Genomic data has recently become available, so the analyzing methods still its infancy at the century scale.
• It is very important how much information can be extracted from genomic and other omic data.
• Data-driven Research
  • Development of measurement, communication, computing technologies.
  • data science, e-science
  • Statistics, computer skill, artificial intelligence, machine learning.
• Statistical Analysis
  • Subjects and measurements are often conclude the random events, such as noise.
  • Aiming for finding the "True" distribution, and inferencing on that distribution.
• Power of Statistical Methods
  • Amount of information we can extract "Many and high" / "Few or low" quality
  • Event infinite number of data cannot answer all questions. ex) we couldn't answer "what is the number of eyes on the next dice."
  • Data dependency.

Section1.2 PROBABILITY DEFINITIONS

• Probability:
  • Mathematical Probability: The probability of an event consisting of n out of m possible equally likely occurrences, defined to be n / m
  • Statistical Probability: Each event is random, but if you repeat it a lot, you can see the probability that each event occurs.
  • Subjective Probability: A type of probability derived from an individual's personal judgment or own experience about whether a specific outcome is likely to occur.
• ※ Mathematical Probability is the most strict and basic.

Probability space \(\left(\Omega, E, P\right)\)

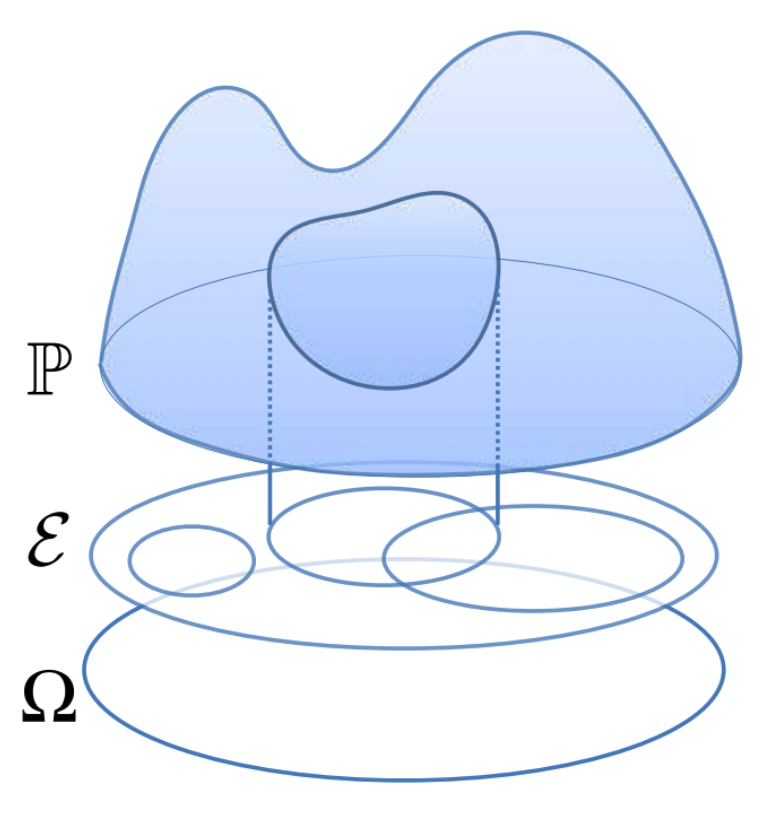	$$\begin{aligned}&\Omega: \text{Set, Samplemspace}\\&E: \text{Events,}\sigma\text{-algebra}\\&P: \text{Probability measure}\end{aligned}$$

Sample Space

• The sets of elementary events.ex.)
  • The number of eyes on the dice.
  • All possible genomes.
  • All possible gene expression profiles
• \(\omega_i\in\Omega\) is the identifier of possible individual stochastic phenomena.

\(\sigma\)-algebra

• The sets of Events.
• Each event \(E_i\subseteq\Omega\)
• Include Empty set \(\varnothing\), universal set \(\Omega\)
• Closure to variable "Set Operation". (ex. Union, intersection, complement)

example)

discrete set	Real set
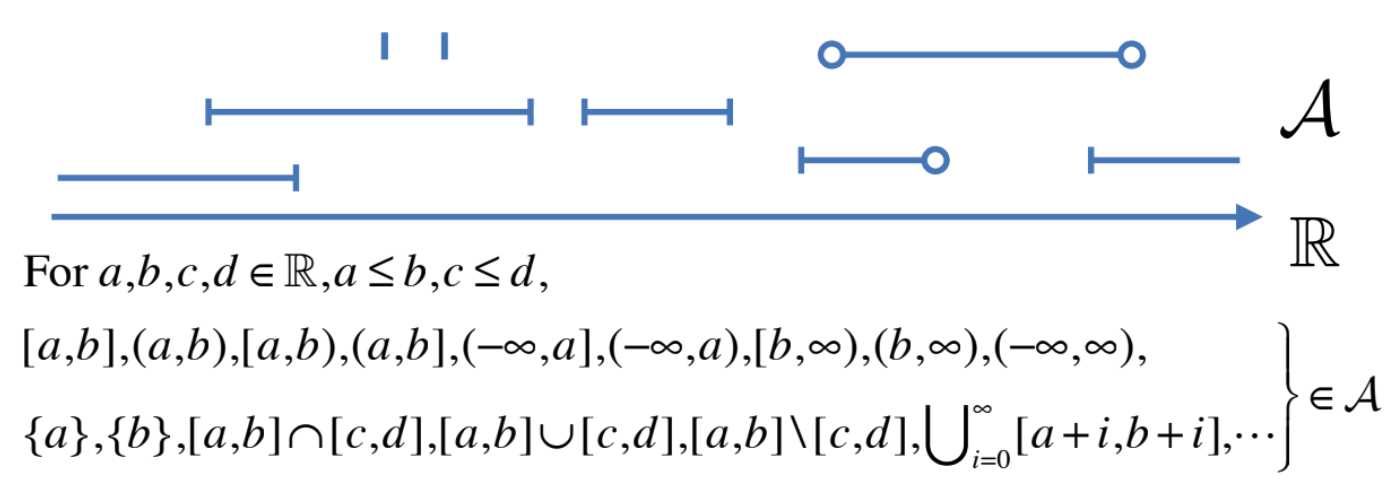Power set	Borel set \(\mathcal{A}\)

Probability measure

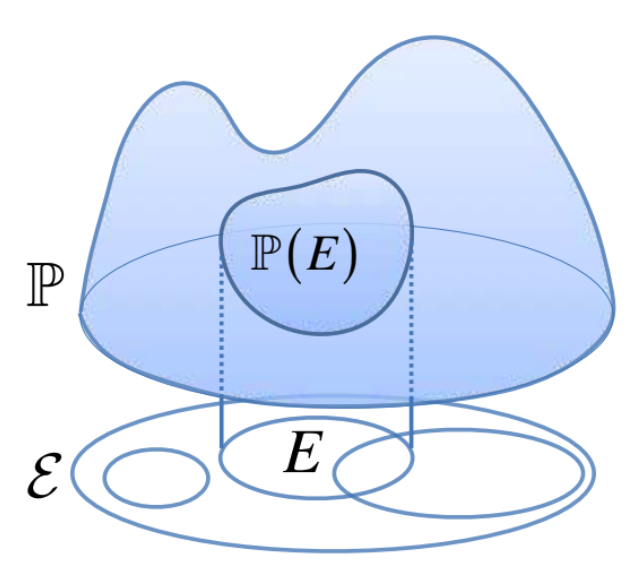$$\begin{aligned}&\mathbb{P} : \mathcal{E} \rightarrow \mathbb{R} \\& 0 \leq \mathbb{P}(E) \leq 1, E \in \mathcal{E} \\&\mathbb{P}(\Omega)=1, \mathbb{P}(\varnothing)=0 \\&\text { For } E_{1}, E_{2}, \cdots \in \mathcal{E}, \text{ s.t. } E_{i} \cap E_{j}=\varnothing, \forall i \neq j \\&\mathbb{P}\left(\bigcup_{i=1}^{\infty} E_{i}\right)=\sum_{i=1}^{\infty} \mathbb{P}\left(E_{i}\right)\end{aligned}$$

Each event is assigned a value that indicates the likelihood or probability of occurrence.

Random variable

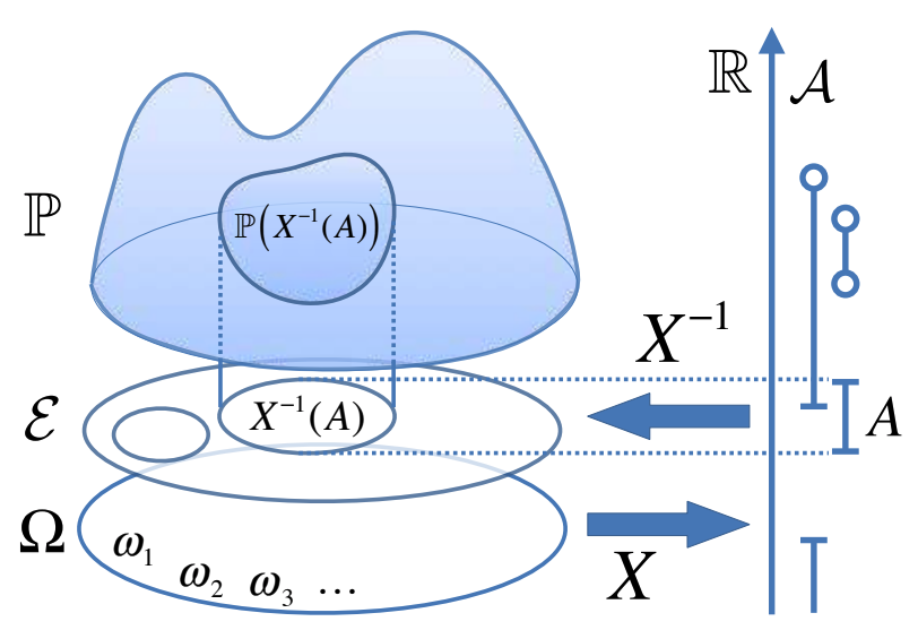	$$\begin{aligned}X: &\text{random variable}\\\Leftrightarrow &X : \Omega \rightarrow \mathbb{R} \\ &\text { s.t. } X^{-1}(A) \in \mathcal{E}, \forall A \in \mathcal{A} \\&X^{-1}(A) :=\{\omega \in \Omega \mid X(\omega) \in A\}\end{aligned}$$

Section1.3 PROBABILITY TERMS AND PROPERTIES

• Probability distribution function \(F_x\) (cumulative distribution)
• Probability density function \(f_x\)
  $$F_x\left(x+dx\right)-F_x\left(x\right)=:f_x(x)dx$$
• Conditional Probability
• Joint Probability distribution
  $$(X,Y): \Omega\rightarrow\mathbb{R}^2; (X,Y)(\omega) = \left(X(\omega),Y(\omega)\right)\\\left(X,Y\right)^{-1}(A) = \left\{\omega\in\Omega|\left(X(\omega),Y(\omega)\right)\in A\right\}$$
• Independent random variables
• Expected Value
• Variance
• Covariance:
  $$\begin{cases}X,Y: \text{independent random variables}\Rightarrow \mathrm{Cov}(X,Y) = 0\\X,Y: \text{independent random variables}\not\Leftarrow \mathrm{Cov}(X,Y) = 0 \end{cases}$$
• Indicator Function:
  $$\mathbb{I}_A(x)=\begin{cases}1 & x\in A\\0 & x\notin A\end{cases},A\in\mathcal{A}$$
• Marginalization

Section1.4 PROBABILITY DISTRIBUTIONS

Look Here!!