色を定量的に表す体系を¬表色系(color specification system)¬と呼ぶ。
表色系 には、人間が知覚した色を記号や色票などで 定性的 に扱う¬顕色系(color appearance system)¬と、実験に基づいて色を心理物理量として 定量的 に扱う¬混色系(color mixing system)¬がある。
色空間
- ¬加法混色(additive colour mixing)¬と¬減法混色(subtractive colour mixing)¬。
- 表色系:
- RGB(CIE-RGB)
- CIE-XYZ表色系
- CIE-L*a*b*
- HSV(HSI)表色系
- マンセル表色系
- YCbCr
加法混色と減法混色
波長が約 400~800nm の¬電磁波(electromagnetic wave)¬を人間の眼に入力すると、電磁波の波長によって定まる色 の光として知覚する。したがって、ある色の光を作る際には、その色に対応する波長の電磁波を用意すれば良いことになる。
しかし、互いに独立した3つの色の光(¬原刺激(reference color stimuli)¬)を混ぜることでも、任意の色を再現できるという経験則が知られている。これは、人間の眼の波長に対する感度の異なる3種類の¬錐体¬の存在で説明できると考えられている。
ここで、複数の色の光を混ぜ合わせることで別の色の光をつくることを¬混色(colour mixing)¬と呼ぶが、これには以下の2つの方法がある。
| # | 加法混色(additive colour mixing) | 減法混色(subtractive colour mixing) |
|---|---|---|
| 画像 | 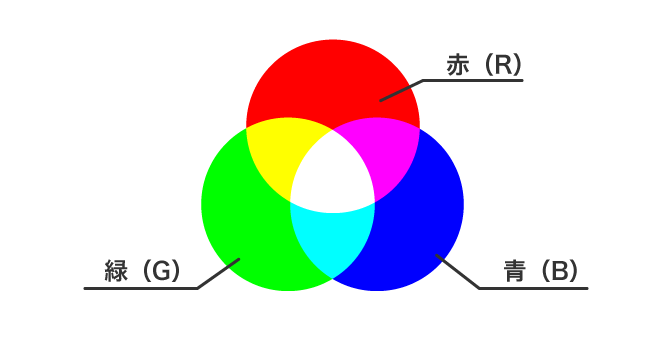 |
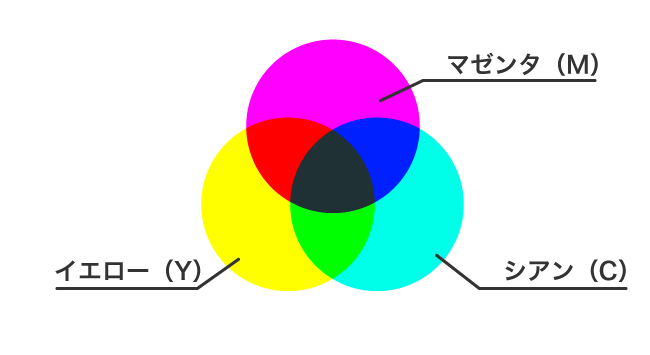 |
| 混色方法 | 白いスクリーン上に異なる色の光を重ねて投影する。 | 白い紙の上で絵の具を混ぜ合わせる。または、色付きフィルタを通して白色光を見る。 |
| 原色 | 赤(red)・緑(green)・青(blue) | シアン(cyan)・マゼンタ(magenta)・黄(yellow) |
表色系
撮影対象の色を測定する際に、3種類の原刺激を用意して 加法混色 し、色が一致した際に両者は¬等色(color match)¬したという。
測定対象からの反射光 \(\mathbf{C}\) は一般に¬連続した分光強度分布を持つ¬が、右辺の3種類の原色光の混色と区別できない。
この方法で対象の光 \(\mathbf{C}\) を表現するとき、三刺激値を調整する前に、原刺激それ自体の大きさを決める必要がある。これは、白色光 \(\mathbf{W}\)(これを¬基礎刺激¬と呼ぶ)に等色するような原刺激の強度を求め、それを単位量とすることで達成されるが、波長 \(\lambda\) に依存する。よって、単位放射量を発行する仮装光 \(\mathbf{U}(\lambda)\)(等エネルギー白色光)を用いて、
の式が成り立つ三値刺激の分布(\(\bar{r}(\lambda), \bar{g}(\lambda), \bar{b}(\lambda)\))を考える。なお、これらを用いれば、先ほどの反射光 \(\mathbf{C}\) の分光エネルギー分布 \(L(\lambda)\) から、次のように三値刺激(\(R,G,B\))を計算できる。
ただし、積分範囲 \(V\) は可視光の波長範囲を表す。この \(\bar{r}(\lambda), \bar{g}(\lambda), \bar{b}(\lambda)\) を¬等色関数(color matching function)¬と呼ぶ。つまり、
- 原刺激 \(\mathbf{R},\mathbf{G},\mathbf{B}\)
- 基礎刺激 \(\mathbf{W}\) に等色する原刺激の強度
- 原刺激に対応した等色関数 \(\bar{r}(\lambda), \bar{g}(\lambda), \bar{b}(\lambda)\)
がわかれば、任意の分光強度分布を持つ光の色彩を3つの数値で表すことができる。
CIE-RGB

原刺激を(R:700.0nm, G:546.1nm, B:435.8nm)として上記の等色関数を用いたもの。等色関数には一部に負の値の領域があるが、この領域では、左辺の反射光 \(\mathbf{C}\) に一定量の原刺激を加えることで等色させる。
CIE-XYZ

CIE-XYZ 表色系は、CIE-RGB 表式系と同時に採用された標準表色系である。CIE-RGB 表色系の等色関数は、部分的に負の値があり、扱いにくかったので、¬等色関数が非負となる¬ように仮想的な原刺激を設定し、¬CIE-RGB表式系の等色関数から線形変換によって¬求めた等色関数 \(\bar{x}(\lambda),\bar{y}(\lambda),\bar{z}(\lambda)\) を用いて三値刺激 \(X,Y,Z\) を求めて色を定量的に表現する。
ここで、明るさを無視する と、任意の色は¬色度座標(trichromatic coodinates)¬で表現できる。さらに、\(X+Y+Z=1\) の制約を用いてこれを平面表示することも可能である。

上図の \(xy\) 色度図中で釣鐘状の曲線を¬スペクトル軌跡(spectrum locus)¬と呼び、軌跡に沿って最も純度の高い単色光が並ぶ。人間が知覚できる全ての色は、380~780nmの点に至るスペクトル軌跡と、その両端を結ぶ直線(¬純紫軌跡(purple lines)¬)で囲まれた領域内にある。