- 講師:本多 淳也
- 参考書:エージェントアプローチ人工知能 第2版
- 参考書:イラストで学ぶ 人工知能概論
講義概要
状態空間
- ありうる局面の1つ1つを状態と言う。
- 状態全体からなる集合を状態空間と言う。
- 目的:初期状態から出発して、許される状態遷移を繰り返し、最終状態へたどり着くこと。
- これは、グラフ(graph)の探索(search)問題と等価(ノードが状態に、エッジが状態遷移にそれぞれ対応する。)
15パズル
- ルール:
- 一度に動かせるのは1パネルのみ。
- 飽きますに隣のパネルをずらす操作のみ可能
- 目標:
- 「できるだけ少ない手数で」与えられた配置から元の配置に戻すこと。
- 元に戻すことが不可能な問題を識別する。
迷路
- 目的:スタートからゴールまで誘導する。
- 状態(state) $s$:移動できる場所
- 行動(action) $a$:進む方向
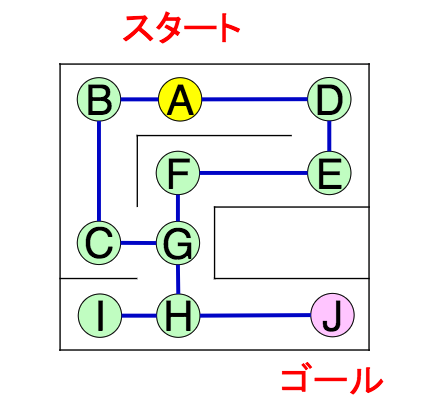
コスト無しグラフの探索
| 用語 | 意味 |
|---|---|
| オープンリスト(open list) | これから探索するノードの候補リスト |
| クローズドリスト(closed list) | 探索が終わったノードのリスト |
| キュー(queue) | 先入れ先出し |
| スタック(stack) | 後入れ先出し |
探索の基本アルゴリズム¶
open_list = [initial_state] # オープンリストは初期化状態のみ
closed_list = [] # クローズドリストは空
while(open_list): # オープンリストが空になるまで以下を繰り返す。
state = getOptimalState(open_list) # オープンリストから(何らかの基準で)状態sを取り出す。
closed_list.append(state) # sをクローズドリストに追加する。
if state==last_state: break # sが最終状態ならば探索終了
open_list += [s for s in state.transibles() if s not in closed_list] # sから遷移可能でまだクローズドリストに入っていない状態をオープンリストに追加する。
深さ優先探索¶
行き止まりに当たるまで進み、ゴールが見つからなかったら直近の分岐に戻って別の道を探す探索法。
- メモリ使用量が少ない
- ゴールが近くにあっても、他の深い別れ道に迷い込むと時間がかかる
- ゴールが複数ある時、一番近くのものが見つかるとは限らない
オープンリストはスタック(後入れ先出し)にする。
open_list = [initial_state]
closed_list = []
while(open_list):
state = open_list.pop(0) # オープンリストの先頭の状態sを取り出す。
closed_list.append(state)
if state==last_state: break
open_list.push([s for s in state.transibles() if s not in closed_list]) # sから遷移可能でまだクローズドリストに入っていない状態をオープンリストの"先頭に"追加する。
幅優先探索¶
分かれ道に来たらそれぞれの道を一歩ずつ進み,ゴールが見つからなかったらそれぞれの道をもう一歩ずつ進む探索法。
- ゴールが近くにある時、早く見つかる。
- ゴールが複数ある時、一番近くのものが見つかる。
- 分かれ道での分岐数が多いとメモリ使用量が多い。
オープンリストはキュー(先入れ後出し)にする。
open_list = [initial_state]
closed_list = []
while(open_list):
state = open_list.pop(-1) # オープンリストの"末尾"の状態sを取り出す。
closed_list.append(state)
if state==last_state: break
open_list.push([s for s in state.transibles() if s not in closed_list]) # sから遷移可能でまだクローズドリストに入っていない状態をオープンリストの"先頭に"追加する。
反復深化探索¶
深さに制限をつけて深さ優先探索を行い、徐々に深さを深くしていく探索法
- ゴールが近くにある時、早く見つかる
- ゴールが複数ある時、一番近くのものが見つかる
- 同じノードを何度も訪れる(分岐が多いと影響小)
まとめ¶
深さ優先探索・幅優先探索・反復深化探索は、グラフに関する特別な知識を使わずにオープンリストから状態を選択することから、ブラインド探索(blined search)と呼ばれる。
| # | 探さ優先探索 | 幅優先探索 | 反復深化探索 |
|---|---|---|---|
| 完全性(必ず解が見つかるか) (completeness) |
$m$ が有限なら Yes | Yes | Yes |
| 時間計算量 (time complexity) |
$\mathrm{O}(b^m)$ | $\mathrm{O}(b^d)$ | $\mathrm{O}(b^d)$ |
| 空間計算量(space complexity) | $\mathrm{O}(bm)$ | $\mathrm{O}(b^d)$ | $\mathrm{O}(bd)$ |
| 最適性(一番近くの解が見つかるか) |
Yes | Yes | Yes |
- $b$:最大分岐数
- $d$:一番浅い解の深さ
- $m$:最大の深さ
コスト付きグラフの探索
各エッジに遷移コストが割り当てられている場合の最適遷移パス探索問題。
- ブラインド探索:グラフに関する特別な知識を使わずにオープンリストから状態を選択。
- 貪欲探索(greedy search):現在の状態からの遷移コストが最小の状態を選ぶ。(深さ優先探索に対応)
- 最適探索(optimal search):初期状態からの遷移コスト和が最小の状態を選ぶ。(各コストが1だと幅優先探索になる。ダイクストラ法とも。)
- ヒューリスティック探索(最良優先探索, best-first search):グラフに関する何らかの知識を使ってオープンリストから適切と思われる状態を選択。
- 貪欲最良優先探索
- $A^{\ast}$ 探索
貪欲最良優先探索¶
- $\hat{h}(s)$ を最小にする状態を選ぶ
- $h(s)$:$s$ から最終状態までの遷移コスト和の最小値
- $\hat{h}(s)$:$h(s)$ の推定(ヒューリスティック関数)
- 一度オープンリストに入ったの評価値更新は不要
- ヒューリスティック関数の選び方:
- ユーザが事前知識により構築(例:直線距離)
- データから機械学習により自動構築
- 一般には完全性も最適性もないが、実用上は(そこそこ)うまくいくことが(それなりに)多い。
$A^{\ast}$ 探索(A-start search)¶
- $s$ を経由する場合の遷移コスト和の推定値 $\left(\hat{g}(s)+\hat{h}(s)\right)$ を最小にする状態を選ぶ。
- $g(s)$:初期状態から $s$ までの遷移コスト和の最小値
- $\hat{g}(s)$:探索済みノードから $s$ に遷移する場合の最小値(ダイクストラ法と同じ)
- ノード $s$ を訪れると隣接ノードの $\hat{g}(s^{\prime})$ が更新される。
- $h(s)$:$s$ から最終状態までの遷移コスト和の最小値
- $\hat{h}(s)$:$h(s)$ のヒューリスティック推定値
- 最適経路上の $s$ ではいずれも $g(s)+h(s)$ が最小、経路外の点ではそれより大きい値をとることを利用
- $\forall s, 0\leq\hat{h}(s)\leq h(s)$ が成り立つ時、$\hat{h}(s)$ は許容的(admissible)であるといい、この場合には $A^{\ast}$ 探索は最適性を持つ。
※ 実装等は、レポート課題に記載。
In [1]:
from kerasy.search.Astar import OptimalTransit
In [2]:
n=3
m=3
initial_str = "2,-1,6,1,3,4,7,5,8"
last_str = "1,2,3,4,5,6,7,8,-1"
In [3]:
OptimalTransit(n,m,initial_str,last_str,heuristic_method="Manhattan_distance",n_row=5)
ゲーム木の探索
2人のプレイヤーが交互に遷移先を決めるゲーム(ex. 将棋・囲碁・リバーシ・◯×など)における最適遷移探索問題
- ミニマックス探索
- 自分は一番良い(点数を最大化する)手を選ぶ
- 相手は一番悪い(点数を最小化する)手を選ぶ
- アルファ・ベータ探索
- ミニ・マックス探索では、全ての局面に対する点数を求める必要があり、時間がかかる。
- 不要な点数計算を省略することで効率化
- $\alpha$:max計算の際の下界値
- $\beta$:min計算の際の上界値
- モンテカルロ木探索
- アルファ・ベータ法を用いても、ゲーム木を深く探索するのは困難($b^d$ が $b^{d/2}$ になる程度。)
- そこで、ランダムに手を打つ。
- 囲碁やスケジューリングなどで活用されている。
まとめ
- 広大な状態空間を効率よく探索したい
- コスト無しグラフの探索
- コスト付きグラフの探索
- ゲーム木の探索
- 膨大な状態空間の探索には,近似的な手法が有用
- 事前知識や機械学習によるヒューリスティック関数の構築
- モンテカル
- 木探索
In [ ]: