import numpy as np
import matplotlib.pyplot as plt
Section4.1 Expectation Maximization Algorithm¶
- The expectation maximization algorithm, or EM algorithm, is a general technique for finding maximum likelihood solutions for probabilistic models having latent variable.
- Consider a probabilistic model in which we collectively denote
- all of the observed variables by $\mathbf{X}$
- all of the hidden variables by $\mathbf{Z}$ (assuming discrete, but discussion is identical if continuous)
- joint distribution by $p\left(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}\right)$
- Goal is to maximize the likelihood function that is given by $$p\left(\mathbf{X}|\boldsymbol{\theta}\right) = \sum_{\mathbf{Z}}p\left(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}\right)\qquad (9.69)$$
Properties¶
- Guaranteed to terminate
- Likelihood always increases
- Solving M-step is often easy
- No need to traverse the data
- Separation of parameter dependency
- $\log(pq)=\log(p)+\log(q)$
- Sometimes solved exactly
- Often a few times faster than gradient descent (if stopping condition is not too stringent)
- Expectation values characterize the optimized model
Lower Bound of Likelihood¶
$\mathcal{L}\left(q,\boldsymbol{\theta}\right)$ and $\mathrm{KL}\left(q\|p\right)$¶
- We shall suppose that
- direct optimization of $p(\mathbf{X}|\boldsymbol{\theta})$ is difficult
- the optimization of the complete-data likelihood function $p\left(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}\right)$ is significantly easier
- We introduce a distribution $q\left(\mathbf{Z}\right)$ defined over the latent variables.
- For any choice of $q\left(\mathbf{Z}\right)$, the following decomposition holds $$ \begin{aligned} \ln p\left(\mathbf{X}|\boldsymbol{\theta}\right) &= \mathcal{L}\left(q,\boldsymbol{\theta}\right) + \mathrm{KL}\left(q\|p\right) &(9.70)\\ \mathcal{L}\left(q,\boldsymbol{\theta}\right) &= \sum_{\mathbf{Z}}q(\mathbf{Z})\ln\left\{\frac{p\left(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}\right)}{q(\mathbf{Z})}\right\} & (9.71)\\ \mathrm{KL}\left(q\|p\right) &= -\sum_{\mathbf{Z}}q(\mathbf{Z})\ln\left\{\frac{p\left(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}\right)}{q(\mathbf{Z})}\right\} & (9.72) \end{aligned} $$
- NOTE: $\mathcal{L}(q,\boldsymbol{\theta})$ is a functional of the distribution $q(\mathbf{Z})$, and a function of the parameters $\boldsymbol{\theta}$
$$ \begin{aligned} \mathcal{L}\left(q,\boldsymbol{\theta}\right) + \mathrm{KL}\left(q\|p\right) &=\sum_{\mathbf{Z}}q(\mathbf{Z})\ln\left\{\frac{p\left(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}\right)}{q(\mathbf{Z})}\right\} -\sum_{\mathbf{Z}}q(\mathbf{Z})\ln\left\{\frac{p\left(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}\right)}{q(\mathbf{Z})}\right\}\\ &= \sum_{\mathbf{Z}}q(\mathbf{Z})\ln\left\{\frac{p\left(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}\right)}{p\left(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}\right)}\right\}\\ &= \sum_{\mathbf{Z}}q(\mathbf{Z})\ln p\left(\mathbf{X}|\boldsymbol{\theta}\right)\\ &= \ln p\left(\mathbf{X}|\boldsymbol{\theta}\right) \end{aligned}$$
- From $(9.72)$, we see that $\mathrm{KL}(q\|p)$ is the Kullback-Leibler divergence between $q(\mathbf{Z})$ and the posterior distribution $p(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta})$
- Kullback-Leibler divergence satisfies $\mathrm{KL}(q\|p)\geq0$ with eqyality if, and only if, $q(\mathbf{Z})=p(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta})$.
- Therefore, $\mathcal{L}(q,\boldsymbol{\theta})\leq\ln p(\mathbf{X}|\boldsymbol{\theta})$, in other words that $\mathcal{L}(q,\boldsymbol{\theta})$ is a lower bound on $\ln p(\mathbf{X}|\boldsymbol{\theta})$
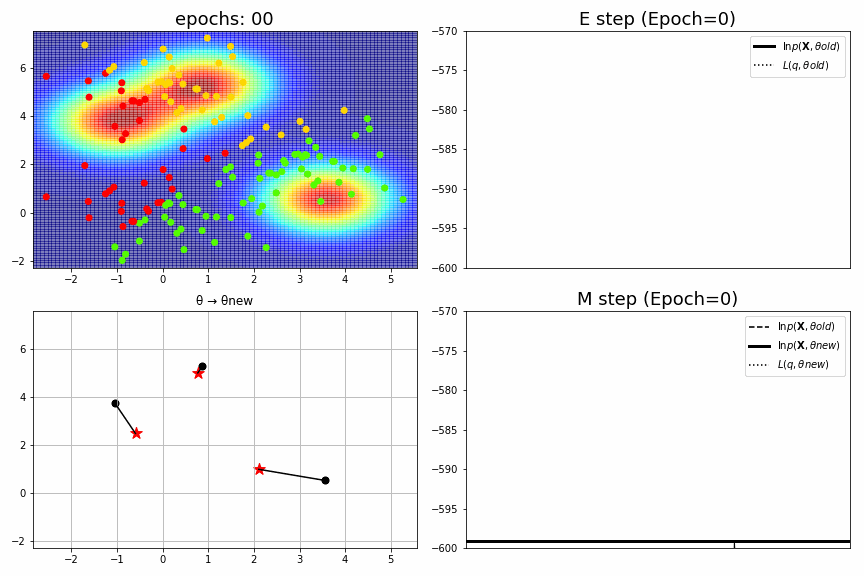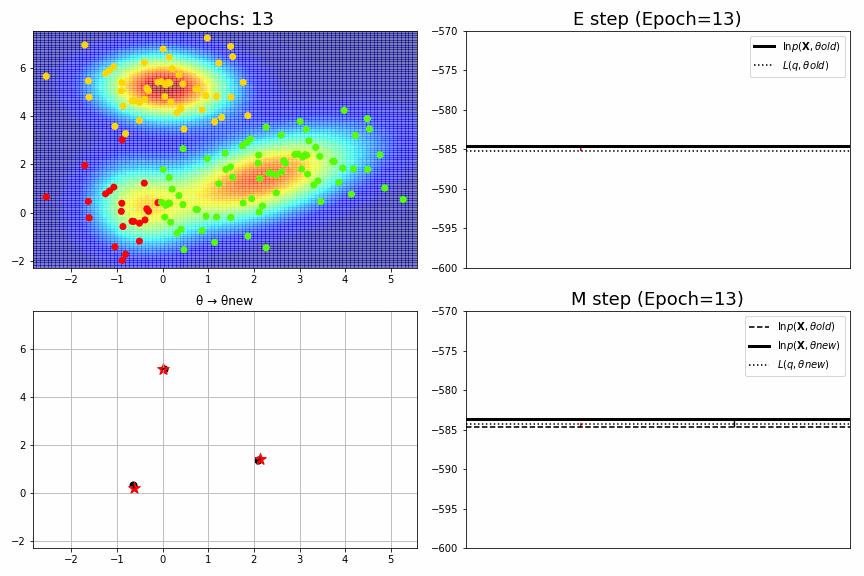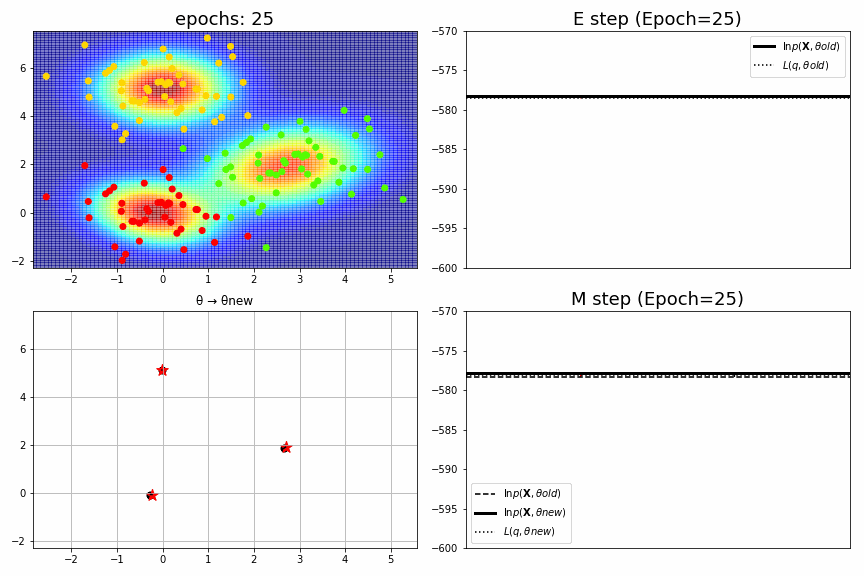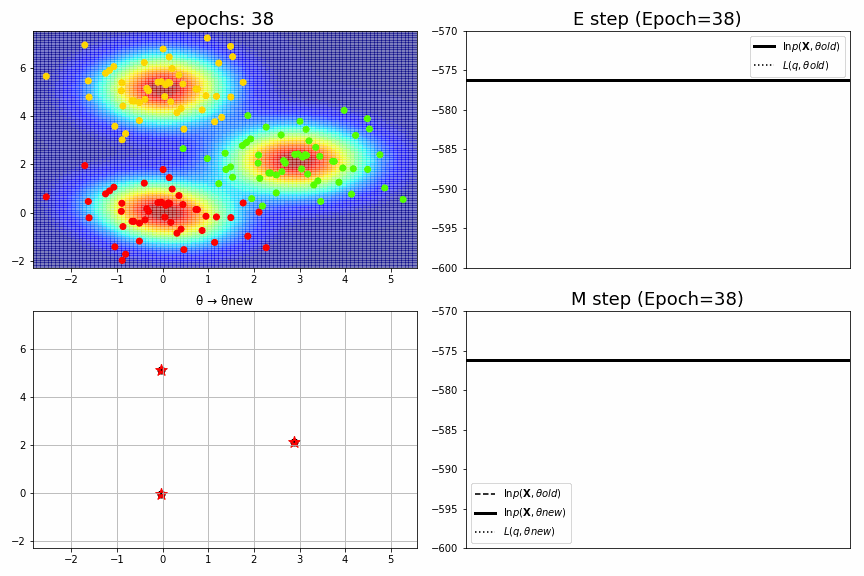
E step¶
In the E step, the lower bound $\mathcal{L}(q,\boldsymbol{\theta}^{\text{old}})$ is maximized with respect to $q(\mathbf{Z})$ while holding $\boldsymbol{\theta}^{\text{old}}$ fixed.
- $\ln p(\mathbf{X}|\boldsymbol{\theta}^{\text{old}})$ does not depend on $q(\mathbf{Z})$
- the largest value of $\mathcal{L}(q,\boldsymbol{\theta}^{\text{old}})$ will occur when the Kullback-Leibler divergence vanishes.
∴ When $q(\mathbf{Z})$ is equal to the posterior distribution $p(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{\text{old}})$, $\mathrm{KL}(q\|p)=0$ and the lower bound $\mathcal{L}(q,\boldsymbol{\theta}^{\text{old}})$ will be maximized.
M step¶
In the M step, the lower bound $\mathcal{L}(q,\boldsymbol{\theta}^{\text{old}})$ is maximized with respect to $\boldsymbol{\theta}$ to give some new value $\boldsymbol{\theta}^{\text{new}}$ while holding $q(\mathbf{Z})$ fixed.
- This will cause the lower bound $\mathcal{L}$ to increase
- This will necessarily cause the corrresponding log likelihood function to increase.
- Because $q$ is held fixed during the M step, it will not equal the new posterior distribution $p(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{\text{old}})$ $\left(\mathrm{KL}(q\|p)\neq0\right)$
$\mathcal{Q}(\boldsymbol{\theta},\boldsymbol{\theta}^{\text{old}})$¶
If we substitute $q(\mathbf{Z}) = p\left(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{\text{old}}\right)$ into $(9.71)$,
$$ \begin{aligned} \mathcal{L}\left(q,\boldsymbol{\theta}\right) &= \sum_{\mathbf{Z}}q(\mathbf{Z})\ln\left\{\frac{p\left(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}\right)}{q(\mathbf{Z})}\right\} & (9.71)\\ &= \sum_{\mathbf{Z}}p\left(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{\text{old}}\right)\ln p\left(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}\right) - \sum_{\mathbf{Z}}p\left(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{\text{old}}\right)\ln p\left(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{\text{old}}\right)\\ &= \mathcal{Q}\left(\boldsymbol{\theta},\boldsymbol{\theta}^{\text{old}}\right) + \text{const.} \end{aligned} $$∴ "Maximizing $\mathcal{L}(q,\boldsymbol{\theta})$" is equal to "Maximizing $\mathcal{Q}\left(\boldsymbol{\theta},\boldsymbol{\theta}^{\text{old}}\right)$".
from kerasy.ML.MixedDistribution import MixedGaussian
# Train Data.
data = np.concatenate([
np.random.RandomState(0).multivariate_normal(mean=[0, 0], cov=np.eye(2), size=50),
np.random.RandomState(0).multivariate_normal(mean=[0, 5], cov=np.eye(2), size=50),
np.random.RandomState(0).multivariate_normal(mean=[3, 2], cov=np.eye(2), size=50),
])
X,Y = data.T
K = 3
# Back Ground Color
xmin,ymin = np.min(data, axis=0)-0.3
xmax,ymax = np.max(data, axis=0)+0.3
Xs,Ys = np.meshgrid(np.linspace(xmin, xmax, 100), np.linspace(ymin, ymax, 100))
XYs = np.c_[Xs.ravel(),Ys.ravel()]
model = MixedGaussian(K=3, random_state=1234)
model.fit(data, memo_span=1)
ll_hist = [ll for _,_,_,ll in model.history]
mu_hist = [mu for _,_,(mu,_,_),_ in model.history]
plt_model = MixedGaussian(K=3)
plt_model.N, plt_model.M = data.shape
L_old = min(ll_hist)-300
for epoch,idx,(mu,S,pi),ll in model.history[:-1]:
fig = plt.figure(figsize=(12,8))
ll_old = ll_hist[epoch]; ll_new = ll_hist[epoch+1]
mu_old = mu_hist[epoch]; mu_new = mu_hist[epoch+1]
L_new = np.random.uniform(low=0.3,high=0.5)*(ll_new-ll_old)+ll_old # 真面目に計算していない。
dL_old=ll_old-L_old; dL_new=L_new-ll_old; dll_old=ll_new-ll_old
ax1 = fig.add_subplot(2,2,1)
plt_model.mu = mu; plt_model.S = S; plt_model.pi = pi
gammas = plt_model.predict(XYs)
Zs = np.sum(gammas, axis=1).reshape(Xs.shape) # Likelihood.
ax1.pcolor(Xs, Ys, Zs, alpha=.5,cmap="jet")
ax1.scatter(X,Y,c=idx, cmap="prism")
ax1.set_xlim(xmin, xmax), ax1.set_ylim(ymin, ymax), ax1.set_title(f"epochs: {epoch:>02}", fontsize=18)
ax2 = fig.add_subplot(2,2,2)
ax2.axhline(ll_old, color="black", label="$\ln p(\mathbf{X},θold)$", linewidth=3)
ax2.axhline(L_old, color="black", label="$L(q,θold)$", linestyle=":")
ax2.arrow(x=0.3, y=L_old, dx=0, dy=dL_old, head_width=dL_old/6000, head_length=dL_old*0.1, fc='red', ec='red', length_includes_head=True)
ax2.set_title(f"E step (Epoch={epoch})", fontsize=18), ax2.legend(), ax2.set_xticks([]), ax2.set_ylim(-600, -570)
ax3 = fig.add_subplot(2,2,3)
for k in range(K):
xb,yb = mu_old[k]; xa,ya = mu_new[k]
ax3.plot((xb,xa),(yb,ya), color="black")
ax3.scatter(xb,yb, color="black", s=50)
ax3.scatter(xa,ya, color="red", marker="*", s=150)
ax3.set_xlim(xmin, xmax), ax3.set_ylim(ymin, ymax), ax3.set_title("θ → θnew")
ax3.grid()
ax4 = fig.add_subplot(2,2,4)
L_new = np.random.uniform(low=0.3,high=0.5)*(ll_new-ll_old)+ll_old # 真面目に計算していない。
ax4.axhline(ll_old, color="black", label="$\ln p(\mathbf{X},θold)$", linestyle="--")
ax4.axhline(ll_new, color="black", label="$\ln p(\mathbf{X},θnew)$", linewidth=3)
ax4.axhline(L_new, color="black", label="$L(q,θnew)$", linestyle=":")
ax4.arrow(x=0.7, y=ll_old, dx=0, dy=dll_old, head_width=dll_old/6000, head_length=dll_old*0.1, fc='k', ec='k', length_includes_head=True)
ax4.arrow(x=0.3, y=ll_old, dx=0, dy=dL_new, head_width=dL_new/6000, head_length=dL_new*0.1, fc='red', ec='red',length_includes_head=True)
ax4.set_title(f"M step (Epoch={epoch})", fontsize=18), ax4.legend(), ax4.set_xticks([]), ax4.set_ylim(-600, -570)
plt.tight_layout()
plt.savefig(f"img/img{epoch:>02}")
L_old = L_new
fig_no=0
L_old = min(ll_hist)-300
for epoch in range(len(model.history)-1):
ll_old = ll_hist[epoch]; ll_new = ll_hist[epoch+1]
L_new = np.random.uniform(low=0.3,high=0.5)*(ll_new-ll_old)+ll_old # 真面目に計算していない。
dL_old=ll_old-L_old; dL_new=L_new-ll_old; dll_old=ll_new-ll_old
# Estep
fig = plt.figure(figsize=(3,10))
ax = fig.add_subplot(1,1,1)
ax.axhline(ll_old, color="black", label="$\ln p(\mathbf{X},θold)$", linewidth=3)
ax.axhline(L_old, color="black", label="$L(q,θold)$", linestyle=":")
ax.arrow(x=0.3, y=L_old, dx=0, dy=dL_old, head_width=dL_old/60, head_length=dL_old*2e-1, fc='red', ec='red', length_includes_head=True)
ax.set_title(f"E step (Epoch={epoch})", fontsize=18), ax.legend(), ax.set_xticks([]), ax.set_ylim(-600, -570)
plt.savefig(f"img/img{fig_no:>02}"); fig_no+=1
plt.clf()
# Mstep
fig = plt.figure(figsize=(3,10))
ax = fig.add_subplot(1,1,1)
L_new = np.random.uniform(low=0.3,high=0.5)*(ll_new-ll_old)+ll_old # 真面目に計算していない。
ax.axhline(ll_old, color="black", label="$\ln p(\mathbf{X},θold)$", linestyle="--")
ax.axhline(ll_new, color="black", label="$\ln p(\mathbf{X},θnew)$", linewidth=3)
ax.axhline(L_new, color="black", label="$L(q,θnew)$", linestyle=":")
ax.arrow(x=0.7, y=ll_old, dx=0, dy=dll_old, head_width=dll_old/60, head_length=dll_old*2e-1, fc='k', ec='k', length_includes_head=True)
ax.arrow(x=0.3, y=ll_old, dx=0, dy=dL_new, head_width=dL_new/60, head_length=dL_new*2e-1, fc='red', ec='red',length_includes_head=True)
ax.set_title(f"M step (Epoch={epoch})", fontsize=18), ax.legend(), ax.set_xticks([]), ax.set_ylim(-600, -570)
plt.savefig(f"img/img{fig_no:>02}");fig_no+=1
plt.clf()
L_old = L_new

Section4.2 Mixture Model¶
Implementation¶
Section4.3 Linear Regression¶
Least Squares¶
polynomial function¶
we observe a real-value input variable $x$ and we wish to use this observation to predict the value of a real-valued target variable $t$. In the most simplest approach based on curve fitting, we shall fit the data using a polynomial function of the form : $$y(x,\mathbf{w}) = w_0+w_1x+w_2x^2+\cdots+w_Mx^M=\sum_{j=0}^Mw_jx^j\qquad (1.1)$$
data¶
we are given
- a training set comprising $N$ observation of $x$, written $\mathbf{X}\equiv(\mathbf{x_1},\ldots,\mathbf{x}_N)^T$
- with corresponding observation of the values of $t$, denoted $\mathbf{t}\equiv(t_1\ldots,t_N)^T$
we can difine $M$, which is the order of the polynomial.
- The values of the coefficients($w_j$) will be determined by fitting the polynomial to the training data.
- This can be done by minimizing an error function that measures the misfit between the function $y(x,\mathbf{w})$ and the training set data points.
- One simple choice of error function, which is widely used, is given by the sum of the squares of the errors $$E(\mathbf{w}) = \frac{1}{2}\mathrm{RSS} = \frac{1}{2}\sum_{n=1}^N\left\{y(\mathbf{x}_n,\mathbf{w}) - t_n\right\}^2\qquad (1.2)$$
- (the factor of $1/2$ is included for later convenience.)
Trainig¶
- Aim: find the best $\mathbf{w}^{\star}=\underset{w\in\mathbb{R}}{\mathrm{argmin}}\left\{\mathrm{RSS}(\mathbf{w})\right\}$
- $\mathbf{t} = \left(\begin{matrix}t_1\\\vdots\\t_N\end{matrix}\right),\quad\mathbf{X} = \left(\begin{matrix}x_1^0&x_1^1&\cdots&x_1^M\\x_2^0&x_2^1&\cdots&x_2^M\\\vdots&\vdots&\ddots&\vdots\\x_N^0&x_N^1&\cdots&x_N^M\end{matrix}\right),\quad\mathbf{w}=\left(\begin{matrix}w_1\\\vdots\\w_M\end{matrix}\right)$
- $\mathrm{RSS}(\mathbf{w}) = \left(\mathbf{t} - \mathbf{Xw}\right)^T\left(\mathbf{t} - \mathbf{Xw}\right)$
- Solution: $$ \begin{aligned} \frac{\partial E(\mathbf{w})}{\partial\mathbf{w}} &=\frac{1}{2}\frac{\partial}{\partial\mathbf{w}}\|\mathbf{t}-\mathbf{Xw}\|^2\\ &=\frac{1}{2}\frac{\partial}{\partial\mathbf{w}}\left(\|\mathbf{t}\|^2 - 2\mathbf{w}^T\mathbf{X}^T\mathbf{t} + \|\mathbf{Xw}\|^2\right)\\ &=\frac{1}{2}\frac{\partial}{\partial\mathbf{w}}\left(\|\mathbf{t}\|^2 - 2\mathbf{w}^T\mathbf{X}^T\mathbf{t} + \mathbf{w}^T\mathbf{X}^T\mathbf{Xw}\right)\\ &=\frac{1}{2} \left(-2\mathbf{X}^T\mathbf{t} + \left(\mathbf{X}^T\mathbf{X} + \left(\mathbf{X}^T\mathbf{X}\right)^T\right)\mathbf{w}\right)\\ &= -\mathbf{X}^T\mathbf{t}+\mathbf{X}^T\mathbf{Xw}=\mathbf{0}\\ \therefore\mathbf{w}^{\star} &= \left(\mathbf{X}^T\mathbf{X}\right)^{-1}\mathbf{X}^T\mathbf{t} \end{aligned}$$
※ In the following programs, I use np.linalg.solve to calcurate $\mathbf{w}^{\ast}$
| equation | program |
|---|---|
| $$\left(\mathbf{X}^T\mathbf{X}\right)\mathbf{w}^{\star} = \mathbf{X}^T\mathbf{t}$$ | w = np.linalg.solve(X.T.dot(X), X.T.dot(t)) |
N = 15
Ms = [2,4,8,16]
seed = 0
# Training data.
x = np.random.RandomState(seed).uniform(low=0, high=1, size=N)
Noise = np.random.RandomState(seed).normal(loc=0, scale=0.1, size=N)
t = np.sin(2*np.pi*x) + Noise
fig=plt.figure(figsize=(12,8))
for i,M in enumerate(Ms):
ax=fig.add_subplot(2,2,i+1)
# Training.
X = np.array([x**m for m in range(M+1)]).T
w = np.linalg.solve(X.T.dot(X), X.T.dot(t))
# For Validation plot.
Xs = np.linspace(0,1,1000)
t_true = np.sin(2*np.pi*Xs)
t_pred = w.dot(np.array([Xs**m for m in range(M+1)]))
# RSS(Residual Sum of Squares)
residual = t - w.dot(np.array([x**m for m in range(M+1)]))
RSS = residual.T.dot(residual)
# Plot.
ax.plot(Xs,t_true,color="black", label="$t=\sin(2\pi x)$")
ax.plot(Xs,t_pred,color="red", label=f"prediction ($M={M}$)")
ax.scatter(x,t,edgecolors='blue',facecolor="white",label="train data")
ax.set_title(f"Results (RSS=${RSS:.3f}$,M=${M}$)"), ax.set_xlabel("$x$"), ax.set_ylabel("$t$")
ax.set_xlim(0,1), ax.set_ylim(-1.2,1.2)
ax.legend()
plt.tight_layout()
plt.show()
Regularized Least Square¶
lambda_ = 1e-4
fig=plt.figure(figsize=(12,8))
for i,M in enumerate(Ms):
ax=fig.add_subplot(2,2,i+1)
# Training.
X = np.array([x**m for m in range(M+1)]).T
w = np.linalg.solve(lambda_*np.identity(M+1) + X.T.dot(X), X.T.dot(t))
# For Validation plot.
Xs = np.linspace(0,1,1000)
t_true = np.sin(2*np.pi*Xs)
t_pred = w.dot(np.array([Xs**m for m in range(M+1)]))
# RSS(Residual Sum of Squares)
residual = t - w.dot(np.array([x**m for m in range(M+1)]))
RSS = residual.T.dot(residual)
# Plot.
ax.plot(Xs,t_true,color="black", label="$t=\sin(2\pi x)$")
ax.plot(Xs,t_pred,color="red", label=f"prediction ($M={M}$)")
ax.scatter(x,t,edgecolors='blue',facecolor="white",label="train data")
ax.set_title(f"Results (RSS=${RSS:.3f}$,M=${M}$,$\lambda={lambda_}$)"), ax.set_xlabel("$x$"), ax.set_ylabel("$t$")
ax.set_xlim(0,1), ax.set_ylim(-1.2,1.2)
ax.legend()
plt.tight_layout()
plt.show()
Section4.4 Bayesian Inference¶
Maximal Likelihood Estimate¶
$$ l(\boldsymbol{\theta}|D) = \log L(\boldsymbol{\theta}|D) = \log\mathbb{P}(D|\boldsymbol{\theta})\\ \hat{\boldsymbol{\theta}}_{\text{ML}} = \underset{\boldsymbol{\theta}}{\text{argmax}}l(\boldsymbol{\theta}|D) $$※ $l$: large → High probability of observing $D$ from the model $\boldsymbol{\theta}$
Maximum a Posteriori Estimate¶
- Maximum a posteriori estimate $$ \begin{aligned} \hat{\boldsymbol{\theta}_{\text{MAP}}} &= \underset{\boldsymbol{\theta}}{\text{argmax}}f(\boldsymbol{\theta}|D)\\ &= \underset{\boldsymbol{\theta}}{\text{argmax}}f(D|\boldsymbol{\theta})f(\boldsymbol{\theta})\\ &= \underset{\boldsymbol{\theta}}{\text{argmax}}\left\{l(\boldsymbol{\theta}|D) L \log f(\boldsymbol{\theta})\right\}\\ \end{aligned} $$
- Posterior mean estimate $$ \hat{\boldsymbol{\theta}_{\text{PME}}} = \int\boldsymbol{\theta}f(\boldsymbol{\theta}|D)d\boldsymbol{\theta} $$
Implementation of Gaussian Prior for Regression.¶
seed = 123
from kerasy.ML.linear import BayesianLinearRegression
from kerasy.utils.preprocessing import GaussianBaseTransformer
from kerasy.utils.data_generator import generateSin, generateGausian
N = 25; D = 1; M = 25
xmin=0; xmax=1
alpha = 1
beta = 25
x_test = np.linspace(xmin,xmax,1000)
y_test = np.sin(2*np.pi*x_test)
x_train,y_train = generateSin(size=N, xmin=xmin,xmax=xmax,seed=seed)
_,y_noise = generateGausian(size=N, x=x_train, loc=0, scale=1/beta, seed=seed)
y_train += y_noise
# transform
mu = np.linspace(xmin,xmax,M); sigma = 0.1
phi = GaussianBaseTransformer(mu=mu, sigma=sigma)
x_train_features = phi.transform(x_train)
x_test_features = phi.transform(x_test)
random_idx = np.random.RandomState(seed).choice(N, N)
fig = plt.figure(figsize=(16,8))
for i,n in enumerate([1,2,4,25]):
ax = fig.add_subplot(2,2,i+1)
model = BayesianLinearRegression(alpha=alpha, beta=beta)
model.fit(x_train_features[random_idx[:n]],y_train[random_idx[:n]])
y_pred,y_std = model.predict(x_test_features)
ax.plot(x_test,y_test,color="black", label="$\sin(2\pi x)$")
ax.plot(x_test,y_pred,color="red", label="predict($\mu$)")
ax.fill_between(x_test, y_pred-y_std, y_pred+y_std, color="pink", alpha=0.5)
ax.scatter(x_train[random_idx[:n]],y_train[random_idx[:n]],s=150,edgecolors='black',facecolor="white",label="train data")
ax.set_ylim(-1.5,1.5), ax.legend(), ax.set_title(f"Bayesian Linear Regression (N={n})")
plt.tight_layout()
plt.show()