In [1]:

import numpy as np
import matplotlib.pyplot as plt

Section2.1 Central Limit Theorem¶

Law of Large Numbers¶

Estimation is accurate with many samples.
Foundation of repeated measurement.
Regardless of true distribution.
Assuming independence.

Theorem¶

Let $\mathbf{X}_1,\mathbf{X}_2,\ldots,\mathbf{X}_n$ be an independent trials process, with finite expected value $\mu = \mathbb{E}\left(\mathbf{X}_i\right)$
Let $\bar{\mathbf{X}}_n = \frac{1}{n}\left(\mathbf{X}_1,\mathbf{X}_2+\cdots+\mathbf{X}_n\right)$ be a sample mean.
Weak law: $$\lim_{n\rightarrow\infty}P\left(|\bar{\mathbf{X}}_n-\mu|>\varepsilon\right) = 0 \quad\left(\forall\varepsilon>0\right)$$
Strong law $$P\left(\lim_{n\rightarrow\infty}\bar{\mathbf{X}}_n = \mu\right) = 1$$

Proof.¶

We assume that $\bar{\mathbf{X}}_n$ have the "finite" variance $\sigma^2$

Since $\mathbf{X}_1,\mathbf{X}_2,\ldots,\mathbf{X}_n$ are independent and have the same distributions, we can apply Chebyshev Inequality. We obtain $$0\leq P\left(|\bar{\mathbf{X}}_n - \mu|>\varepsilon\right)\leq\frac{1}{\varepsilon^2}\mathbb{V}(\bar{\mathbf{X}}_n) = \frac{1}{\varepsilon^2}\frac{\sigma^2}{n}\rightarrow0\quad(n\rightarrow\infty)$$

Chebyshev Inequality¶

Let $\mathbf{X}$ be a discrete random variable with expected value $\mu=\mathbb{E}\left(\mathbf{X}\right)$ $$ P \left(|\mathbf{X}-\mu|>\varepsilon\right)\leq\frac{\mathbb{V}\left(\mathbf{X}\right)}{\varepsilon^2}$$

Example¶

In [2]:

N = 1000
seed = 0

In [3]:

trials = np.arange(1,N+1)

In [4]:

dices = np.random.RandomState(seed).randint(low=1, high=6+1, size=N)
ave_dices = np.cumsum(dices)/trials

In [5]:

plt.axhline(3.5, color="blue", label="Theoretical mean")
plt.plot(trials, ave_dices, label="Observed average", color="green")
plt.ylim(1, 6)
plt.title("Average dice roll by number of rolls")
plt.ylabel("Average")
plt.xlabel("Number of trials")
plt.grid()
plt.legend()
plt.show()

If we keep rolling the dice over and over again, the sample average of dice roll will converge to the true average.

Exception¶

The law of large numbers assumes the existance of expected values. Therefore, it will not hold when there is no expected value. (ex. Cauchy distribution)

Cauchy distribution¶

$$ \begin{aligned} f(x;x_0,\gamma) &= \frac{1}{\pi\gamma\left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]} = \frac{1}{\pi}\frac{\gamma}{\left(x-x_0\right)^2 + \gamma^2} & \begin{cases}x_0: \text{Location paramete}\\\gamma: \text{Scale parameter}\end{cases}\\ f(x;0,1) &= \frac{1}{\pi\left(1+x^2\right)} & (\text{standard cauchy distribution}) \end{aligned} $$

In [6]:

N = 5000
K = 3
seed = 1

In [7]:

trials = np.arange(1,N+1)

In [8]:

samples = np.random.RandomState(seed).standard_cauchy(size=(K*N)).reshape((K,N))
ave_samples = np.cumsum(samples, axis=1)/trials

In [9]:

for k in range(K):
    plt.plot(trials, ave_samples[k], label=f"Observation {k+1}")
plt.ylabel("$(\mathbf{X}_1+\cdots+\mathbf{X}_n)/n$")
plt.xlabel("n")
plt.legend()
plt.grid()

Central Limit Theorem¶

Sample mean follows normal distribution.
Foundation of many statistical tests.
Regardless of true distribution.
Assuming independence.

Theorem¶

Let $\{\mathbf{X}_1,\ldots,\mathbf{X}_n\}$ be a random sample of size $n$, which is a sequence of independent and identically distributed random variables drawn from a distribution.
- expected value given by $\mu$.
- finite variance given by $\sigma^2$.
Let $S_n:=\sum_{k=1}^n\mathbf{X}_k$ $$P\left(\frac{S_n-n\mu}{\sqrt{n}\sigma}\leq\alpha\right)\rightarrow\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\alpha}e^{-\frac{x^2}{2}}dx\quad(n\rightarrow\infty)$$
Therefore: $$ \begin{aligned} S_n&\sim\mathcal{N}\left(n\mu, n\sigma^2\right) & (n\rightarrow\infty)\\ \bar{\mathbf{X}}_n = \left(\mathbf{X}_1+\cdots+\mathbf{X}_n\right)/n&\sim\mathcal{N}\left(\mu,\sigma^2/n\right) & (n\rightarrow\infty) \end{aligned} $$

Proof.¶

We assume that $\bar{\mathbf{X}}_n$ have the "finite" variance $\sigma^2$

Example¶

In [10]:

N = 10000
ns = [10,100,1000,10000]
roll = 4
seed = 0

In [11]:

fig = plt.figure(figsize=(12,6))
ax_all = plt.subplot2grid((2,len(ns)), (0,0), colspan=len(ns))
for i,n in enumerate(ns):
    ax = plt.subplot2grid((2,len(ns)), (1,i))
    dices = np.random.RandomState(seed).randint(low=1, high=6+1, size=(n,N))
    rate_dice_eq_4 = np.count_nonzero(dices==roll, axis=1)/N
    freqs, bins, patches = ax.hist(rate_dice_eq_4, bins=20, density=True)
    cent_bins = [np.mean(bins[i:i+2]) for i in range(len(bins)-1)]
    ax_all.plot(cent_bins, freqs, label=f"n={n}")
    ax.set_title(f"n={n}")
    ax.set_xlabel(f"Probability of {roll} roll.")
    ax.set_ylabel("freq")
ax_all.set_title("Central Limit Theorem")
ax_all.legend()
plt.tight_layout()
plt.show()

Section2.2 ChIP-seq Peak Detection¶

ChIP-sequencing, also known as ChIP-seq, is a method used to analyze protein interactions with DNA. ChIP-seq combines chromatin immunoprecipitation (ChIP) with massively parallel DNA sequencing to identify the binding sites of DNA-associated proteins. It can be used to map global binding sites precisely for any protein of interest. Previously, ChIP-on-chip was the most common technique utilized to study these protein–DNA relations.

Peak calling¶

Problem: How to identify transcription factor binding sites and histone modification enriched regions?

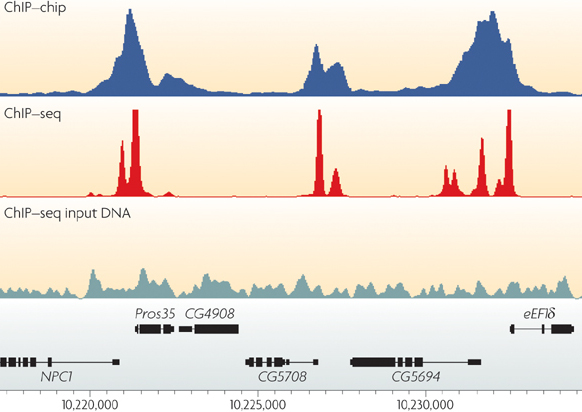
Chip-Seq

Random Read Model¶

Assume that read appears with equal probability in any region.
Calcurate the p-value(the Probability of obtaining more or equally extreme value than observed value under the random model.) → Smaller is more significant.
Setting the threshold (p-value) manually.
We could calcurate the threshold ($n_{obs}$) → If the $n_{obs}$ exceeds this threshold, it is determined as the peak region.

In [12]:

from scipy.special import comb

In [13]:

g = 10000 # total DNA length
n = 1000  # total number of reads
l = 100   # bin size
q = l/g
n_bins = g/l
lambda_ = n*q # mean read count
seed = 0
xmax = 30

In [14]:

fig = plt.figure(figsize=(12,4))

axL = fig.add_subplot(1,2,1)
read_points = np.random.RandomState(seed).randint(0,g, size=n)
axL.scatter(read_points, np.zeros(shape=n), s=3, label="read", color="black")
ledge = 0
read_counts=[]
for edge in range(l,g+1,l):
    middl = (ledge+edge)/2
    count = np.count_nonzero([(ledge<=read_points) & (read_points<edge)])
    read_counts.append(count)
    if edge<=l*10:
        axL.axvline(edge, color="red") 
        axL.text(x=middl,y=1e-3,s=count,horizontalalignment='center')
    ledge = edge
axL.set_xlim(0,l*10)
axL.set_ylim(-1e-3,2e-3)
axL.set_yticks([])
axL.legend()

Poisson = [comb(n,i,exact=True)*(q**i)*((1-q)**(n-i)) for i in range(n)]
axR = fig.add_subplot(1,2,2)
axR.plot(Poisson, color="black", label="Pois($\lambda$)")
axR.plot([read_counts.count(i)/n_bins for i in range(n)], color="red", label="Observed")
axR.set_xlim(0,xmax)
axR.set_xlabel("Read count for each bin")
axR.set_ylabel("Frequency")
axR.legend()

plt.show()

In [15]:

n_obs = 15
p_values = np.cumsum(Poisson[::-1])[::-1] # Calcurate p-value for each n_obs.
thresh_p = 1e-2
bp = np.argmax(p_values<=thresh_p)

In [16]:

fig = plt.figure(figsize=(12,4))

axL = fig.add_subplot(1,2,1)
axL.plot(Poisson, color="black", label="Pois($\lambda$)")
axL.fill_between(np.arange(n_obs, xmax),y1=Poisson[n_obs:xmax],y2=0,facecolor='red')
axL.annotate(
    'p-value \n= $\mathbb{P}(n_{obs}\leq N)$\n$=\sum_{i=n_{obs}}^{\infty}(\lambda^i/i!)\cdot e^{-\lambda}$', 
    xy=(17,1e-2), xytext=(20,4e-2), fontsize=12,
    arrowprops=dict(width=1,headwidth=8,headlength=10, connectionstyle='arc3',facecolor='black')
)
axL.set_xlim(0,30)
axL.set_title("Poisson distribution")
axL.set_xlabel("N")
axL.set_ylabel("Freq")

axR = fig.add_subplot(1,2,2)
axR.plot(p_values, color="black")
axR.scatter(n_obs,p_values[n_obs],color="red",label="pvalue($n_{obs}$="+f"{n_obs})")
axR.scatter(bp,p_values[bp],color="blue",label="Boundary point")
axR.axhline(thresh_p, color="blue", label=f"threshold(p_value={thresh_p})")
axR.axvspan(xmin=bp, xmax=xmax, color="blue", alpha=0.3)
axR.set_xlim(0,xmax)
axR.set_title("The relationship between p-value and $n_{obs}$")
axR.set_xlabel("$n_{obs}$")
axR.set_ylabel("p-value")
axR.legend()

plt.show()

In this case, we could say the threshold($n_{obs}$) = 19(=bp).

※ In ChIP-seq, we have to do "Tag shift" due to the DNA strand asymmetry.（→ more:MACS）

Section2.3 Hypothesis Testing¶

Terminology¶

In [17]:

fig, ax = plt.subplots(figsize=(6,4))
X = np.arange(10,100,1)
Y = 1/X

# Null distribution
ax.plot(X,Y,color="red"), ax.text(x=15, y=8e-2, s="Null distribution\n $f_S(s|H)$", fontsize=15)
# Thereshold: Sα
ax.plot((50,50),(0,7e-2), color="black"), ax.text(x=48,y=7.5e-2,s="$S_{α}$",fontsize=12)
# Reject & Accept
ax.annotate('', xy=(75,5e-2), xytext=(52,5e-2), arrowprops=dict(arrowstyle="->", connectionstyle='arc3')), ax.text(x=55, y=5.5e-2, s="reject",fontsize=12) # Reject
ax.annotate('', xy=(25,5e-2), xytext=(48,5e-2), arrowprops=dict(arrowstyle="->", connectionstyle='arc3')), ax.text(x=35, y=5.5e-2, s="accept",fontsize=12) # Accept
# Observation sample.
ax.plot((70,70),(0,1/70),color="black"), ax.scatter(70,1/70,color="black"), ax.text(x=68,y=2e-2,s="$S_{obs}$",fontsize=12)

ax.set_xticks([]), ax.set_yticks([])
ax.set_xlabel("S"), ax.set_ylabel("freq")
ax.set_xlim(min(X),max(X)), ax.set_ylim(min(Y),max(Y))
plt.show()

Null Hypothesis $H_0$
Alternative Hypothesis $H_1$
Test Static $S$
Null distribution
Significance threshold
Reject/Accept $H_0$

	Null hypothesis is True	Null hypothesis is False
Do not reject Null hypothesis ($H_0$)	Correct	Type2 error (False negative)
Reject Null hypothesis ($H_0$)	Type1 error (False positive)	Correct

P-value distribute uniformly under $H_0$¶

Proof.¶

p-value is the probability of obtaining more or equally extreme value than observed value under the null distribution. $$p = \mathbb{P}\left(S\geq s|H_0\right) = 1-\mathbb{P}\left(S< s|H_0\right)$$
By noting $F_0$ the cumulative distribution function of $S$ under $H_0$, we obtain: $$p = 1-F_0(s)$$
Thanks to the fact that the cdf is monotonic, increasing and (left-)continuous: $$\mathbb{P}\left(S\geq s|H_0\right) = \mathbb{P}\left(F_0\left(S\right)\geq F_0\left(s\right)\right) = 1-\mathbb{P}\left(F_0\left(S\right)< F_0\left(s\right)\right)$$
Therefore, we have: $$\mathbb{P}\left(F_0\left(S\right)< F_0\left(s\right)\right) = F_0\left(s\right)$$

Which means that $F_0\left(S\right)$ is following a uniform distribution. And, as this means also that $1-F_0\left(S\right)$ is following a uniform distributed, then we can conclude that p-value are uniformly distributed under the null hypothesis.

In [18]:

from scipy.stats import norm

In [19]:

N = 10000
loc=0
scale=1
seed = 0

In [20]:

obs = np.random.RandomState(seed).normal(loc=loc, scale=scale, size=N) # observation sample "s".
p_value = 1-norm.cdf(x=obs, loc=loc, scale=scale) # p-value = 1 - F(s)

In [21]:

fig=plt.figure(figsize=(12, 4))

axL = fig.add_subplot(1,2,1)
freqs, bins, patches = axL.hist(obs, bins=50, density=True, color="blue", alpha=0.7)
cent_bins = [np.mean(bins[i:i+2]) for i in range(len(bins)-1)]
axL.plot(cent_bins, freqs, color="blue")
axL.set_title("Histogram of observation sample s\n under the null distribution (This time: Normal distribution)"), axL.set_xlabel("observation s"), axL.set_ylabel("Frequency")

axR = fig.add_subplot(1,2,2)
axR.hist(p_value, bins=20, edgecolor="black")
axR.set_title("Histogram of p-value"), axR.set_xlabel("p-value"), axR.set_ylabel("Frequency")

plt.tight_layout()
plt.show()

※ We could argue about the p-value under the null hypothesis, but we could not confirm whether null hypothesis is true or not.

Section2.4 Hypothesis Test Example¶

$\chi^2$-test¶

Any statistical hypothesis test where the sampling distribution of the test statistic is a chi-squared distribution when the null hypothesis is true.
Used to determine whether there is a significant difference between the expected frequencies and the observed frequencies in one or more categories.

$\chi^2$-distribution¶

$Y_i\sim\mathcal{N}\left(0,1\right), i=1,\ldots,\nu$: i.i.d.
$X=Y_1^2+\cdots+Y_{\nu}$
$\rightarrow X\sim\chi^2(\nu), X\in \mathbb{R}_{\geq0}$ $$ \begin{aligned} f_X(x) &= \frac{1}{2^{\nu/2}\Gamma(\nu/2)}x^{\nu/2-1}e^{-x/2}\\ \Gamma(z) &= \int_{0}^{\infty}t^{z-1}e^{-t}dt(\mathrm{Re}(z)>0)\\ \mathbb{E}(X) &= \nu\\ \mathbb{V}(X) &= 2\nu \end{aligned} $$

In [22]:

from scipy.stats import chi2

In [23]:

K = 5

In [24]:

fig = plt.figure(figsize=(6,4))

X = np.linspace(0, 8, 1000)
for k in range(1,K+1):
    plt.plot(X, chi2.pdf(X, k), label=f"$k={k}$")
    
plt.xlim(0, 8), plt.ylim(0, 1.0)
plt.title("$\chi^2$-distribution"), plt.xlabel("X"), plt.ylabel("P(X)")
plt.legend()
plt.show()

Pearson's chi-square test¶

goodness of fit test¶

#	$C_1$	$C_2$	$\cdots$	$C_k$	total
Observation frequency	$n_1$	$n_2$	$\cdots$	$n_k$	$n$
Theoretical probability (under $H_0$)	$p_1$	$p_2$	$\cdots$	$p_k$	$1$
Theoretical frequency	$m_1=np_1$	$m_2=np_2$	$\cdots$	$m_k=np_k$	$n$

Null Hypothesis($H_0$): $P(C_i) = p_i\quad(i=1,2,\ldots,k)$
If null hypothesis is true, $U$ are distributed as $\chi^2(k-1)$.

$$ U=\sum_{i=1}^k\frac{(n_i-m_i)^2}{m_i}\\ \begin{cases} U&>\chi_{\alpha}^2(k-1) &\Rightarrow \text{Reject }H_0\\ U&\leq\chi_{\alpha}^2(k-1) &\Rightarrow \text{Accept }H_0 \end{cases} $$

test for independence¶

A\B	$B_1$	$B_2$	$\cdots$	$B_b$	total
$A_1$	$n_{11}$	$n_{12}$	$\cdots$	$n_{1b}$	$n_{1\cdot}$
$A_2$	$n_{21}$	$n_{22}$	$\cdots$	$n_{2b}$	$n_{2\cdot}$
$\vdots$	$\vdots$	$\vdots$	$\cdots$	$\ddots$	$\vdots$
$A_a$	$n_{a1}$	$n_{a2}$	$\cdots$	$n_{ab}$	$n_a$
total	$n_{\cdot1}$	$n_{\cdot2}$	$\cdots$	$n_{\cdot b}$	$n_{a\cdot}$

$P(A_i) = p_i,P(B_j)=q_j,\quad (1\leq i\leq a,1\leq j\leq b)$
Null Hypothesis($H_0$): $A$ and $B$ are independence. $$P(A_i\cap B_j) = p_iq_j$$
If null hypothesis is true, we could presume:
- $\bar{p_i}=n_{i\cdot}/n$, $\bar{q_j}=n_{\cdot j}/n$.
- $m_{ij} = n\bar{p_i}\bar{q_j}$ (Theoretical frequency)

$$ U=\sum_{i=1}^a\sum_{j=1}^b\frac{(n_{ij}-m_{ij})^2}{m_{ij}}\\ \begin{cases} U&>\chi_{\alpha}^2\left((a-1)(b-1)\right) &\Rightarrow \text{Reject }H_0\\ U&\leq\chi_{\alpha}^2\left((a-1)(b-1)\right) &\Rightarrow \text{Accept }H_0 \end{cases} $$

t-test¶

One-sample test: Determine whether a sample of observations could have been generated by a process with a specific mean $\mu$.
Two-sample test: Compare the average values of the two data sets and determine if they came from the same population.

t-distribution¶

$$ \begin{aligned} f_{t(\nu)}(x) &= \frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\sqrt{\nu\pi}\Gamma\left(\frac{\nu}{2}\right)}\left(1+\frac{x^2}{\nu}\right)^{-\frac{\nu+1}{2}}\\ \mathbb{E}(X) &= 0(\nu>1)\\ \mathbb{V}(X) &= \begin{cases}\infty&(1<\nu\leq2)\\\frac{\nu}{\nu-2}&(2<\nu)\end{cases} \end{aligned} $$

In [25]:

from scipy.stats import t as tdist

In [26]:

fig = plt.figure(figsize=(6,4))

X = np.linspace(-6, 6, 1000)
nus = [1, 2, 5, 1000]
for nu in nus:
    plt.plot(X, tdist.pdf(X, nu), label=f"$ν={nu}$")
plt.plot(X, norm.pdf(X, 0, 1), linestyle=':', linewidth=5, label="Standard Normal Distribution")

plt.xlim(-6, 6), plt.ylim(0, 0.4)
plt.title("t-distribution"), plt.xlabel("X"), plt.ylabel("P(X)")
plt.legend()
plt.show()

Student's t-test¶

One-sample test: $$ X_1,\ldots,X_n\sim\mathcal{N}(\mu,\sigma)\text{: i.i.d.}\\ \bar{X} = \frac{X_1,\ldots,X_n}{n}, S = \frac{\left(X_1-\bar{X}\right)^2 + \cdots+\left(X_n-\bar{X}\right)^2}{n-1}\\ \rightarrow T=\frac{\left(\bar{X}-\mu\sqrt{n}\right)}{S}\sim t(n-1) $$
Two-sample test (when we know two groups have equal variance): $$ X_{11},\ldots,X_{1m}\sim\mathcal{N}(\mu,\sigma_1)\text{: i.i.d.}, \bar{X}_1 = \frac{X_{11}+\cdots+X_{1m}}{m}\\ X_{21},\ldots,X_{2n}\sim\mathcal{N}(\mu,\sigma_2)\text{: i.i.d.}, \bar{X}_2 = \frac{X_{21}+\cdots+X_{2n}}{n}\\ S=\frac{\sum_{i=1}^m\left(X_{1i}-\bar{X}_1\right)^2 + \sum_{i=1}^n\left(X_{2i}-\bar{X}_2\right)^2}{m+n-2}\\ \rightarrow T=\frac{\left(\bar{X}_1-\bar{X}_2\right)\sqrt{mn}}{S\sqrt{m+n}}\sim t(m+n-2) $$
Two-sample test (when we know two groups have equal variance): $$ X_{11},\ldots,X_{1m}\sim\mathcal{N}(\mu,\sigma_1)\text{: i.i.d.}, \bar{X}_1 = \frac{\sum_{i=1}^mX_{1i}}{m}, S_1 = \frac{\sum_{i=1}^m\left(X_{1i} - \bar{X}_1\right)^2}{m-1}, A=S_1/m\\ X_{21},\ldots,X_{2n}\sim\mathcal{N}(\mu,\sigma_2)\text{: i.i.d.}, \bar{X}_2 = \frac{\sum_{i=1}^mX_{2i}}{n}, S_1 = \frac{\sum_{i=1}^m\left(X_{2i} - \bar{X}_2\right)^2}{n-1}, B=S_2/n\\ \rightarrow T=\frac{\left(\bar{X}_1-\bar{X}_2\right)}{S\sqrt{A+B}}\approx t(\nu), \nu=\frac{(A+B)^2}{A^2/(m-1)+B^2/(n-1)} $$

In [ ]:

生物統計論第2回

Section2.1 Central Limit Theorem¶

Law of Large Numbers¶

Theorem¶

Proof.¶

Chebyshev Inequality¶

Example¶

Exception¶

Cauchy distribution¶

Central Limit Theorem¶

Theorem¶

Proof.¶

Example¶

Section2.2 ChIP-seq Peak Detection¶

Peak calling¶

Random Read Model¶

Section2.3 Hypothesis Testing¶

Terminology¶

P-value distribute uniformly under $H_0$¶

Proof.¶

Section2.4 Hypothesis Test Example¶

$\chi^2$-test¶

$\chi^2$-distribution¶

Pearson's chi-square test¶

goodness of fit test¶

test for independence¶

t-test¶

t-distribution¶

Student's t-test¶

Table of Contents

Published

Last Updated

Category

Tags

Contact

Other contents