import numpy as np
import matplotlib.pyplot as plt
第1問¶
(1)
活動電位は神経細胞膜の膜電位に依存してイオンの透過度が変化することにより生ずる。この際起こるイオン透過性の一連の変化、および、それに応じた膜電位の変化について記述せよ(5~10行程度)。
(1)
活動電位は、膜を挟んだ電荷の劇的な再分配であり、
- 細胞が活動電位を発生している時の脱分極(Depolarization)は、膜を通過する $\mathrm{Na}^{+}$ の流入
- 再分極( Repolarization)は、$\mathrm{K}^+$ の流出
によりそれぞれ生じる。この時の一連の変化を、以下の膜電位の図と対応して記述する。なお、定常状態において、$\mathrm{Na}^{+}$ は細胞外で、$\mathrm{K}^{+}$ は細胞内で濃度が高い。
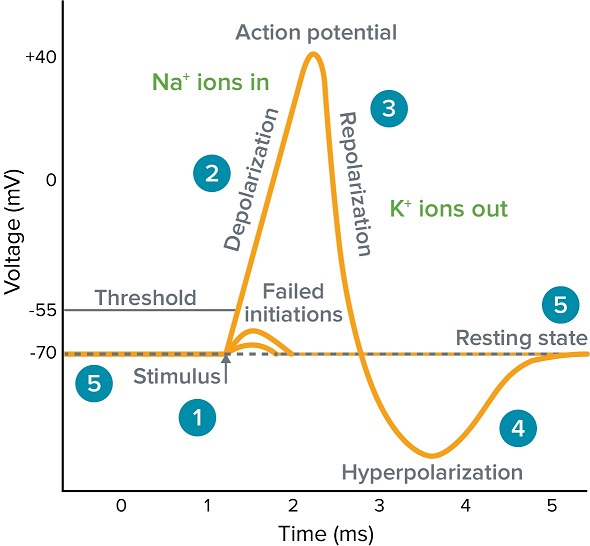 Ref: https://www.moleculardevices.com/applications/patch-clamp-electrophysiology/what-action-potential
Ref: https://www.moleculardevices.com/applications/patch-clamp-electrophysiology/what-action-potential- 外部からの刺激、他のニューロンが放出した神経伝達物質に特異的なチャネルを通過流入するような $\mathrm{Na}^{+}$、などの諸要因によって膜電位が上昇する。この時、膜電位がある閾値を超える脱分極を起こすと、膜にある $\mathrm{Na}$ チャネルが開く。
- $\mathrm{Na}$ チャネルが開くと、細胞内外の濃度勾配によって $\mathrm{Na}^{+}$ がさらに流入し、膜電位が上昇する。
- 正の膜電位になると、$\mathrm{Na}$ チャネルが不活性化し、今度は細胞内外の濃度勾配によって $\mathrm{K}^{+}$ が細胞外へと流出して膜電位が下がる。
- この時、膜電位が静止膜電位よりもさらに負になる過分極( Hyperpolarization)が生じることが知られている。なお、過分極は、ニューロンを不応期にすることで、活動電位が一方向にのみ伝達する仕組みを作っている。
- 静止膜電位に電位が戻る。
この現象を、NESTを用いてシミュレーションする。
import nest
# create Hodgkin-Huxley neuron with delta-shaped synaptic currents.
neuron=nest.Create('hh_psc_alpha')
# create a spike generator
spikegenerator=nest.Create('spike_generator')
# modify spike generation with times 10 and 50 ms
nest.SetStatus(spikegenerator,{'spike_times': [10.,50.]})
# create a voltmeter
voltmeter = nest.Create('voltmeter')
# create add a spikedetector!
spikedetector = nest.Create('spike_detector')
# connect spike generator with a given synaptic specification (weight)
nest.Connect(spikegenerator, neuron, syn_spec={'weight':1e3})
# connect voltmeter to the neuron for measurements
nest.Connect(voltmeter, neuron)
# connect spikedetector to the neuron
nest.Connect(neuron, spikedetector)
### run simulation for 100ms
nest.Simulate(100.)
# read out recording time and voltage from voltmeter (check the parameter list!)
times=nest.GetStatus(voltmeter)[0]['events']['times']
voltage=nest.GetStatus(voltmeter)[0]['events']['V_m']
# plot results
plt.plot(times,voltage)
plt.xlabel('Time (ms)');
plt.ylabel('Membrane potential (mV)')
plt.grid(linestyle='-', linewidth=.25, alpha=.7)
plt.show()
(2)
ホジキンとハクスレーは活動電位の発生機構を研究するため膜電位固定法を用いた。図1は膜電位固定実験下において流れる膜電流のうち、$\mathrm{K}^+$ 成分($I_k$)のみを取り出したものである。膜をさまざまなテスト電位($Vc= 25 \mathrm{mV},\ 60 \mathrm{mV},\ 85\mathrm{mV},\ 100 \mathrm{mV}$)で固定したときの実験データーを示している。
ホジキンとハクスレーはこのような実験データーから活動電位を記述する数理モデルを提出した。講義の内容を踏まえ、以下の問いに答えよ。なお、$\mathrm{K}^+$ コンダクタンスの最大値$\bar{g_k}=83\Omega^{-1}/\mathrm{cm^2}$、$\mathrm{K}^+$ の平衡電位 $\mathrm{E_K}=-80\mathrm{mV}$ とする。
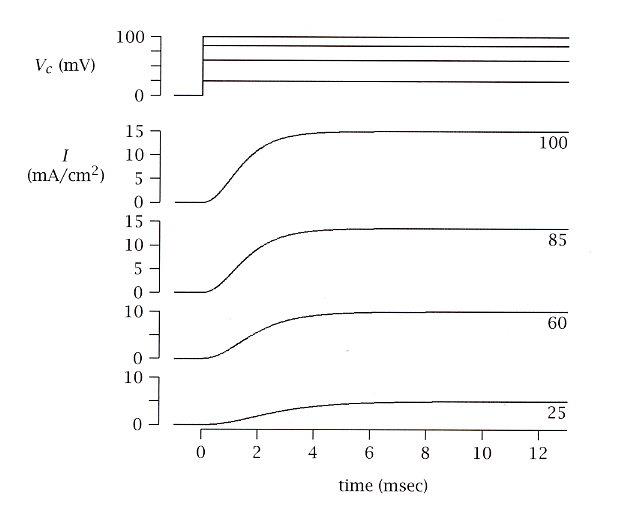
Ek = -80 # mV
gKmax = 83 # Ω^-1/cm^2
Vc = [25, 60, 85, 100] # mV
Ikinf = [25,60,85,100] # mA/cm^2
定常状態($t\rightarrow\infty$)における $\mathrm{K}^+$ コンダクタンス $g_{K_{\infty}}$ を $I_{K_{\infty}},\ Vc, E_K$ で表せ。また $I_{K_{\infty}}$ の実測値より各テスト電位における $g_{K_{\infty}}$ の値を求めよ。
ホジキンとハクスレーの提唱した数理モデルは、$\mathrm{K}^+,\mathrm{Na}^+$ などの各成分を並列等価に繋いだ回路モデルで表され、数式で表現すると
$$ \begin{aligned} g_{Na} &= \frac{I_{Na}\left(V_m,t\right)}{V_m-E_{Na}}\\ g_K &= \frac{I_K\left(V_m,t\right)}{V_m-E_K} \end{aligned} $$となる。したがって、定常状態($t\rightarrow\infty$)における $\mathrm{K}^+$ コンダクタンス $g_{K_{\infty}}$ は、
$$g_{K_{\infty}} = \frac{I_{K_{\infty}}}{V_c-E_K}$$で求められる。また、各テスト電位における $g_{K_{\infty}}$ の値は、
print_func_1a = lambda x,y,z: print(f"|{str(x)}|{str(y)}|{str(z)}|")
print_func(
"$$Vc\ [\mathrm{mV}]$$",
"$$I_{K_{\infty}}[\mathrm{mA/cm^2}]$$",
"$$g_{K_{\infty}}\ [\mathrm{\Omega^{-1}/\mathrm{cm^2}}]$$",
)
print_func(":-:",":-:",":-:")
for i,v in zip(Ikinf, Vc): print_func(v,i,f"{i / (v-Ek):.2f}", )
| $$Vc\ [\mathrm{mV}]$$ | $$I_{K_{\infty}}[\mathrm{mA/cm^2}]$$ | $$g_{K_{\infty}}\ [\mathrm{\Omega^{-1}/\mathrm{cm^2}}]$$ |
|---|---|---|
| 25 | 25 | 0.24 |
| 60 | 60 | 0.43 |
| 85 | 85 | 0.52 |
| 100 | 100 | 0.56 |
ホジキンとハクスレーは $\mathrm{K}^+$ コンダクタンス $g_K$ を $g_K = n^4(t,V)\cdot\bar{g_K}$ と表した(ここで、$n(t,V)$ および以下に出てくる $\tau_n,\alpha_n,\beta_n$ は講義での定義に従う)。定常状態における $n$ の値 $n_{\infty}(V)$ を各テスト電位について求めよ。
題意より、$g_{K_{\infty}} = n_{\infty}^4(t,V)\cdot\bar{g_K}$ と表せるので、
print_func_1b = lambda x,y,z,w: print(f"|{str(x)}|{str(y)}|{str(z)}|{str(w)}|")
print_func_1b(
"$$Vc\ [\mathrm{mV}]$$",
"$$I_{K_{\infty}}[\mathrm{mA/cm^2}]$$",
"$$g_{K_{\infty}}\ [\mathrm{\Omega^{-1}/\mathrm{cm^2}}]$$",
"$$n_{\infty}$$",
)
print_func_1b(":-:",":-:",":-:",":-:")
for i,v in zip(Ikinf, Vc):
gK_inf = i / (v-Ek)
n_inf = pow(gK_inf / gKmax, 1/4)
print_func_1b(v, i, f"{gK_inf:.2f}", f"{n_inf:.2f}")
| $$Vc\ [\mathrm{mV}]$$ | $$I_{K_{\infty}}[\mathrm{mA/cm^2}]$$ | $$g_{K_{\infty}}\ [\mathrm{\Omega^{-1}/\mathrm{cm^2}}]$$ | $$n_{\infty}$$ |
|---|---|---|---|
| 25 | 25 | 0.24 | 0.23 |
| 60 | 60 | 0.43 | 0.27 |
| 85 | 85 | 0.52 | 0.28 |
| 100 | 100 | 0.56 | 0.29 |
となるので、$\tau_n$ は、これからフィッティングすることができる。
パラメータのチューニングをやっていた結果このフィッティングを終えることができませんでした。
以下、速度定数(rate constant) $\alpha_n,\beta_n$ が与えられている場合です。
なお、$n\in[0,1]$ は無次元の係数であり、$\mathrm{K}^+$ コンダクタンスの活性化パラメータ(activation parameter)と呼び、以下の微分方程式で表される。
$$ \begin{aligned} \frac{dn\left(V_m,t\right)}{dt} =&\ \alpha_n\left(V_m\right)\cdot\alpha_n\left(1-n\left(V_m,t\right)\right)\\&- \beta_n\left(V_m\right)\cdot\beta_nn\left(V_m,t\right) \end{aligned}\qquad\cdots(\ast) $$また、$\alpha_n,\beta_n$ は速度定数(rate constant)であり、$\left[t^{-1}\right]$ の次元を持ち、それぞれ以下で表される。
$$ \begin{cases} \begin{aligned} \alpha_n\left(V\right) =&\ \frac{0.01(10-V)}{\exp\left(\frac{10-V}{10}\right)-1}\\ \beta_n\left(V\right) =&\ 0.125\exp\left(-V/80\right) \end{aligned} \end{cases} $$V = np.linspace(-70,50,1000)
alpha = lambda V: 0.01*(10-V)/(np.exp((10-V)/10)-1)
beta = lambda V: 0.125*np.exp(-V/80)
plt.title("The relationship between\n'Membrane potential(V)' and 'alpha','beta' (6.3 degrees Celsius)")
plt.plot(V,alpha(V))
plt.plot(V,beta(V))
plt.xlabel("Membrance potential (mV)"), plt.ylabel("alpha,beta")
plt.grid()
したがって、$n_{\infty}(V)$ は、先の式 $(\ast)$ において $dn/dt=0$ の条件の時に得られるので、
$$n_{\infty}(V) = \frac{\alpha_n\left(V\right)}{\alpha_n\left(V\right)+\beta_n\left(V\right)}$$n_inf = lambda V:alpha(V)/(alpha(V)+beta(V))
第2問¶
(1)
どのようにして記憶は脳内に保持されるのか?その仕組みはまだ完全には分かっていない。しかし、有力な仮説として神経活動の同時性がシナプスの変化として保存されるというものがある(ヘブの原理)。講義の内容を踏まえ、この考え方に沿った記憶の機構について論ぜよ(A4 半分~一枚程度)。
(1)
ヘブ則(Hebbian theory, Hebb's rule)は、
「神経細胞 $A$ の軸索が細胞 $B$ を発火させるのに関与していると考えられるほど近くにあり、繰り返しその発火に関与する時、何かしらの成長過程または代謝変化が一方あるいは両方の細胞に起こり、細胞 $B$ を発火させる細胞の1つとして細胞 $A$ の効率が増加する。」
というものであり、ある神経細胞($A$)の軸索が他の神経細胞($B$)を発火させるパターンが頻繁に生じるのであれば、細胞間の関係(重み)が増し、そのパターンをより伝達しやすくなる、というものである。
なお、ヘブ則はドナルド・ヘブ(Donald Hebb)が1949年に提案したものであり、その後似たような性質として、1997年にスパイクタイミング依存可塑性(spike timing-dependent plasticity, STDP)という仕組みも発見された。これは、
- 神経細胞 $B$ が発火する少し前に神経細胞 $A$ が発火していれば、シナプスが強まる
- 神経細胞 $B$ が発火する少し後に神経細胞 $A$ が発火していれば、シナプスが弱まる
というメカニズムである。
(2)
ヘブの原理を応用した記憶のモデルについて考察しよう。図2のような神経回路を考える。上側から入力する一群の神経($f_1^{\prime}, f_2^{\prime},\ldots,f_j^{\prime},\ldots$:ここでは軸索のみを示している)が、横にならんだ別の群の神経細胞($g_1^{\prime}, g_2^{\prime},\ldots,g_i^{\prime},\ldots$)にシナプスを形成している。
$f^{\prime}$ 神経群の活動をベクトル $\mathbf{f}[f_1,f_2,\ldots,f_j,\ldots]$、$g^{\prime}$ 神経群の活動をベクトル$\mathbf{g}[g_1,g_2,\ldots,g_i,\ldots]$ で表す。また、$f_j^{\prime}$ が $g_i^{\prime}$ 上に作るシナプス(図中の交点)の重みを $a_{ij}$ とし、その総体を行列 $\mathbf{A}[a_{ij}]$ で表す。
ヘブの原理によると、$f_j^{\prime}$ と $g_i^{\prime}$ が同時に活動したときに、その間のシナプス $a_{ij}$ が、$\Delta a_{ij} = k\cdot f_j\cdot g_i$($k$ は定数)で変化する。講義で述べた条件反射に例えると、$f^{\prime}$ が条件刺激、$g^{\prime}$ が無条件刺激に対応した神経群であり、条件刺激と無条件刺激が同時に入力した際、その間のシナプスが強化された結果、学習が成立する。
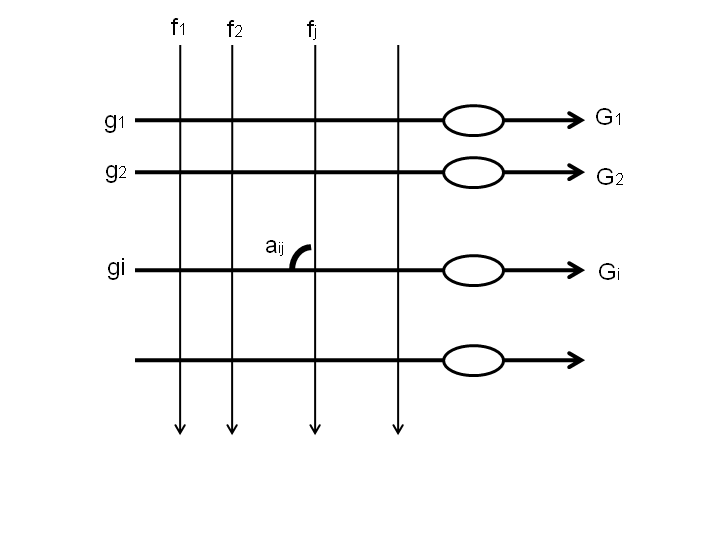
まず具体的な例として、$f^{\prime},g^{\prime}$ それぞれ6 個のニューロンからなる回路において、$\mathbf{A}=\mathbf{0}$ の状態から $\mathbf{f}=[0,0,0, 1, 1, 1], \mathbf{g}=[1,1,0,1,0,0]$ のパターンで同時に活動した時を考える($1$ は神経が活動した状態、$0$ は活動していない状態と考えればよい)。この時ヘブの原理にしたがってシナプスが変化し学習が成立するとした時、学習後の $\mathbf{A}$ を求めよ。ここでは簡単のため $k=1$ とする。
f = np.array([0,0,0,1,1,1])
g = np.array([1,1,0,1,0,0])
A = np.zeros(shape=(g.shape+f.shape))
k = 1
A += k * np.expand_dims(f, axis=0) * np.expand_dims(g, axis=1)
print(A)
上記問aにおいて、学習後に今度は条件刺激にあたる神経群 $f^{\prime}$ の活動のみがあった時を考えよう(記憶成立前に $f^{\prime},g^{\prime}$ 神経群両方が活動した際には、$g^{\prime}$ 神経群は $f^{\prime}$ 神経群からの入力によってではなく他から来る条件刺激により活動したと考える)。
$f^{\prime}$ 神経群からの入力のみがあった場合、神経 $g_i^{\prime}$ の出力 $G_i$ は、
$$G_i = \sum_j a_{ij} \cdot f_j$$となる。記憶成立前と同じパターン $\mathbf{f}=[0,0,0, 1, 1, 1]$ で$f^{\prime}$ 神経群が活動したときの $g^{\prime}$ 神経群の出力 $\mathbf{G}=[G_1,G_2,\ldots,G_i]$ を求め、それが $\mathbf{g}=[1,1,0,1,0,0]$ の整数倍になっている、すなわち記憶のパターンが再現されることを確認せよ。
G = A.dot(f)
print("G:", G.astype(int))
print("g:", g)
記憶のパターンが再現されることが確認できた。
つぎに一般化して考える。上と同様の原理にしたがって、$\mathbf{A}=\mathbf{0}$ の状態から $\mathbf{f}, \mathbf{g}$ のパターンで同時に活動した時、学習成立後の $\mathbf{A}$ は $k\mathbf{g}^T\mathbf{f}$ と表すことができる。このとき、学習後に$f^{\prime}$ 神経群のみが $\mathbf{f}$ のパターンで活動したときの$g^{\prime}$ 神経群の出力 $\mathbf{G}$ を求め、上と同様に記憶が再現されることを示せ。
となり、$\sum_jf_j^2$ は $i$ に依存しないので、$\mathbf{G}$ は $\mathbf{g}$ の $k\sum_jf_j^2$ 倍になることがわかる。
今度は、同じ回路に複数の記憶が同時に蓄えられる場合を考える。すなわち、$\mathbf{f}_i$ と $\mathbf{g}_i$ の同時活動で $A_i= k\mathbf{g}_i^T\mathbf{f}_i$ の記憶が形成され、異なった $\mathbf{f}_i$ と $\mathbf{g}_i$ による記憶が複数起こった総和として、$\mathbf{A} = \sum_iA_i$ となるとする。このとき、複数の記憶が混同せず、再現される(すなわち $\mathbf{G}_i\propto\mathbf{g}_i$)のは、$f^{\prime}$ 神経群の複数の活動 $\mathbf{f}_i$ 間にどのような関係があるときかを考察せよ。
先の式を考えれば、$\mathbf{f}_i$ が直交していれば良いことがわかる。
この回路の性質について自由に考察せよ。
(d)より、全ての記憶を正確に覚えておくには、全ての刺激パターンが直交している必要があった。これを言い換えると、おばあちゃん細胞(grand mother cell)説となる。これは、「ある特定の対象物についての私たちの知覚は、まだ見つかってないどこか究極の知覚領野で少数の特殊化したニューロンが発火するため」と考えるモデルである。
しかし、世の中の記憶すべき対象と神経細胞を一対一に対応させるのは現実的に不可能に思える上、ある神経細胞が死んでしまった時にその対象「だけ」が記憶から抜け落ちてしまう、と考えるのは少し不自然である。その一方で、例えば側頭葉には「ある特定の人物や建物を見た時だけに反応する神経細胞」が見つかっており、この説の真偽は未だ判明していない。
僕は、これに対して、基本的にはヘブ則が成り立っているが、何らかの内部状態が存在し、それによって我々の知覚が多少変化する、というモデルを提唱する。例えば、以下の画像を見る。
この時、何も考えずにこれを見ると「モナリザである」と知覚する。これは、過去の経験からこの絵のようなパターンをモナリザだと記憶しているからである。しかし、この絵を逆さまにすると実はモナリザではないことがわかる。それを確かめた後に再び絵を逆さまにすると、今度は「モナリザではない」と知覚するようになる。
同じ絵を見せられて同じ刺激が入っているはずなのに、別の知覚が生じるが、これもシナプスの重みだとは考えにくい。このように、我々は日々時間 $t$ に依存した状態を持っており、この状態に応じてシナプス間の重みが変化し、知覚も変化する、と考える方が説明能力は高そうである。
Code
import nest
import time
import random
import numpy as np
import matplotlib.pyplot as plt
def plotPatternRaster(spikes, ax=None, cmap="binary_r", **kwargs):
if ax is None: fig,ax=plt.subplots()
H,W = spikes.shape
ax.matshow(spikes, aspect=W/H, cmap=cmap, **kwargs)
ax.set_title("Raster plot of presynaptic neurons"), ax.set_xlabel("time (ms)"), ax.set_ylabel("neuron ID")
return ax
def plotFiringRates(spikes, fig=None):
if fig is None: fig = plt.figure()
num_neurons, _ = spikes.shape
firing_rates = np.mean(spikes, axis=1)*100
neurons_IDs = np.arange(num_neurons)
#=== Plot ===
ax1 = fig.add_subplot(2,1,1)
ax1.barh(neurons_IDs, firing_rates, height=1)
ax1.set_title("Average firing rates of presynaptic neurons"), ax1.set_ylabel("Neuron ID")
ax2 = fig.add_subplot(2,1,2)
ax2.hist(firing_rates)
ax2.set_xlabel("Average firing rate (Hz)"), ax2.set_ylabel("Frequency")
return fig
class PoissonProcessGenerator():
def __init__(self, **params):
if len(params) > 0: self.load_params(**params)
self.repeated=False
self.pattern_repeated_spikes = None
self.simulation_length = None
self.num_presynaptic_neurons = None
def load_params(self, **params):
self.__dict__.update(params)
def generate_spikes(self, simulation_length=1000, num_presynaptic_neurons=2000, seed=None):
"""Poisson Process.
- each presynpatic neuron will emit spikes independently
- generated by a 'Poisson process' which varies randomly in firing rate r in the range of [0,90] Hz
- the rate of change in r is modified by dr where:
- started at 0
- updated randomly from a uniform distribution over [−360,360] Hz/s every millisecond
- clipped to within [−1800,1800] Hz/s
- manually add some additional spikes to guarantee that 'in every 50ms time bin, each neuron spikes at least once.'
~~~~~~~~~
Arguments
@params simulation_length : (int) the length of the simulation processing. (memorize)
@params num_presynaptic_neurons: (int) the number of independent presynaptic neurons. (memorize)
@params seed : (int) If you want to make an experiment replicable.
"""
np.random.seed(seed)
start = time.time()
self.simulation_length = simulation_length
self.num_presynaptic_neurons = num_presynaptic_neurons
spikes = np.zeros(shape=(num_presynaptic_neurons,simulation_length))
spikes[:,0] = np.clip(np.random.poisson(self.starting_Hz/1000), 0, 1)
# ds is randomly picked from a uniform distribution over [−360,+360] Hz/s
ds = np.random.uniform(self.min_ds, self.max_ds, size=(num_presynaptic_neurons, simulation_length))
dr = np.zeros_like(ds)
for t in range(simulation_length-1):
# dr is clipped to within [−1800,1800] (Hz/s)
dr[:,t+1] = np.clip(dr[:,t] + ds[:,t], self.min_dr, self.max_dr)
# r varies beteen [0,90] (Hz)
r = np.insert(dr[:,:-1], 0, self.starting_Hz, axis=1)
for t in range(simulation_length-1):
r[:,t+1] = np.clip(r[:,t] + dr[:,t], self.min_r, self.max_r)
# Manually add some additional spikes to guarantee that
# "in every 50ms time bin, each neuron spikes at least once".
spikes[:,t+1] = np.clip(np.random.poisson(r[:,t+1]/1000), 0, 1)
if t+1>=self.min_span:
mask = np.where(np.sum(spikes[:,t+1-self.min_span:t+1], axis=1)==0)[0]
add_pos = np.random.randint(t+1-self.min_span, t+1, size=len(mask))
for idx,pos in zip(mask,add_pos):
spikes[idx,pos] = 1
self.spikes = spikes
print(f"Processing Time: {time.time()-start:.3f}[s]")
return spikes
def select_segment(self, seed=None):
"""Preprocessing.
1. Divide the presynaptic spiking activity into segments of 50ms (segment_length)
2. select a random 50ms segment (idx=selection) to be considered as the "pattern"
"""
self.num_segments = int(self.simulation_length/self.segment_length)
selection = np.random.RandomState(seed).randint(1, self.num_segments)
pattern_spikes = self.spikes[:,selection*self.segment_length:(selection+1)*self.segment_length]
self.pattern_spikes = pattern_spikes
self.selection = selection
print(f"Spikes divided into {self.num_segments} segments.")
print(f"{selection}-th segment was selected as a Pattern.")
def memorize(self, spikes, repeated=False):
""" If you already have Poisson Process array (`spont_100s_alt.npy`), you have to memorize it. """
print("[Before]")
print(f"simulation length: {self.simulation_length}")
print(f"Number of the presynaptic neurons: {self.num_presynaptic_neurons}")
print("Memorizing...")
self.num_presynaptic_neurons, self.simulation_length = spikes.shape
if repeated:
self.pattern_repeated_spikes = spikes
self.repeated = True
else:
self.spikes = spikes
self.repeated = False
print("[After]")
print(f"simulation length: {self.simulation_length}")
print(f"Number of the presynaptic neurons: {self.num_presynaptic_neurons}")
def repeat_segment(self, proportion_of_neurons=0.5, frequency_of_patterns=0.25):
if self.repeated:
print("Requirement already satisfied.")
return (None,None)
else:
self.pattern_repeated_spikes = np.copy(self.spikes)
self.repeated_position = np.zeros(self.spikes.shape)
num_repeats = round(frequency_of_patterns*self.num_segments)
idx_repeats = random.sample(range(self.num_segments), num_repeats)
for idx in idx_repeats:
self.pattern_repeated_spikes[0:int(self.num_presynaptic_neurons*proportion_of_neurons), idx*self.segment_length:(idx+1)*self.segment_length] = self.pattern_spikes[0:int(self.num_presynaptic_neurons*proportion_of_neurons),:]
self.repeated_position[0:int(self.num_presynaptic_neurons*proportion_of_neurons),idx*self.segment_length:(idx+1)*self.segment_length] = 1
print(f"Number of spikes added: {np.sum(self.repeated_position)}")
print(f"Spikes are saved as `self.pattern_repeated_spikes`.")
self.repeated = True
return self.pattern_repeated_spikes, self.repeated_position
def generatePoissonNoise(self, frequency=10):
noise = np.random.poisson(frequency/1000, size=(self.spikes.shape))
return noise
def addPoisonNoise(self, frequency=10):
spikes = self.pattern_repeated_spikes if self.pattern_repeated_spikes is not None else self.spikes
noise = self.generatePoissonNoise(frequency=frequency)
self.noise_added_spikes = np.clip(spikes + noise, 0, 1)
print(f"Spikes are saved as `self.noise_added_spikes`.")
return self.noise_added_spikes
class NeuronalNetwork():
def __init__(self, **params):
if len(params) > 0: self.load_params(**params)
self.built = False
def load_params(self, **params):
self.__dict__.update(params)
def build(self, spike_indicies, re=False):
"""build the Neuronal Network
@param spike_indicies: n-th presynaptic_neuron's i-th spike occurs at spike_indicies[n][i]
"""
if re: print("Reset Kernel.")
re = "Re" if re else ""
nest.ResetKernel()
self.num_presynaptic_neurons = len(spike_indicies)
self.spike_generator = nest.Create('spike_generator', self.num_presynaptic_neurons, params=[{"spike_times": np.asarray(spike_idx, dtype=float)+1} for spike_idx in spike_indicies])
self.parrot_neuron = nest.Create('parrot_neuron', self.num_presynaptic_neurons)
self.post_neuron = nest.Create('iaf_psc_alpha')
self.spike_detector = nest.Create('spike_detector')
self.voltmeter = nest.Create('voltmeter', params={'interval': 0.1})
self.spike_indicies = spike_indicies
print(f"{re}Created {self.num_presynaptic_neurons} spike generators.")
print(f"{re}Created {self.num_presynaptic_neurons} parrot neurons.")
print(f"{re}Created 1 post_neuron.")
print(f"{re}Created spike detector.")
print(f"{re}Created voltmeter.")
def addGaussianPackets(self, simulation_length_pulses,
proportion_of_neurons_pulsing,
number_of_pulses,
spikes_per_pulse,
std_spikes_per_pulse,
seed=None):
pulse_center_times = np.random.RandomState(seed).randint(10, simulation_length_pulses-10, number_of_pulses).astype(float)
self.gaussian_pulses = nest.Create("pulsepacket_generator", params={
"pulse_times": pulse_center_times,
"activity": spikes_per_pulse,
"sdev": std_spikes_per_pulse
})
conn_dict = {
'rule': 'fixed_total_number',
'N': int(self.num_presynaptic_neurons/proportion_of_neurons_pulsing)
}
nest.Connect(self.gaussian_pulses, self.parrot_neuron, conn_dict)
def compile(self, synapse_model="static", ex=1, **params):
if self.built: self.build(self.spike_indicies, re=True)
if len(params) > 0: self.load_params(**params)
nest.SetStatus(self.post_neuron, [{"tau_minus": self.tau_LTD}])
nest.Connect(self.spike_generator, self.parrot_neuron, "one_to_one")
syn_dict = self.SynapseModelHandler(name=synapse_model, ex=ex)
nest.Connect(self.parrot_neuron, self.post_neuron, "all_to_all", syn_dict)
nest.Connect(self.post_neuron, self.spike_detector)
nest.Connect(self.voltmeter, self.post_neuron)
print(f"Connected {self.num_presynaptic_neurons} spike generators to {self.num_presynaptic_neurons} parrot neurons. (one-to-one)")
print(f"Connected {self.num_presynaptic_neurons} parrot neurons to 1 post neuron. (all-to-all) Method: {syn_dict['model']}")
print("Connected post neuron to spike detector")
print("Connected voltmeter to post neuron")
self.built = True
def simulate(self, T=1000., ax=None, **plotkwargs):
if ax is None: fig, ax = plt.subplots()
nest.Simulate(float(T))
times = nest.GetStatus(self.voltmeter)[0]['events']['times']
voltage = nest.GetStatus(self.voltmeter)[0]['events']['V_m']
spiketimes = nest.GetStatus(self.spike_detector)[0]['events']['times']
# As the simulation span is larger than reaction length,
# we will modify the voltage to Make it understandable.
for spike in spiketimes:
voltage[(np.abs(np.asarray(times) - spike)).argmin()] = 0.
ax.plot(times,voltage, **plotkwargs)
ax.set_xlabel('Time (ms)'), ax.set_ylabel('Membrane potential (mV)'), ax.grid(linestyle='-', linewidth=.25, alpha=.7)
return ax
def mask_pattern(self, ax, is_pattern, simulation_times):
add_minus_1 = np.insert(arr=np.any(is_pattern[:,:simulation_times], axis=0), obj=0, values=False).astype(int)
masks = add_minus_1[1:] - add_minus_1[:-1]
start_points = np.where(masks == 1)[0]
end_points = np.where(masks == -1)[0]
for s,e in zip(start_points, end_points):
ax.axvspan(s, e, color = "coral", alpha=0.7)
return ax
def plotWeights(self, is_pattern_neuron, ax=None):
if ax is None:
fig, ax = plt.subplots()
pre_to_post_conninfo = nest.GetConnections(self.parrot_neuron, self.post_neuron)
pre_to_post_weights = np.asarray(nest.GetStatus(pre_to_post_conninfo, keys='weight'))
idxes = np.arange(len(pre_to_post_weights))
ax.barh(idxes[~is_pattern_neuron], pre_to_post_weights[~is_pattern_neuron], color="blue", label="Random Neuron")
ax.barh(idxes[is_pattern_neuron], pre_to_post_weights[is_pattern_neuron], color="red", label="Pattern Neuron")
ax.set_xlabel("Synaptic weights"), ax.set_ylabel("Neuron ID."), ax.legend()
return ax
def SynapseModelHandler(self,name,ex):
if ex==1:
SynapseModelDict = {
"static" : {
"model": "static_synapse",
"weight": 0.5,
},
"standard": {
"model": "stdp_synapse",
"weight": 1.0,
"tau_plus": self.tau_LTP,
"mu_plus": self.a_LTP,
"mu_minus": self.a_LTD,
},
"triplet" : {
"model": "stdp_triplet_synapse",
"weight": 1.0,
"tau_plus": self.tau_LTP,
"Aminus": self.a_LTD/2,
"Aminus_triplet": self.a_LTD/10,
"Aplus": self.a_LTP,
"Aplus_triplet": self.a_LTP*10,
},
"FACETS": {
"model": "stdp_facetshw_synapse_hom",
"weight": 0.7,
"tau_plus": self.tau_LTP,
"tau_minus_stdp": self.tau_LTD,
}
}
if name not in SynapseModelDict:
raise ValueError(f"Couldn't understand {name}. Please chose from\033[01m\033[36m '{', '.join(SynapseModelDict.keys())}' \033[0m")
return SynapseModelDict[name]
elif ex==2:
SynapseModelDict = {
"static" : {
"model": "static_synapse",
"weight": 1.0,
},
"standard": {
"model": "stdp_synapse",
"weight": 1.0,
"tau_plus": self.tau_LTP,
"mu_plus": self.a_LTP*1000,
"mu_minus": self.a_LTD/1000,
"Wmax": 5.0
},
"triplet" : {
"model": "stdp_triplet_synapse",
"weight": 1.0,
"tau_plus": self.tau_LTP,
"Aminus": self.a_LTD/2,
"Aminus_triplet": self.a_LTD/10,
"Aplus": self.a_LTP,
"Aplus_triplet": self.a_LTP*10,
"Wmax": 5.0
},
"FACETS": {
"model": "stdp_facetshw_synapse_hom",
"weight": 0.75,
"tau_plus": self.tau_LTP,
"tau_minus_stdp": self.tau_LTD,
"Wmax": 5.0
}
}
if name not in SynapseModelDict:
raise ValueError(f"Couldn't understand {name}. Please chose from\033[01m\033[36m '{', '.join(SynapseModelDict.keys())}' \033[0m")
return SynapseModelDict[name]
poisson_params = {
"min_span": 50, # [ms]
"starting_Hz": 54, # [Hz]
"min_r": 0, # [Hz]
"max_r": 90, # [Hz]
"min_ds": -3.6e-1, # [Hz/ms]
"max_ds": 3.6e-1, # [Hz/ms]
"min_dr": -1.8, # [Hz/ms]
"max_dr": 1.8, # [Hz/ms]
"segment_length": 50, # [ms] Length of 1 Presynaptic spiking segment length.
}
seed = 0
num_presynaptic_neurons = 2000 # Number of the presynaptic neurons.
simulation_length = 1000 # [ms]
poisson_generator = PoissonProcessGenerator()
poisson_generator.load_params(**poisson_params)
spikes = poisson_generator.generate_spikes(simulation_length, num_presynaptic_neurons, seed=seed)
領域を分け、パターンを選択する。
poisson_generator.select_segment(seed=seed)
fig,ax = plt.subplots(figsize=(5,5))
ax = plotPatternRaster(spikes, ax=ax)
plt.tight_layout()
plt.show()
パターンをコピーする。
proportion_of_neurons=0.5
frequency_of_patterns=0.25
pre_spikes_wrepeats, output_identities = poisson_generator.repeat_segment(proportion_of_neurons, frequency_of_patterns)
ポアソンノイズを加える。
frequency = 10 # [Hz]
noise_added_spikes = poisson_generator.addPoisonNoise(frequency=frequency)
fig,ax = plt.subplots(figsize=(5,5))
ax = plotPatternRaster(noise_added_spikes, ax=ax)
plt.tight_layout()
plt.show()
生成された繰り返しパターンを確かめる。
fig,ax = plt.subplots(figsize=(5,5))
ax = plotPatternRaster(noise_added_spikes, ax=ax)
ax = plotPatternRaster(output_identities, cmap="RdGy_r", ax=ax, alpha=0.7)
plt.tight_layout()
plt.show()
simulation_length_100s = 100_000
num_presynaptic_neurons = 2_000
poisson_generator = PoissonProcessGenerator()
poisson_generator.load_params(**poisson_params)
pre_spikes_wrepeats_100s = poisson_generator.generate_spikes(simulation_length_100s, num_presynaptic_neurons, seed=seed)
proportion_of_neurons = 0.5
frequency_of_patterns = 0.25
poisson_generator.select_segment(seed=seed)
pre_spikes_wrepeats, output_identities = poisson_generator.repeat_segment(proportion_of_neurons, frequency_of_patterns)
noise_added_spikes = poisson_generator.addPoisonNoise(frequency=frequency)
repeated_idxes = np.any(poisson_generator.repeated_position, axis=1)
print(f"Pattern shape = {poisson_generator.pattern_spikes.shape}")
print(f"Poisson Process shape = {noise_added_spikes.shape}")
simulation_times = 1000
spike_indicies = [np.where(is_spike)[0] for is_spike in noise_added_spikes==1]
STDP_paramaters = {
'a_LTP' : 0.03125,
'a_LTD' : 0.85 * 0.03125,
'tau_LTP' : 16.8,
'tau_LTD' : 33.7,
}
シナプスの関係性に応じていくつか試す。
model = NeuronalNetwork(**STDP_paramaters)
model.build(spike_indicies)
model.compile(synapse_model="static", ex=1)
ax = model.simulate(T=simulation_times, color="black")
ax = model.mask_pattern(ax, output_identities, simulation_times)
plt.show()
ax = model.plotWeights(repeated_idxes)
plt.show()
model.compile(synapse_model="standard", ex=1)
ax = model.simulate(T=simulation_times, color="black")
ax = model.mask_pattern(ax, output_identities, simulation_times)
plt.show()
ax = model.plotWeights(repeated_idxes)
plt.show()
model.compile(synapse_model="triplet", ex=1)
ax = model.simulate(T=simulation_times, color="black")
ax = model.mask_pattern(ax, output_identities, simulation_times)
plt.show()
ax = model.plotWeights(repeated_idxes)
plt.show()
model.compile(synapse_model="FACETS", ex=1)
ax = model.simulate(T=simulation_times, color="black")
ax = model.mask_pattern(ax, output_identities, simulation_times)
plt.show()
ax = model.plotWeights(repeated_idxes)
plt.show()
パラメータのチューニングが終わりませんでした。
 Ref:
Ref: