import numpy as np
import matplotlib.pyplot as plt
seed = 0
- 階層的クラスタリング(Hierarchical Clustering):
- 凝集型(agglomerative):各データのみを含むクラスタを併合してゆくことでデータの階層構造を作成する。
- 最短距離法
- 最長距離砲
- 群平均法
- ウォード法
- 分割型(divisive):データ集合を分割することで階層を生成する。
- 凝集型(agglomerative):各データのみを含むクラスタを併合してゆくことでデータの階層構造を作成する。
- 非階層クラスタリング:分割の良さを評価する関数(同質性(homogeneity)と分離性(separation))を定め、良い分割を探す。最適解はNP困難なので準最適解を探す。
- クラスタの評価基準(Cluster validity Index)
- 教師なし
- クラスタ内誤差平方和(エルボー法で極度にSSEが落ちるクラスタ数が良い。) $$\operatorname{SSE} = \sum_k\sum_{x\in C_k}\|x-m_i\|^2$$
- Calinski-Harabasz index $$\operatorname{VRC} = \frac{\sum_k n_k\|m_k-m_{all}\|^2}{\sum_j\sum_{x\in C_k}\|x-m_k\|^2}\times\frac{N-k}{k-1}$$
- Dunn index $$\operatorname{DI} = \underset{i=1\cdots n_C}{\min}\left\{\underset{j=i+1\cdots n_C}{\min}\left\{\frac{\underset{x\in C_i,y\in C_j}{\min\{d(x,y)\}}}{\underset{k=1\cdots n_C}{\max}\left\{\underset{x,y\in C_k}{\max}\{d(x,y)\}\right\}}\right\}\right\}$$
- Silhouette coefficient
$$\operatorname{Si} = \frac{b_i-a_i}{\max\{a_i,b_i\}}$$
- $a_i$ はデータ $i$ と同一クラスタ内のデータとの距離の平均
- $b_i$ はデータ $i$ が含まれないクラスタのデータとの距離の平均のうち最小値
- 高い値ほど含まれるクラスタに一致し、他のクラスタと離れていると判定。
- シルエット分析:個々のデータのシルエット係数を計算し、各クラスタ別に高い順にプロットされたシルエット図を作成する。
- Shilhouette index:$\operatorname{Sil} = 1/N\sum_i\operatorname{Si}$
- アルゴリズムの例
- $k$-means clustering:
- $k$個のクラスタの重心との距離から各点を分類。
- 更新されたクラスタから再度重心を求める。
- 重心が収束するまで1,2を繰り返す。
- DBSCAN:データを隣接点の数から3種に分類しクラスタリングする。
- Mean-shift:密度分布の極大を探す。一定半径の球の中の平均値へ移動。
- $k$-means clustering:
- 教師あり
- クラスタリング結果を $C = \{C_1,C_2,\cdots,C_k\}$
- 正解のクラスタを $A=\{A_1,A_2,\cdots,A_k\}$
- $C_i$ に含まれる $A_j$ の要素の個数を $X_ij=|C_i\cap A_j|$ とする。
- エントロピー:
- $C_i$ のエントロピー $E_i$ は $$E_i = -\sum_{k}\operatorname{Prob}(A_k|C_i)\log \operatorname{Prob}(A_k|C_i)$$
- 全体のエントロピーは以下で表される。低いほど良いと判定。 $$\sum_k\frac{|C_k|}{N}E_k$$
- 純度:ある正解のクラスタをどの程度含むか?
- $C_i$ の純度 $P_i$ は $$P_i = \frac{1}{|C_i|}\max_k|X_{ik}|$$
- 全てのデータの純度は以下で表される。高いほど良いと判定。 $$\sum_k\frac{|C_k|}{N}P_k$$
- F値:
- 再現度 $R_{hk}$ と精度 $P_{hk}$ を以下のように定義 $$R_{hk} = \frac{\left|A_h\cap C_k\right|}{|A_h|}\quad P_{hk} = \frac{\left|A_h\cap C_k\right|}{|C_k|}$$
- $A_h$ と $C_k$ のF値 $F_{hk}$ は $R_{hk}$ と $P_{hk}$ の調和平均 $$F_{hk} = \frac{2R_{hk}P_{hk}}{R_{hk} + P_{hk}}$$
- 全体のF値は $A_h$ に対して最大になる $k$ を求めて $$F = \sum_{h=1}^K\frac{|A_h|}{N}\max_kF_{hk}$$
- 教師なし
- クラスタの評価基準(Cluster validity Index)
$k$-means法¶
まずは、$k$-means clusteringの実装を行う。
- 長所:
- 原理がわかりやすい。
- 1ステップの計算量が $O(kN)$
- 短所:
- 「次元の呪い」
- 高次元において点が疎になりやすい。
- 次元 $d$ が大きくなるほど、データは中心点から離れ、点の分布は疎になる。
- 半径 $r$ の $d$ 次元ユークリッド球面の体積は $$V_d(r) = \frac{\pi^{d/2}}{\Gamma\left(\frac{d}{2} + 1\right)}r^d$$
- 各辺の長さが $2r$ の超立方体の体積は $$(2r)^d$$
- したがって、超球が超立方体に占める割合は $$V_d(r)/(2r)^d = \frac{\pi^{d/2}}{2^d\Gamma\left(\frac{d}{2} + 1\right)}\underset{d\rightarrow\infty}{\longrightarrow}0$$
- クラスタ数をあらかじめ与える必要がある。
- データが超球状に分布することを仮定している。(ユークリッド二乗距離で測るのならば)
- 初期代表点の選び方に依存する。
- KZZ法(Katsavounidis 1994):最も離れた点を選ぶ。
- K-means++(David Arthur 2007):最近接の中心から遠いほど選ばれやすい。
- ランダムに1点選び、中心とする。
- 各点 $x$ に対し、最近接の中心との距離を $D(x)$ とし点 $x_i$ を確率 $\frac{D(x_i)^2}{\sum_i D(x_i)^2}$ で新たな中心として選ぶ。
- 2を繰り返して $k$ 個の中心を初期値として選ぶ。
- 「次元の呪い」
$k$-means法の亜種¶
- kernel $k$-means:$k$-meansの評価関数をカーネルを使用して行う。非線形関数でデータを高次元に写像してクラスタを作成することが可能。
- spectral clustering:データからグラフを作成し、グラフの行列表現の固有値を解き、固有ベクトルのクラスタリングをすることで分類する手法。(重み付きkernel $k$-meansとnormalized cutのspectral clusteringが等価であることが示されている → Kernel k-means, Spectral Clustering and Normalized Cuts)
Q.1 Lloydのk-means実装
- $K$ 個のクラスタにデータを分類するプログラムの実装
- 入力:$K$ 個のクラスタにデータを分類する実数データ
- 出力:データの各クラスタへの分類結果
- 乱数データを生成し、「データの性質(次元・データ数・クラスタ数)」と「計算時間・誤差二乗平均・ループ回数」の関係性の測定
- 超球内に一様分布したデータをクラスタリングする。
- ランダムに設定した複数の中心の、超球体により構成されたデータで計測
- k-means++の実装
解答
1¶
# データの取得
! wget https://mlab.cb.k.u-tokyo.ac.jp/~ichikawa/cluster/three_clusters.txt
with open("three_clusters.txt", "r") as f:
three_clusters_data = np.asarray([line.strip("\n").split("\t") for line in f.readlines()], dtype=float)
print(f"data.shape={three_clusters_data.shape}")
from kerasy.ML.EM import KMeans
model = KMeans(n_clusters=3, random_state=seed)
model.fit(three_clusters_data)
model.silhouette(three_clusters_data)
2¶
※ 超球体内部に一様分布する乱数は、ギブスサンプリングにより生成する。
なお、これから先の実行時間については、以下のプログラムファイルを用いた。
# file 群を整える。
$ tree kadai07
kadai07/
├── kadai07.py
├── kadai07.sh
├── kerasy (https://github.com/iwasakishuto/Kerasy)
└── output
├── Elkan.txt
├── Hamerly.txt
├── Lloyd_Random.txt
└── Lloyd_k++.txtkadai07.py#coding: utf-8
import subprocess
import argparse
import numpy as np
from kerasy.ML.sampling import GibbsMsphereSampler
from kerasy.utils import measure_complexity
from kerasy.ML.EM import KMeans, HamerlyKMeans, ElkanKMeans
ModelHandler = {
'Lloyd_Random': KMeans,
'Lloyd_k++' : KMeans,
'Hamerly' : HamerlyKMeans,
'Elkan' : ElkanKMeans,
}
dimensions = [2,10,100]
sample_nums = [1000,10000,100000]
cluster_nums = [10,100,1000]
repetitions = 10
if __name__ == "__main__":
parser = argparse.ArgumentParser()
parser.add_argument("-m", "--model", choices=['Lloyd_Random', 'Lloyd_k++', 'Hamerly', 'Elkan'])
parser.add_argument("-s", "--seed", type=int, default=0)
args = parser.parse_args()
init = "random" if 'Lloyd_Random' else 'k++'
Model = ModelHandler[args.model]
seed = args.seed
def func(data, n_clusters, random_state):
model = Model(n_clusters, init=init, random_state=random_state)
model.fit(data, verbose=-1)
inertia = model.inertia_
n_iter = model.iterations_
return (inertia, n_iter)
print(f"#dimensions : {dimensions}")
print(f"#sample_nums : {sample_nums}")
print(f"#cluster_nums: {cluster_nums}")
print(f"#repetitions : {repetitions}")
print(f"#seed : {seed}")
print("num_samples, dimensions, num_clusters, processing_time, num_iterations, MSE")
for d in dimensions:
sampler = GibbsMsphereSampler(d, r=1)
for n in sample_nums:
data = sampler.sample(n, random_state=seed, verbose=-1)
for k in cluster_nums:
p_time, metrics = measure_complexity(func, data=data, n_clusters=k, random_state=seed, repetitions_=10)
inertia, n_iter = np.mean(np.asarray(metrics, dtype=float), axis=0)
print(f"{n}, {d}, {k}, {p_time}, {n_iter}, {inertia/n}")kadai07.sh
# chmod +x kadai07.sh
# sh ./kadai07.sh
LOGDIR="output"
if [ -d $LOGDIR ]; then
echo "Deleted ${LOGDIR}"
rm -r $LOGDIR
fi
echo "Created ${LOGDIR}"
mkdir $LOGDIR
for Model in Lloyd_Random Lloyd_k++ Hamerly Elkan
do
python3 kadai07.py -m $Model -s 0 > output/$Model.txt
donefrom kerasy.ML.sampling import GibbsMsphereSampler
from kerasy.utils import measure_complexity
from kerasy.ML.EM import KMeans
dimensions = [2,10,100]
sample_nums = [1000,10000,100000]
cluster_nums = [10,100,1000]
repetitions = 10
# init="random"
def func_1_2(data, n_clusters, random_state):
model = KMeans(n_clusters, init="random", random_state=random_state)
model.fit(data, verbose=-1)
inertia = model.inertia_
n_iter = model.iterations_
return (inertia, n_iter)
for d in dimensions:
sampler = GibbsMsphereSampler(d, r=1)
for n in sample_nums:
data = sampler.sample(n, random_state=0, verbose=-1)
for k in cluster_nums:
p_time, metrics = measure_complexity(func_1_2, data=data, n_clusters=k, random_state=seed, repetitions_=10)
inertia, n_iter = np.mean(np.asarray(metrics, dtype=float), axis=0)
print(f"n={int(n):<6} d={d:<3} k={k:<4} processing time: {p_time:.3f}[s], n_iter={n_iter:.2f}, mse={inertia/n:.3f}")
※ jupyter notebook上でプログラムを実装すると面倒なので、プログラムの実行結果をDataFrame で表示する。
pd.read_csv("path/to/Desktop/kadai07/output/Lloyd_Random.txt", header=5)
3¶
# init="k++"
def func_1_3(data, n_clusters, random_state):
model = KMeans(n_clusters, init="k++", random_state=random_state)
model.fit(data, verbose=-1)
inertia = model.inertia_
n_iter = model.iterations_
return (inertia, n_iter)
pd.read_csv("path/to/Desktop/kadai07/output/Lloyd_k++.txt", header=5)
$k$-means法の高速化¶
- $k$-means clusteringにおいて、最も計算時間を取るのは各点と代表点との距離計算($O(kN)$)
- 繰り返しステップが進むと代表点の移動距離は減り、各点と最も近い代表点は変化しなくなる。
- この不要な距離計算を行わないことで計算の高速化を行う → 三角不等式(Triangle Inequality)
- 「中心 $c$ の移動距離」 + 「移動前の中心 $c$ との距離」 >= 「移動後の中心 $c^{\prime}$ との距離」より、$\operatorname{dis}\left(\mathbf{c}_p^{\prime},\mathbf{x}\right) < \operatorname{dis}\left(\mathbf{c}_q^{\prime},\mathbf{x}\right)$ の判断が $c^{\prime}$ との距離」**より、$\operatorname{dis}\left(\mathbf{c}_p,\mathbf{x}\right) < \operatorname{dis}\left(\mathbf{c}_q,\mathbf{x}\right)$ を用いることでできる。
- $50$ 次元以上で高速(Elkanの命題):Charles Elkan. Using the triangle inequality to accelerate k-means. ICML, pages 147–153. AAAI Press, 2003.
- $50$ 次元以下で高速(Hamerlyの命題):Hamerly, G. Making k-means even faster. SDM (Symposium on Data Mining) 130-140, 2010.
Hamerlyの命題¶
点 $x_i$ の
- 最近接の重心への距離の上界の一つを $u_i\geq\operatorname{d}\left(x_i, c(\operatorname{cls}(i))\right)$
- 2番目に近い重心への距離の下界の一つを $l_i\leq\min_{j\neq \operatorname{cls}(i)}\operatorname{d}\left(x_i, c(j)\right)$
- 所属するクラスターを $\operatorname{cls}(i)$
- $\operatorname{cls}(i)$ の重心を $c\left(\operatorname{cls}(i)\right)$
- $c\left(\operatorname{cls}(i)\right)$ と最も近い他のクラスタの重心との距離を $s\left(\operatorname{cls}(i)\right) = \min_{j\neq \operatorname{cls}(i)}\left\{\operatorname{d}\left(c\left(\operatorname{cls}(i)\right), c\left(j\right)\right)\right\}$
とする。この時、
- $u_i\leq l_i$
- $u_i\leq s\left(\operatorname{cls}(i)\right)/2$
のどちらかが成立するならば、$x_i$ に最も近いクラスターは重心移動後も $\operatorname{cls}(i)$ のまま。
証明¶
- $u_i\leq l_i$ が成立する時: $$ \begin{aligned} \operatorname{d}\left(x_i, c\left(\operatorname{cls}(i)\right)\right)&\leq u_i &\left(\because \text{ definition.}\right)\\ u_i&\leq l_i & \left(\because \text{ definition.}\right)\\ l_i&\leq\min_{j\neq \operatorname{cls}(i)}\operatorname{d}\left(x_i, c(j)\right) &\left(\because \text{ hypothesis.}\right) \end{aligned} $$
- $u_i\leq s\left(\operatorname{cls}(i)\right)/2$ が成立する時: $$ \begin{aligned} 2u_i&\leq s\left(\operatorname{cls}(i)\right) &\left(\because \text{ hypothesis.}\right)\\ s\left(\operatorname{cls}(i)\right)&\leq\operatorname{d}\left(x_i,c\left(\operatorname{cls}(i)\right)\right) + \min_{j\neq \operatorname{cls}(i)}\operatorname{d}\left(x_i,c(j)\right) & \left(\because \text{ Triangle Inequality.}\right)\\ \operatorname{d}\left(x_i, c\left(\operatorname{cls}(i)\right)\right) &\leq u_i & \left(\because \text{ definition.}\right)\\ \therefore 2u_i&\leq u_i + \min_{j\neq \operatorname{cls}(i)}\operatorname{d}\left(x_i,c(j)\right) \end{aligned} $$
より、どちらの場合でも以下が成立する。
$$\operatorname{d}\left(x_i,c\left(\operatorname{cls}(i)\right)\right)\leq\min_{j\neq \operatorname{cls}(i)}\operatorname{d}\left(x_i, c(j)\right)$$Q.2 高速化手法の実装
- Hamerlyの高速化手法の実装
- 入力:$K$ 個のクラスタにデータを分類する実数データ
- 出力:データの各クラスタへの分類結果
- 初期代表点が同じ場合Lloydのアルゴリズムと等しいクラスタを出力することを確認。
- 乱数データを生成し、「データの性質(次元・データ数・クラスタ数)」と「計算時間・誤差二乗平均・ループ回数」の関係性の測定
- Elkanの高速化手法の実装
解答
1¶
from kerasy.ML.EM import HamerlyKMeans
model = HamerlyKMeans(n_clusters=3, random_state=seed)
model.fit(three_clusters_data)
model.silhouette(three_clusters_data)
2¶
def func_2_2(data, n_clusters, random_state):
model = HamerlyKMeans(n_clusters, init="k++", random_state=random_state)
model.fit(data, verbose=-1)
inertia = model.inertia_
n_iter = model.iterations_
return (inertia, n_iter)
for d in dimensions:
sampler = GibbsMsphereSampler(d, r=1)
for n in sample_nums:
data = sampler.sample(n, random_state=0, verbose=-1)
for k in cluster_nums:
p_time, metrics = measure_complexity(func_2_2, data=data, n_clusters=k, random_state=seed, repetitions_=10)
inertia, n_iter = np.mean(np.asarray(metrics, dtype=float), axis=0)
print(f"n={int(n):<6} d={d:<3} k={k:<4} processing time: {p_time:.3f}[s], n_iter={n_iter:.2f}, mse={inertia/n:.3f}")
pd.read_csv("path/to/Desktop/kadai07/output/Hamerly.txt", header=5)
3¶
Elkanの命題¶
点 $x_i$ の
- 最近接の重心への距離の上界の一つを $u_i\geq\operatorname{d}\left(x_i, c(\operatorname{cls}(i))\right)$
- $j$ 番のクラスタの重心への距離の下界を $l_{ij}\leq\operatorname{d}\left(x_i, c(j)\right)$
- 所属するクラスターを $\operatorname{cls}(i)$
- $\operatorname{cls}(i)$ の重心を $c\left(\operatorname{cls}(i)\right)$
- $A$ の、一つ前のイテレーション時の値を $A^{\prime}$
とする。この時、
- $\frac{1}{2}\operatorname{d}\left(c\left(\operatorname{cls}(i)\right),c(j)\right)\geq u_i$ が成立する時、$\operatorname{d}\left(x_i,c(j)\right)$ を計算する必要がない。
- $l_{ij} = \max\left\{0, l_{ij}^{\prime}-\operatorname{d}\left(c(j), c^{\prime}(j)\right)\right\}$ と下界を計算できる。
※ Hamerlyの手法 では、全てのクラスタ重心への距離の下界の一つ $l_i$ を使用するのに対し、ここではそれぞれのクラスタ重心に対して距離の下界 $l_{ij}$ を保持している
証明¶
- $\frac{1}{2}\operatorname{d}\left(c\left(\operatorname{cls}(i)\right),c(j)\right)\geq u_i$ が成立する時 $\left(j{\neq\operatorname{cls}(i)}\right)$: $$ \begin{aligned} \frac{1}{2}\operatorname{d}\left(c\left(\operatorname{cls}(i)\right),c(j)\right)\geq u_i&\geq\operatorname{d}\left(x_i, c(\operatorname{cls}(i))\right) &\left(\because\text{ definition.}\right)\\ \underset{-\frac{1}{2}\operatorname{d}\left(x_i,c\left(\operatorname{cls}(i)\right)\right)}{\Longleftrightarrow}\frac{1}{2}\operatorname{d}\left(c\left(\operatorname{cls}(i)\right),c(j)\right) - \frac{1}{2}\operatorname{d}\left(x_i,c\left(\operatorname{cls}(i)\right)\right)&\geq\frac{1}{2}\operatorname{d}\left(x_i,c\left(\operatorname{cls}(i)\right)\right)\\ \operatorname{d}\left(x_i,c(j)\right)&\geq\operatorname{d}\left(c\left(\operatorname{cls}(i)\right),c(j)\right) - \operatorname{d}\left(x_i,c\left(\operatorname{cls}(i)\right)\right)&\left(\because\text{ Triangle Inequality.}\right)\\ \therefore\operatorname{d}\left(x_i,c(j)\right) &\geq\operatorname{d}\left(x_i,c\left(\operatorname{cls}(i)\right)\right) \end{aligned} $$
- この下界は、$l_{ij}^{\prime}$ が良い下界で、$j$ 番のクラスタの重心の移動距離が小さいほど良い推定となる。(trivial) $$ \begin{cases} \begin{aligned} \operatorname{d}\left(x_i,c(j)\right) &\geq \operatorname{d}\left(x_i,c^{\prime}(j)\right) -\operatorname{d}\left(c(j), c^{\prime}(j)\right) & \left(\because\text{ Triangle Inequality.}\right)\\ \operatorname{d}\left(x_i,c^{\prime}(j)\right)&\geq l_{ij}^{\prime} & \left(\because\text{ definition.}\right)\\ \end{aligned} \end{cases}\\ \begin{aligned} \operatorname{d}\left(x_i,c(j)\right) &\geq\max\left\{0, \operatorname{d}\left(x_i,c^{\prime}(j)\right) -\operatorname{d}\left(c(j), c^{\prime}(j)\right)\right\}\\ &\geq\max\left\{0,l_{ij}^{\prime} - \operatorname{d}\left(c(j), c^{\prime}(j)\right)\right\} \end{aligned} $$
from kerasy.ML.EM import ElkanKMeans
model = ElkanKMeans(n_clusters=3, random_state=seed)
model.fit(three_clusters_data)
model.silhouette(three_clusters_data)
def func_2_3(data, n_clusters, random_state):
model = ElkanKMeans(n_clusters, init="k++", random_state=random_state)
model.fit(data, verbose=-1)
inertia = model.inertia_
n_iter = model.iterations_
return (inertia, n_iter)
for d in dimensions:
sampler = GibbsMsphereSampler(d, r=1)
for n in sample_nums:
data = sampler.sample(n, random_state=0, verbose=-1)
for k in cluster_nums:
p_time, metrics = measure_complexity(func_2_3, data=data, n_clusters=k, random_state=seed, repetitions_=10)
inertia, n_iter = np.mean(np.asarray(metrics, dtype=float), axis=0)
print(f"n={int(n):<6} d={d:<3} k={k:<4} processing time: {p_time:.3f}[s], n_iter={n_iter:.2f}, mse={inertia/n:.3f}")
pd.read_csv("path/to/Desktop/kadai07/output/Elkan.txt", header=5)
1細胞RNA-seq(scRNA-seq)¶
- 微量なサンプルからcDNAライブラリーを作成する技術の発展により、1細胞単位での遺伝子発現量データを得ることが可能となった。(がん・メタゲノム・細胞系譜・神経生物学など。)
- 各細胞が数千~数万種類の遺伝子発現量のデータを持つscRNA-seq dataを解析するための手法として以下の手法がある。
- 2次元または3次元に次元削減することによる可視化
- 次元削減されたデータをクラスタリングすることによる細胞集団や細胞系譜の同定
- 例として、sc-RNAseqにより線虫(c.elegans)の原腸形成から最終分化細胞に至る発達段階の胚のトランスクリプトームを分析し、「sc-RNAseqの結果から細胞が分化する過程の細胞系譜木の再構成」をおこなったものがある("A lineage-resolved molecular atlas of C.elegans embryogenesis at single-cell resolution")
workflow¶
| Single-cell RNA sequencing workflow | Cell isolation |
|---|---|
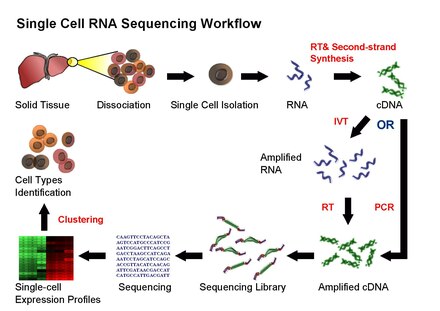 |
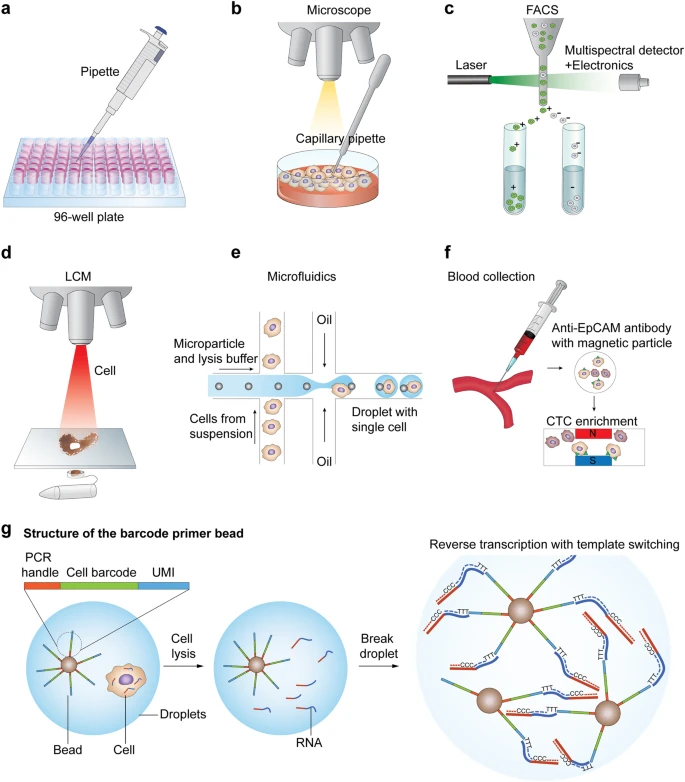 |
Library Preparation¶
| Full-length RNA-seq from single cells using Smart-seq2 | Highly Parallel Genome-wide Expression Profiling of Individual Cells Using Nanoliter Droplets |
|---|---|
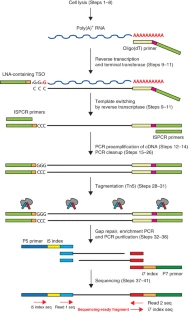 |
 |
次元削減法¶
scRNA-seqの遺伝子発現マトリックスでは各Sampleが高次元の情報を持つためのクラスタリングを行う前に次元削減が必要
- PCA:
- 「データの分散最大化」 or 「次元削減による誤差の最小化」から主成分を求める。
- 線形変換
- t-SNE:
- データ点間の類似度を確率で表し低次元に埋め込む
- 非線形変換
- UMAP:
- 多様体学習を使用した非線型変換
※ scRNA-seqでは、t-SNE, UMAPが可視化のためによく用いられる。
t-SNE¶
- t-distribution: 低次元へ変換したデータ間の類似度を表すために自由度1のt-分布を使用する。
- Stochastic Neighbor Embedding: 高次元空間でのデータ間のユークリッド距離類似度を確率で表現し低次元に変換する。
「データ点間の類似度を表す確率分布」と「低次元に変換した点間の類似度を表す確率分布」を求め、その間のKullback-Leibler divergenceが最小化するように勾配法によって変換後の点の座標を求める手法。
確率分布¶
- 高次元のデータ点 $x_i$ に対するデータ点 $x_j$ の類似度を対象化された結合確率(joint distribution)で表す。 $$p_{ij} = \frac{p_{j|i} + p_{i|j}}{2n}$$
- データ点 $x_j$ は点 $x_i$ を中心とする標準偏差 $\sigma_i$ のガウス分布に比例して選び、条件付確率 $p_{j|i}$ は以下のように求める。 $$p_{j|i} = \frac{\exp\left(-\left\|x_i-x_j\right\|/2\sigma_i^2\right)}{\sum_{k\neq i}\exp\left(-\left\|x_i-x_k\right\|/2\sigma_i^2\right)}$$
- 低次元に変換した点 $y_i$ と点 $y_j$ の類似度を自由度$1$のt分布の同時確率で表す。 $$q_{ij} = \frac{\left(1 + \left\|y_i-y_j\right\|^2\right)^{-1}}{\sum_{k\neq l} \left(1 + \left\|y_k-y_l\right\|^2\right)^{-1}}$$
の$p_{ij}$ と $q_{ij}$ のミスマッチを最小化する。
Perplexity¶
全ての点のガウス分布に対して同じ標準偏差 $\sigma$ を使用するのではなく、「密度の高い領域の点は小さい標準偏差」を「密度の低い領域では大きい標準偏差」を用いる。
ここで、上記の条件を満たすために、データ点 $x_i$ 周辺のデータ密度を表現するPerplexityを以下のように定義する。
$$ \begin{aligned} \text{Perp}\left(P_i\right) &= 2^{H\left(P_i\right)}\\ H\left(P_i\right) &= -\sum_jp_{j|i}\log_2p_{j|i} \end{aligned} $$ここで、
- $\text{Perp}(P_i)$ に対して $H(P_i)$ は単調増加
- $H(P_i)$ に対して標準偏差 $\sigma_i$ は単調増加
より、ガウス分布の標準偏差 $\sigma_i$ が大きいほど、距離が遠い点でも条件付き確率 $p_{j|i}$ が大きな値(negligibleでない)を取ることが多くなる。
Pros and Cons.¶
- 利点:
- Stochastic Neighbor Embeddingからの改善点であり、t-分布の裾が重いため低次元の空間において距離の遠いデータを遠くに配置できる。
- データ間の近さに対称性がある
- 欠点:
- 2,3次元へのマッピング以外では計算コストが高い。
- 局所構造が次元の呪いの影響を受けやすい。
- 最適化アルゴリズムの収束性が保証されていない。
- perplexityの選択により出力に大きな影響がある。
- マッピング後のクラスタ間の距離関係は元の距離を必ずしも反映していない。
DBSCAN¶
- 空間の中で密集している点をクラスタとしてまとめ、疎な領域の点を外れ値とするクラスタリング手法。
- 半径 $\varepsilon$、最小点数 $\text{minPts}$ が与えられた時に、点を $3$ 種類(「コア点」・「到達可能」・「外れ値」)に分類してクラスタリングを行う。
- コア点:点 $P$ を含め半径 $\varepsilon$ 以内に $\text{minPts}$ 個以上の点が存在する点。
- 直接到達可能:コア点 $P$ から $\varepsilon$ 以内にある点 $q$
- 到達可能:コア点 $P_i$ から直接到達可能なコア点 $P_{i+1}$ のパス $P_1P_2\cdots P_nq$ が存在するとき、点 $q$ はコア点 $P_1$ から到達可能。
- 外れ値:どの点からも到達可能でない点
アルゴリズム¶
def DBSCAN(data, epsilon, minPts):
"""
@params data : 点集合
@params epsilon: 半径`epsilon`以内の点を直接到達可能と定義する。
@params minPts : 半径`epsilon`以内に`minPts`個以上の点が存在する場合、コア点とする。
"""
Clusters = []
while(data):
# 未探索の点Pを選ぶ。
p = point_lists.pop()
if p.searched:
continue
# 点pから半径ε以内にある点の個数。
Ps_NeighborPts = p.reacheable(epsilon)
# minPts個以上の点が存在する場合
if minPts <= len(Ps_NeighborPts):
# 点Pを新たなクラスタCに追加する。
cluster = [p]
for q in Ps_NeighborPts:
# 未探索の場合、探索済みにする。
if not q.searched:
q.searched = True
# 点qから半径ε以内にある点の個数。
Qs_NeighborPts = q.reacheable(epsilon)
# minPts個以上の点が存在する場合
if minPts <= len(Qs_NeighborPts):
# 点qから直接到達可能な点の集合を追加する。
Ps_NeighborPts += Qs_NeighborPts
if q not in cluster:
cluster.append(q)
Clusters.append(cluster)
# minPts個未満の点しか存在しない場合
else:
# 探索済みとして終了。
p.searched=True
return Clusters
Pros and Cons.¶
- 利点:
- k-meansと異なり、あらかじめクラスタ数を与える必要がない。
- クラスタが超球状であることを仮定していない。
- 欠点:
- クラスタ間で密度に大きな差がある場合正しくクラスタリングされない。
- パラメータの選択により出力が影響を受ける。
- 高次元では次元の呪いにより半径 $\varepsilon$ の選択が困難。
Q.3 t-SNE+DBSCAN
- 点の集合をDBSCANを用いてクラスタに分類するプログラムの実装
- 入力:データ集合・半径 $\varepsilon$・最小の近接数
minPts - 出力:クラスタへの分類結果
- 入力:データ集合・半径 $\varepsilon$・最小の近接数
- 線虫の細胞系譜の論文 "A lineage-resolved molecular atlas of C. elegans embryogenesis at single-cell resolution" の
gene expression matrix dataのクラスタリング: https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE126954GSE126954_cell_annotation.csvは、各細胞の情報(cell type, embryo time, lineage など。)GSE126954_gene_annotation.csvは、各遺伝子の情報(wormbase での ID と short name.)GSE126954_gene_by_cell_count_matrix.txt.gzは、遺伝子発現マトリックスのデータであり、疎な行列のため、圧縮した書き方をしている。
- その他の細胞種のデータを使用してt-SNEを実行し、DBSCANでクラスタリングを行う。
- GSE126954_gene_by_cell_count_matrix.txtから特定のcell typeのデータを取り出す
- PCAによる次元削減
- t-SNEまたはUMAPによる次元削減
- DBSCANによるクラスタリング
- 各細胞種での遺伝子発現量のヒートマップを作成する
解答
GSE126954_gene_by_cell_count_matrix.txt のデータをクラスタリングする。
- 細胞総数は$89701$個
- 遺伝子総数は$20222$個
celltypeは$37$種類embryo timeのbinは$12$種類
# 全てのデータを取得する場合。
with open('GSE126954_gene_by_cell_count_matrix.txt', mode='r') as f:
header = f.readline() # 1行目は説明
meta_data = f.readline() # 2行目は遺伝子総数・細胞総数・データの行数
lines = [line.strip("\n").split(" ") for line in f] # 3行目以降が (遺伝子番号)(細胞番号)(発現量)の形式のデータ。
gene_data = np.asarray(lines, dtype=np.int)
print(f"data.shape={gene_data.shape}")
特定の細胞種に絞って解析を行う。
import pandas as pd
num_gene = 20222
# 今回注目する細胞種
cell_type = ["Glia", "Intestine", "Seam_cell", "Coelomocyte"]
# アノテーションファイルから、特定の細胞種の細胞idを調べる。
df_cell_anno = pd.read_csv("GSE126954_cell_annotation.csv")
df_cell_used = df_cell_anno[df_cell_anno["cell.type"].isin(cell_type)]
print(f"データ総数: {len(df_cell_anno)}")
print(f"利用するデータ数: {len(df_cell_used)}")
num_cell_type = len(df_cell_used)
# Array の形で保持する。
use_cell_id = np.asarray(df_cell_used.index + 1)
use_cell_type = df_cell_used["cell.type"].to_numpy()
cell_id2idx = dict(zip(use_cell_id, np.arange(num_cell_type)))
# Cell type ごとの細胞数の分布。
df_cell_used.groupby("cell.type").size()
# 取得したidを用いて、抽出。
# (この作業を↑のテキスト読み込み時に行った方が速い)
gene_data_used = gene_data[
np.asarray(list(
map(lambda x: x in use_cell_id, gene_data[:,1])
))
]
# 圧縮されていたので、元の行列の形に直す。
gene_expression_matrix = np.zeros(shape=(num_cell_type, num_gene), dtype=np.int)
for (gene_id, cell_id, val) in gene_data_used:
row = cell_id2idx.get(cell_id)
gene_expression_matrix[row, gene_id-1] = val
# 一度保存(不要)
np.save("GSE126954_gene_by_extracted_cell_count_matrix.npy", gene_expression_matrix)
Decomposition¶
# ロード(不要)
gene_expression_matrix = np.load("GSE126954_gene_by_extracted_cell_count_matrix.npy").astype(float)
num_cell, num_gene = gene_expression_matrix.shape
print(f"データ数: {num_cell}")
print(f"特徴量数: {num_gene}")
from kerasy.utils import CategoricalEncoder
encoder = CategoricalEncoder()
cell_color = encoder.to_categorical(use_cell_type)
def plot_result(X, labels=cell_color, model=None, ax=None, cmap="jet"):
if ax is None:
fig, ax = plt.subplots(figsize=(4,4))
uni_labels = np.unique(labels)
for i,label in enumerate(uni_labels):
ax.scatter(X[labels==label,0], X[labels==label,1], cmap=cmap, label=f"cls{i+1}", s=3, alpha=.7)
ax.legend()
mn = model.__class__.__name__
ax.set_title(f"{mn} result\nnum cluster: {len(uni_labels)}", fontsize=20)
ax.set_xlabel("$x_{" + mn + "1}$", fontsize=16), ax.set_ylabel("$x_{" + mn + "2}$", fontsize=16)
return ax
PCA¶
from kerasy.ML.decomposition import PCA
model_pca = PCA(n_components=2)
model_pca.fit(gene_expression_matrix)
ge_matrix_pca = model_pca.transform(gene_expression_matrix)
plot_result(ge_matrix_pca.real, model=model_pca)
plt.show()
tSNE¶
from kerasy.ML.decomposition import tSNE
model_tsne = tSNE(
initial_momentum=0.5,
final_momoentum=0.8,
eta=500,
random_state=seed
)
ge_matrix_tsne = model_tsne.fit_transform(
gene_expression_matrix,
n_components=2,
initial_dims=50,
perplexity=30.0,
verbose=1,
epochs=500
)
plot_result(ge_matrix_tsne, model=model_tsne)
plt.show()
UMAP¶
from kerasy.ML.decomposition import UMAP
model_umap = UMAP(
min_dist=0.1,
spread=1.0,
sigma_iter=40,
sigma_init=1.0,
sigma_tol=1e-5,
sigma_lower=0,
sigma_upper=np.inf,
)
ge_matrix_umap = model_umap.fit_transform(
gene_expression_matrix,
n_components=2,
n_neighbors=15,
init="random",
epochs=500,
init_lr=1.0,
)
plot_result(ge_matrix_umap, model=model_umap)
plt.show()
Results¶
fig, (ax_pca,ax_tsne,ax_umap) = plt.subplots(1,3,figsize=(18,6))
ax_pca = plot_result(ge_matrix_pca.real, model=model_pca, ax=ax_pca)
ax_tsne = plot_result(ge_matrix_tsne, model=model_tsne, ax=ax_tsne)
ax_umap = plot_result(ge_matrix_umap, model=model_umap, ax=ax_umap)
plt.tight_layout()
plt.show()
Clustering¶
from kerasy.ML.cluster import DBSCAN
tSNE¶
dbscan_tsne = DBSCAN(eps=0.8, min_samples=10)
dbscan_labels_tsne = dbscan_tsne.fit_predict(ge_matrix_tsne)
fig, (ax_tsne, ax_tsne_dbscan) = plt.subplots(1,2,figsize=(12,6))
ax_tsne = plot_result(ge_matrix_tsne, labels=cell_color, model=model_tsne, ax=ax_tsne)
ax_tsne_dbscan = plot_result(ge_matrix_tsne, labels=dbscan_labels_tsne, model=dbscan_tsne, ax=ax_tsne_dbscan)
plt.tight_layout()
plt.show()
UMAP¶
dbscan_umap = DBSCAN(eps=0.5, min_samples=5)
dbscan_labels_umap = dbscan_umap.fit_predict(ge_matrix_umap)
fig, (ax_umap, ax_umap_dbscan) = plt.subplots(1,2,figsize=(12,6))
ax_umap = plot_result(ge_matrix_umap, labels=cell_color, model=model_umap, ax=ax_umap)
ax_tsne_dbscan = plot_result(ge_matrix_umap, labels=dbscan_labels_umap, model=dbscan_umap, ax=ax_umap_dbscan)
plt.tight_layout()
plt.show()
Results¶
fig, ((ax_tsne, ax_tsne_dbscan),(ax_umap, ax_umap_dbscan)) = plt.subplots(2,2,figsize=(12,12))
ax_tsne = plot_result(ge_matrix_tsne, labels=cell_color, model=model_tsne, ax=ax_tsne)
ax_tsne_dbscan = plot_result(ge_matrix_tsne, labels=dbscan_labels_tsne, model=dbscan_tsne, ax=ax_tsne_dbscan)
ax_umap = plot_result(ge_matrix_umap, labels=cell_color, model=model_umap, ax=ax_umap)
ax_tsne_dbscan = plot_result(ge_matrix_umap, labels=dbscan_labels_umap, model=dbscan_umap, ax=ax_umap_dbscan)
plt.tight_layout()
plt.show()