統計的学習理論: PAC learning¶
ここでは二値分類(binary classification)の問題を考える。この問題の目標は、「与えられた訓練データ $(\mathbf{x}_i,y_i): \mathbf{x}_i\in\mathcal{X},y_i\in\{+1,-1\},1\leq i\leq N$ をもとに、良い分類器 $H:\mathcal{X}\rightarrow\{+1,-1\}$ を見つけること」である。
理想的な状況として、「$\mathbf{x}_i$ が $y_i$ を完全に決定している」すなわち「$y_i = c(\mathbf{x}_i)$ となる対応 $c$ が存在する」ような設定を考える。ここで $c$ が任意の関数から選ばれる場合、有限個の学習データから $c$ の値を学習することは不可能となってしまう。つまり、学習が可能であるためには、「$c$ が関数のより小さなクラス $\mathcal{C}$(例えば、「滑らかな」関数)から選ばれている $(c\in\mathcal{C})$」という設定が必要である。このように、問題の学習可能性は、$\mathcal{C}$ の性質として捉えることができる。特に大事なのが、Probably Approximately Correct (PCA) learnableの概念である。
- strong learnability: 任意の $P$、正数 $\epsilon,\delta>0$ に対し、十分な訓練データが利用できれば、汎化誤差 $\epsilon$ 未満となるような分類器を、$1-\delta$ 以上の確率で返せる時、$\mathcal{C}$ はstrong PAC learnableであるという。
- weak learnability: 任意の $P$、正数 $\delta>0$ に対し、十分な訓練データが利用できれば、汎化誤差 $0.5$ 未満となるような分類器を、$1-\delta$ 以上の確率で返せる時、$\mathcal{C}$ はweakly PAC learnableであるという。
なお、AdaBoostは、ブースティング(weakly PAC learnable → strongly PAC learnable)を達成できるアルゴリズムである。
※ 学習データにノイズがある場合、「$\mathbf{x}_i$ が $y_i$ を完全に決定している」という理想的な状況から外れてしまうが、この場合に関しても拡張して論じられている。一方で、この状況において学習で推定するべき $c$ に相当するのは条件付き確率 $P\left(y|\mathbf{x}\right)$ であるとも考えられる。
AdaBoost¶
weak learnability と類似の概念である empirical weak learnability のみ仮定し、AdaBoostが与えられた訓練データに対する訓練誤差をいくらでも小さくできる。
- empirical weak learnability: 任意の訓練データと、任意の重み $w_i(0\leq w_i\leq1)$ に対して、重み付き訓練誤差 $\sum_{i=1}^Nw_i\mathbb{1}\{H(\mathbf{x}_i)\neq y_i\}$ が $0.5$ 未満となる $H$ を選べる。
アルゴリズム¶
- 分類器 $h_t$ を、重み付き訓練誤差 $\sum_{i=1}^Nw_{i,t}\mathbf{1}\{h_t(\mathbf{x}_i)\neq y_i\}$ が $0.5$ 未満となるように選ぶ。
- 重みを更新する:$w_{t+1,i} = w_{t,i}\times\exp\{-\alpha_ty_ih_t(\mathbf{x}_i)\}/Zt$
- ただし、ここで $\alpha_t = (1/2)\times\ln\left((1-e_t)/e_t\right)$
- $Z_t$ は規格化定数で $\sum_i^Nw_{t+1,i} = 1$ が成り立つように決める。
- $T$ 回の繰り返しが終了したら、最後に $H(\mathbf{x}) = \text{sign}\left(\sum_t^T\alpha_th_t(\mathbf{x})\right)$ を返して終了。
def AdaBoost(N, data, T):
""" AdaBoost Algorithm.
@params N : Total data num.
@params data: Training data.| x in X, y in [+1,-1]
@params T : Iteration count.
"""
# Initialization.
W = [1/N for _ in range(N)]
ALPHA = [0 for _ in range(T)]
H = []
# Iteration.
for t in range(T):
# select a classifier "h" whose Weighted training error "e" is smaller than 0.5
h,e = randomSelectClassifier(W)
ALPHA[t] = (1/2) * log((1-e)/e)
W = W * [exp(-alpha[t]*y*h(x)) for (x,y) in data]
Z = sum(W) # Normalized constant.
W = [w/Z for w in W]
H.append(h)
def model(x):
return 1 if sum([alpha*h(x) for (alpha,h) in zip(ALPHA,H)])>=0 else -1
return model
※ randomSelectClassifier がweak learner の仕事である。理論解析が成り立つためにこの関数が必ず成功して分類器を選ぶことが要求されるが、あくまで理論的保証を得るための要求であり、実際には厳密にこれを満たす weak learner が作れないこともある。その場合は、その時点で繰り返しから抜けて最後のモデルを返すのが一般的である。
問1
$Z_t$ を $e_t$ で表す式を導いて、$e_t<1/2$ の時、$Z_t<1$ であることを確かめよ。
解答
$$ \begin{aligned} Z_t &= \sum_i^Nw_{t,i}\times\exp\left(-\alpha_ty_ih_t\left(\mathbf{x}_i\right)\right)\\ &= \sum_i^Nw_{t,i}\times\exp\left(-\alpha_ty_ih_t\left(\mathbf{x}_i\right)\right)\left(\mathbf{1}\left\{h_t(\mathbf{x}_i)\neq y_i\right\} + \mathbf{1}\left\{h_t(\mathbf{x}_i)= y_i\right\}\right)\\ &= e_t\times\exp(\alpha_t) + (1-e_t)\times\exp(-\alpha_t)\\ &= e_t\times\left(\frac{1-e_t}{e_t}\right)^{1/2} + \left(1-e_t\right)\left(\frac{1-e_t}{e_t}\right)^{-1/2}\\ &= 2\sqrt{e_t\left(1-e_t\right)}\\ & < 2\times\sqrt{1/4} = 1\qquad\left(\because0 < e_t < 1/2\right) \end{aligned}\\ $$訓練誤差の評価式¶
ここで、最終分類器 $H$ による訓練誤差は、
$$ \begin{aligned} & \sum_{i}^{N}(1 / N) \mathbf{1}\left\{H\left(\mathbf{x}_{i}\right) \neq y_{i}\right\} \\ =& \sum_{i}^{N} w_{1, i} \mathbf{1}\left\{\operatorname{sign}\left(\sum_{t=1}^T\alpha_th_t\left(\mathbf{x}_{i}\right)\right) \neq y_{i}\right\} \qquad\left(\because w_{1,i}=1/N\right)\\ \leq & \sum_{i}^{N} w_{1, i} \underbrace{\exp \left(-y_{i} \sum_{t=1}^T\alpha_th_t\left(\mathbf{x}_{i}\right)\right)}_{\begin{cases}\geq1 &\text{ if $\operatorname{sign}()\neq y_i$ }\\ > 0 &\text{otherwise.}\end{cases}}\\ = & \sum_i^Nw_{1,i}\prod_{t=1}^T\exp\left(-\alpha_ty_ih_t\left(\mathbf{x}_i\right)\right)\\ = & \sum_i^Nw_{T+1,i}\prod_{t=1}^TZ_t \qquad\left(\because w_{t+1,i}Z_t = w_{t,i}\times\exp\left(-y_i\alpha_th_t\left(\mathbf{x}_i\right)\right)\right)\\ = & \prod_{t=1}^TZ_t\underset{T\rightarrow\infty}{\longrightarrow}0\qquad\left(\because Z_t < 1\right) \end{aligned} $$となるので、最終分類器が、($T$ を十分大きくとれば)任意の精度を実現できる(strong learnability)ことを確認できた。
期待損失最小化とAdaBoost¶
ここで、一見唐突に出現したように見える
$$\alpha_t = (1/2)\times\ln\left((1-e_t)/e_t\right)$$が、以下で定義する指数損失を最小化するという条件を考えると、自然に導かれることを示す。
$t$ ラウンドまで足し合わせた分類器 $H_t(\mathbf{x}) = \sum_{\tau=1}^t\alpha_{\tau}h_{\tau}(\mathbf{x})$ を考えて、$H_t$ の指数損失を
$$l_t:=\sum_i^Nw_{1,i}\exp\left(-y_iH_t(\mathbf{x}_i)\right)$$と定義する。
- 新しく選ばれる分類器 $h_t$ ではなく、計算途中の分類器 $H_t$ に対して考えられている。
- 訓練データごとの重み $w_{t,i}$ は、初期値のままである。
ことに注意する。
$$ \begin{aligned} l_t &= \sum_i^Nw_{1,i}\exp\left(-y_iH_t(\mathbf{x}_i)\right)\\ &= \sum_i^Nw_{1,i}\exp\left(-y_i\sum_{\tau=1}^t\alpha_{\tau}h_{\tau}(\mathbf{x}_i)\right)\\ &= \sum_i^Nw_{1,i}\prod_{\tau=1}^t\exp\left(-y_i\alpha_{\tau}h_{\tau}(\mathbf{x}_i)\right)\\ &= \sum_i^Nw_{1,i}\left(\prod_{\tau=1}^{t-1}\exp\left(-y_i\alpha_{\tau}h_{\tau}(\mathbf{x}_i)\right)\right)\exp\left(-\alpha_ty_ih_t(\mathbf{x}_i)\right)\\ &= \left(\prod_{\tau}^{t-1}Z_{\tau}\right)\sum_i^Nw_{t,i}\exp\left(-\alpha_ty_ih_t(\mathbf{x}_i)\right)\quad \left(\because w_{t,i} = \frac{w_{t-1,i}\exp(-\alpha_{t-1}y_ih_{t-1}(\mathbf{x}_i))}{Z_{t-1}}\right) \end{aligned} $$ここで、この式の $\alpha_t$ に対する依存性を考えると、
$$ \begin{aligned} l_t&\propto\sum_i^Nw_{t,i}\exp\left(-\alpha_ty_ih_t(\mathbf{x}_i)\right)\\ &= \sum_i^Nw_{t,i}\times\exp\left(-\alpha_ty_ih_t\left(\mathbf{x}_i\right)\right)\left(\mathbf{1}\left\{h_t(\mathbf{x}_i)\neq y_i\right\} + \mathbf{1}\left\{h_t(\mathbf{x}_i)= y_i\right\}\right)\\ &= e_t\exp(\alpha_t) + (1-e_t)\exp(-\alpha_t)\\ \end{aligned} $$となるので、
$$Z(\alpha_t) = e_t\exp(\alpha_t) + (1-e_t)\exp(-\alpha_t)$$と定義する。
問2
$Z_t(\alpha_t)$ を $\alpha_t$ について微分して、$Z_t$ を最小にする $\alpha_t$ とそのときの $Z_t$ の値を求めよ。ただし、$e_t$ は $\alpha_t$ からみて定数として考える。
解答
$$ \begin{aligned} \frac{\partial Z_t(\alpha_t)}{\partial\alpha_t} = e_t\exp(\alpha_t) - (1-e_t)\exp(-\alpha_t) &= 0\\ \therefore\exp(-\alpha_t)\left(e_t\exp(2\alpha_t) - (1-e_t)\right) &= 0\\ \exp\left(2\alpha_t\right) &= \frac{1-e_t}{e_t}\\ \therefore\alpha_t &= \frac{1}{2}\ln\left(\frac{1-e_t}{e_t}\right) \end{aligned}\\ $$また、このとき
$$ \begin{aligned} Z(\alpha_t) &= Z\left( \frac{1}{2}\ln\left(\frac{1-e_t}{e_t}\right)\right)\\ &= e_t \sqrt{\frac{1-e_t}{e_t}} + (1-e_t)\sqrt{\frac{e_t}{1-e_t}}\\ &= 2\sqrt{e_t(1-e_t)} \end{aligned}\\ $$したがって、$Z_t$ を最小化するように $\alpha_t$ を選ぶと、$Z_t$ が問1で求めた規格化定数になっていることがわかる。また、$Z_t$ は $l_t$ に比例しているので、AdaBoostが指数損失 $l_t$ を最小化するように $\alpha_t$ を選んでいることがわかる。
$L^2$-Boosting: 回帰問題のためのBoosting¶
AdaBoostの定式化を(ほぼ)同値に言い換えていくことで、回帰のためのBoostingアルゴリズム$L^2$-Boostingが自然に得られることを見ていく。なお、最終的には $y_i\in\mathbb{R}$ として回帰問題を扱いたいが、分類問題の枠組みを維持して $y_i\in\{+1,-1\}$ としておく。
Summary¶
| 手法 | 損失関数 | 補足 |
|---|---|---|
| Coordinate Descent | $$l = \sum_i^n\exp\left(-y_iH(\mathbf{x}_i)\right) = \sum_i^n\exp\left(-y_i\sum_{\lambda}\beta_{\lambda}h_{\lambda}(\mathbf{x}_i)\right)$$ | 各ラウンドで選ぶ $h_t$ が大きさ $L$ の有限集合 $\{h_{\lambda}\}(1\leq\lambda\leq L)$ から選ばれるとする。 |
| Gradient descent algorithm | $$l_t = \sum_i^N\exp\left(-y_i\left(H_{t-1}(\mathbf{x}_i) - \alpha_t\frac{\partial l}{\partial\beta}(\mathbf{x}_i)\right)\right)$$ | 詳しくはhttps://mitpress.mit.edu/books/boosting |
| Functional Gradient Descent | $$\mathcal{L}(H)$$ | $\mathcal{L}(H)$ を選択して、AnyBoostアルゴリズムの形に落とし込む。 |
| AdaBoost | $$\mathcal{L}(H) = \sum_i^N\exp\left(-y_iH(\mathbf{x}_i)\right)$$ | 分類問題の枠組み($\mathcal{Y} = \{+1,-1\}$) |
| LogitBoost | $$\mathcal{L}(H) = \sum_i^N\ln\left(1 + \exp\left(-y_iH(\mathbf{x}_i)\right)\right)$$ | 分類問題の枠組み |
| $L^2$-Boosting | $$\mathcal{L}(H) = \sum_i^N\left(y_i-H(\mathbf{x}_i)\right)^2$$ | 回帰問題の枠組み($\mathcal{Y} = \mathbb{R}$) |
Coordinate Descent法としてのAdaBoost¶
まずは、AdaBoostをCoordinate Descent(座標降下)法という観点から見てみる。
- 簡単のため、各ラウンドで選ぶ $h_t$ が大きさ $L$ の有限集合 $\{h_{\lambda}\}(1\leq\lambda\leq L)$ から選ばれるとする。
- 途中までの分類器 $H_t$ や最終分類器 $H_T$ は $h_{\lambda}$ の線形結合 $\beta_{\lambda}h_{\lambda}$ として表されるので、$\beta_{\lambda}$ を指定すれば完全に定まることになる。
- 最小化すべき指数損失は、次のように表される。 $$l = \sum_i^n\exp\left(-y_iH(\mathbf{x}_i)\right) = \sum_i^n\exp\left(-y_i\sum_{\lambda}\beta_{\lambda}h_{\lambda}(\mathbf{x}_i)\right)$$
- この最小化は、結局 $L$ 個(有限個)のパラメタ $\beta_{\lambda}$ の最適化に帰着する。つまり、各ラウンド $t$ で損失関数が最も減少するように1つのパラメタを選ぶことになる。
- アルゴリズムは、以下のように書ける。なお、このアルゴリズムは、$h_t$ の候補が有限に絞られているという条件を別とすれば、AdaBoostと等価となる。($h_t$ や $\alpha_t$ として同じものが選ばれてくる。)
- 初期化:$H_0=0$ つまり、$\forall\lambda(\beta_{\lambda}=0)$
- $t=1,\ldots,T$ に関して、以下の処理を繰り返す。
- exponential loss $$l_t = \sum_i^N\exp\left(-y_iH_t(\mathbf{x}_i)\right)$$ が最小になるように $\lambda$ と $\alpha_t$ を選ぶ。つまり、更新すべき分類器 $h_{\lambda}$ と、その係数 $\beta_{\lambda}$ の更新幅を決めるということであり、数学的に表すと $$H_t(\mathbf{x}):=H_{t-1}(\mathbf{x}) + \alpha_th_{\lambda}(\mathbf{x})$$ である。$\beta_{\lambda}\leftarrow\beta_{\lambda} + \alpha_t$ と更新したものが $H_t(\mathbf{x})$ とも言える。
- 最後に、以下を返す。 $$H(\mathbf{x}) = \text{sign}\left(H_T(\mathbf{x})\right) = \text{sign}\left(\sum_{\lambda}\beta_{\lambda}h_{\lambda}(\mathbf{x})\right)$$
※ ここまでの議論をまとめると、
$h_t$ が有限の候補から選ばれてくると仮定することで、合成された分類器 $H$ が $h_t$ の線形結合となった
→「$H$ を決めること」が「 $L$ 個の実数値($\beta_{\lambda}$)を指定すること」と等価であった。
→ $H$ 自体を $L$ 次元の実ベクトル $H\in\mathbb{R}^L$ と見なせた。
Functinal Gradient Descent法としてのAdaBoost¶
ここでは、AdaBoostをFunctinal Gradient Descent(汎関数勾配降下)法という観点から定式化してみる。
$h_t$ の候補が有限という仮定を捨てて、$h_t:\mathcal{X}\rightarrow\mathcal{Y}$ という「関数」を決めるのだという態度を明確にする。(関数空間の中で、損失汎関数を最小化する要素を選ぶ。)
- $\mathcal{Y}$ として $\{+1,-1\}$ を取れば分類問題になる。
- $\mathcal{Y}$ として $\mathbb{R}$ を取れば回帰問題になる。
選ばれた関数 $H$ の良し悪しは、損失汎関数 $\mathcal{L}(H)$ によって測る。この値は以下の形をとる。
$$\mathcal{L}(H) = \sum_i^N\text{loss}(\mathbf{x}_i,y_i)$$つまり、$H$ は $\mathbf{x}_i$ で評価した $N$ 個の値 $\left\{H(\mathbf{x}_i)\right\}_{1\leq i\leq N}$ にのみ依存していると考えることができる。そこで、$\mathcal{L}(H)$ を $\mathbb{R}^N$ 上で定義された関数とみなして勾配降下法の発想が適用する。($H(\mathbf{x}_i) =: f_i$ とおいて、$\mathcal{L}\left(f_1,f_2,\ldots,f_N\right)$ の勾配ベクトルを計算できる。)
ここで、一般の勾配法では $-\nabla\mathcal{L}$ の方向に $f_i$ を更新すれば良いので、
$$f_i\leftarrow f_i - \alpha\nabla\mathcal{L}_i$$と更新する。よって、Boostingの場合では
$$H_t(\mathbf{x}_i)\leftarrow H_{t-1}(\mathbf{x}_i) + \alpha_th_t(\mathbf{x}_i)$$と表せる。なお、ここでは $h_t$ を第 $i$ 成分が $h_t(\mathbf{x}_i)$ の $N$ 次元ベクトルと考えて、$H_{t-1}$ で評価した $\nabla\mathcal{L}$ と $h_t$ が平行となるように $h_t$ を選んでいる。
しかし、$h_t$ としてそのようなものが存在するとは限らない。そこで、次善の策として、「$h_t$ の向きが $\nabla\mathcal{L}$ に最も近いもの」を探す。ベクトルの向きの近さは内積を利用することで、
$$ (-\nabla \mathcal{L}) \cdot \frac{h_{t}}{\left\|h_{t}\right\|}=\left.\frac{-1}{\left\|h_{t}\right\|} \sum_{i}^{N} \frac{\partial \mathcal{L}}{\partial f_{i}}\right|_{f_{i}=H_{t-1}(\mathbf{x}_i)} h_{t}\left(\mathbf{x}_{i}\right) $$で測れるので、これの絶対値が最大となる $h_t$ を選び、実係数 $\alpha_t$ を掛けて $H_{t-1}$ に足せば良い。このようにして更新に用いる $h_t$ を選んで得られるのが、Functional Gradient DescentによるAnyBoostアルゴリズムである。
- $(-\nabla \mathcal{L}) \cdot \frac{h_{t}}{\left\|h_{t}\right\|}$ の絶対値が最大となる $h_t$ を選ぶ。
- $\mathcal{L}\left(H_{t-1} + \alpha_th_t\right)$ が最小となる $\alpha_t$ を選ぶ。
- $H_t = H_{t-1} + \alpha_th_t$ と更新する。
- 最後に $H=H_T$ を返す。
$L^2$-Boostingの導出¶
$L^2$-Boostingとは、AnyBoostにおいて損失関数を $L^2$ 損失(自乗誤差)としたものに他ならない。
$$ \begin{cases} \begin{aligned} \mathcal{L}(H) &= \sum_i^N\left(y_i - H(\mathbf{x}_i)\right)^2\\ \mathcal{L}(f_1,f_2,\ldots,f_N) &= \sum_i^N\left(y_i-f_i\right)^2\quad \left(f_i:=H(\mathbf{x}_i)\right) \end{aligned} \end{cases} $$問3
$\mathcal{L}(f_1,f_2,\ldots,f_N)$ と $f_i$ で偏微分した式 $\frac{\partial\mathcal{L}(f_1,f_2,\ldots,f_N)}{f_i}$ を求めよ(これが $\nabla\mathcal{L}$ の成分である)。その式に $f_i = H_{t-1}(\mathbf{x}_i)$ を代入して、次に選択される $h_t$ の条件を
$$\mathbf{x}_i,y_i(1\leq i\leq N),\alpha_{\tau},h_{\tau}(1\leq\tau\leq t-1)$$の式として表せ。
解答
したがって、
$$ \begin{aligned} h_t &= \text{argmax}_h\left|(-\nabla \mathcal{L}) \cdot \frac{h}{\left\|h\right\|}\right|\\ &= \text{argmax}_h\left|\frac{-1}{\|h\|}\sum_i^N-2\left(y_i - \sum_{\tau=1}^{t-1}\alpha_{\tau}h_{\tau}(\mathbf{x}_i)\right)h\left(\mathbf{x}_{i}\right)\right|\\ &= \text{argmax}_h\left|\frac{1}{\|h\|}\sum_i^N\left(y_i - \sum_{\tau=1}^{t-1}\alpha_{\tau}h_{\tau}(\mathbf{x}_i)\right)h\left(\mathbf{x}_{i}\right)\right|\\ \end{aligned} $$問4
問3 の結果を残差 $\hat{y}_i:=y_i - H_{t-1}(\mathbf{x}_i)$ を用いて整理せよ。また、選択の条件を「距離」についてのものに書き換えることで、$L^2$-Boostingが、ほとんど「残差に対する繰り返しの線形回帰」であることを確認せよ。
つまり、この状況では以下の二つの描像はだいたい等価である。
- 訓練データはそのままで、途中の予測器 $H_t$ が更新されていく
- 訓練データ(の教師信号)を更新していった $\hat{y}_i(t)$ に対して $h_t$(と $\alpha_t$)を選ぶ
解答
残差 $\hat{y}_i$ を用いれば、
$$ \begin{aligned} h_t &= \text{argmax}_h\left|\frac{1}{\|h\|}\sum_i^N\left(y_i - \sum_{\tau=1}^{t-1}\alpha_{\tau}h_{\tau}(\mathbf{x}_i)\right)h\left(\mathbf{x}_{i}\right)\right|\\ &= \text{argmax}_h\left|\frac{1}{\|h\|}\sum_i^N\hat{y}_ih(\mathbf{x}_i)\right|\\ \end{aligned} $$と整理できる。また、選択の条件を「距離」についてのものに書き換えると、 $$ \begin{aligned} h_t &= \text{argmax}_h\left|(-\nabla \mathcal{L}) \cdot \frac{h}{\left\|h\right\|}\right|\\ &= \text{argmin}_h\left\|(-\nabla \mathcal{L}) - \frac{h}{\left\|h\right\|}\right\|\qquad \left(\because \text{$\frac{h}{\left\|h\right\|}$ is const.}\right)\\ &= \text{argmin}_h\sqrt{\sum_{i=1}^N\left(2\left(y_i - \sum_{\tau=1}^{t-1}\alpha_{\tau}h_{\tau}(\mathbf{x}_i)\right) - \frac{h(\mathbf{x}_i)}{\left\|h\right\|} \right)^2}\\ &= \text{argmin}_h\sum_{i=1}^N\left(2\hat{y}_i - \frac{h(\mathbf{x}_i)}{\left\|h\right\|} \right)^2\\ \end{aligned} $$
よって、ほとんど「残差に対する繰り返しの線形回帰」であることが確認できた。
解答
ここで、$\hat{y}_i$ は $\alpha_t$ に依存していないので、
$$ \begin{aligned} \frac{\partial\left(\Delta\mathcal{L}\right)}{\partial\alpha_t} &= \sum_{i=1}^N2\alpha_th_t^2(\mathbf{x}_i) - 2h_t(\mathbf{x}_i)\hat{y}_i = 0\\ \therefore \alpha_t&=\frac{\sum_{i=1}^Nh_t(\mathbf{x}_i)\hat{y}_i}{\sum_{i=1}^Nh_t^2(\mathbf{x}_i)} \\ &= \frac{1}{\|h_t\|^2}\sum_{i=1}^Nh_t(\mathbf{x}_i)\hat{y}_i\\ \end{aligned} $$をとる時変化分 $\Delta\mathcal{L}$ は最大となる。また、この時 $\Delta\mathcal{L}$ の値は、
$$ \begin{aligned} \Delta\mathcal{L}\left(\alpha_t\right) &= \alpha_t\left(\alpha_t\sum_{i=1}^Nh_t^2(\mathbf{x}_i) - \sum_{i=1}^N 2h_t(\mathbf{x}_i)\hat{y}_i\right)\\ &= \alpha_t\left(\sum_{i=1}^Nh_t(\mathbf{x}_i)\hat{y}_i - \sum_{i=1}^N 2h_t(\mathbf{x}_i)\hat{y}_i\right)\\ &= - \alpha_t\sum_{i=1}^N h_t(\mathbf{x}_i)\hat{y}_i\\ &= - \left(\frac{1}{\|h_t\|}\sum_{i=1}^Nh_t(\mathbf{x}_i)\hat{y}_i\right)^2 \end{aligned} $$となる。これは、問3 の結果を残差 $\hat{y}_i:=y_i - H_{t-1}(\mathbf{x}_i)$ を用いて整理した結果と等しい。
演習
$L^2$-Boostingを使ってKaggle のデータセット King County の住宅価格を予測してみる。[https://www.kaggle.com/harlfoxem/housesalesprediction](https://www.kaggle.com/harlfoxem/housesalesprediction) からCSVのデータセットを取得して、`price` を説明するモデルを学習する。k-fold cross validation を実施してテストデータに対する性能を単純な線形回帰のモデルと比較する。import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("kc_house_data.csv")
df.head(3)
単純な線形モデルの構築¶
以下の形で表される最も簡単なモデルを構築する。なお、このとき最も相関が強い特徴量 $x$ を選択する。
$$h_{\theta}(x) = \theta_0 + \theta_1x$$df.corr().loc["price"].sort_values(ascending=False)
sqft_living が最も price と相関が強いことがわかる。そこで、sqft_living を用いて最も簡単なモデルを作成して、関係性をプロットする。
from kerasy.ML.linear import LinearRegression
from kerasy.utils import root_mean_squared_error, train_test_split
y = df["price"].values.reshape(-1,1)
x = df["sqft_living"].values.reshape(-1,1)
(x_train,x_test),(y_train,y_test) = train_test_split(x,y,train_size = 0.8,random_state=0)
simple_lr = LinearRegression()
simple_lr.fit(x_train, y_train)
y_pred = simple_lr.predict(x_test)
rmse = root_mean_squared_error(y_pred, y_test)
intercept, coef = simple_lr.w[:,0]
print(f"Average Price for Test Data : {y_test.mean()}")
print(f"Root Mean Squared Error (RMSE): {rmse[0]}")
print(f"Intercept (theta_0) : {intercept}")
print(f"Coefficient (theta_1) : {coef}")
plt.figure(figsize=(8,6))
plt.scatter(x_test,y_test,color='darkgreen',label="Data", alpha=.1)
plt.plot(x_test,y_pred,color="red",label="Predicted Regression Line")
plt.xlabel("Living Space (sqft)", fontsize=15)
plt.ylabel("Price ($)", fontsize=15)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
plt.legend()
plt.show()
この図より、sqft_living だけでもある程度の予測ができていることがわかる。
各種特徴量の可視化¶
remove_cols = ['id', 'date']
feature_columns = [col for col in df.columns if col not in remove_cols]
print(feature_columns)
hist = df[feature_columns].hist(bins=25,figsize=(16,16),xlabelsize='10',ylabelsize='10',xrot=-15)
[x.title.set_size(18) for x in hist.ravel()]
plt.tight_layout()
plt.show()
ここで、離散的な特徴量と連続的な特徴量があることが見て取れる。全てを可視化することはしないが、それぞれ objVSexp で可視化が可能である。
from kerasy.utils import objVSexp
fig = plt.figure(figsize=(18,4))
# 離散値
ax1 = fig.add_subplot(1,3,1)
ax1 = objVSexp(df["price"], df["grade"], var_type="discrete", ax=ax1)
ax1.set(xlabel='Grade', ylabel='Price')
# 連続値(2次元)
ax2 = fig.add_subplot(1,3,2)
ax2 = objVSexp(df["price"], df["sqft_living"], var_type="continuous", ax=ax2)
ax2.set(xlabel='sqft Living', ylabel='Price')
# 連続値(3次元)
ax3 = fig.add_subplot(1,3,3,projection="3d")
ax3 = objVSexp(df["bedrooms"], df['sqft_living'],df['sqft_lot'], var_type="continuous", ax=ax3)
ax3.set(xlabel='\n sqft Living',ylabel='\nsqft Lot',zlabel='Bedrooms', ylim=[0,250000])
plt.tight_layout()
plt.show()
特徴量の追加¶
date, yr_built, yr_renovatedから、より意味のある特徴量 age(築年数), age_rnv(改築年数)を作成する。
df['sales_yr'] = df['date'].astype(str).str[:4].astype(int)
df["age"] = df['sales_yr'] - df['yr_built']
df['age_rnv'] = df.apply(lambda x: x.sales_yr-x.yr_renovated if x.yr_renovated!=0 else 0, axis=1)
ax = objVSexp(df["price"], df["age"], var_type="discrete")
plt.show()
このままでは利用しづらいので、Binningを行う。
bins = [-2,0,5,10,25,50,75,100,100000]
labels = ['<1','1-5','6-10','11-25','26-50','51-75','76-100','>100']
df['age_binned'] = pd.cut(df['age'], bins=bins, labels=labels)
age_rank = np.arange(len(labels))
age_encoder = dict(zip(labels, age_rank))
fig = plt.figure(figsize=(12,4))
ax1 = fig.add_subplot(1,2,1)
ax1 = objVSexp(df["price"], df["age_binned"], var_type="discrete", ax=ax1)
ax1.set_title("Age", fontsize=18)
ax2 = fig.add_subplot(1,2,2)
ax2 = objVSexp(df["price"], df["sales_yr"], var_type="discrete", ax=ax2)
ax2.set_title("Sales Year", fontsize=18)
plt.tight_layout()
plt.show()
意外なことに、築年数だけでは価格を予測できそうになかった。
線形回帰¶
df["age_binned"] = df["age_binned"].apply(lambda x:age_encoder[x])
remove_cols = ['id', 'date', 'age', 'yr_built', 'yr_renovated', 'zipcode']
feature_columns = [col for col in df.columns if col not in remove_cols]
Ycol = "price"
Xcols = [col for col in feature_columns if col != Ycol]
print(Xcols)
X = df[Xcols].values
Y = df[Ycol].values.reshape(-1,1)
(X_train,X_test),(Y_train,Y_test) = train_test_split(X,Y,train_size=0.8,random_state=0)
from kerasy.utils import cross_validation
k_fold_seed = 134
単純な線形回帰のモデル¶
全ての特徴量について線形に足し合わせるた単純なモデルを考える。
$$h_{\theta}(\mathbf{x}) = \theta_0 + \theta_1x_1 + \cdots + \theta_Mx_M$$modelkwargs = {
"basis": "none",
"add_bias": True,
}
score = cross_validation(
k=5, x=X_train, y=Y_train,
metrics=root_mean_squared_error,
seed=k_fold_seed,
modelcls=LinearRegression,
modelkwargs=modelkwargs
)
lr = LinearRegression(**modelkwargs)
lr.fit(X_train, Y_train)
Y_pred = lr.predict(X_test)
max_val = max(np.concatenate([Y_pred,Y_test]))[0]
plt.figure(figsize=(8,6))
plt.scatter(Y_pred,Y_test,color='darkgreen',label="Data", alpha=.1)
plt.plot((0,max_val), (0,max_val), color="red")
plt.xlabel("Predicted", fontsize=15), plt.ylabel("Answer", fontsize=15)
plt.xticks(fontsize=13), plt.yticks(fontsize=13), plt.title(f"Simple Linear Regression (k-fold RMSE={score[0]:.3f})")
plt.legend()
plt.show()
多項式の特徴量を追加した線形回帰のモデル¶
続いて、全ての特徴量について、多項式の影響も考えたモデルを考える。ここでは、$K=3$ で考える。
$$h_{\theta}(\mathbf{x}) = \theta_0 + \left(\theta_{1,1}x_1 +\cdots+ \theta_{1,K}x_1^K\right) + \cdots + \left(\theta_{M,1}x_M +\cdots+ \theta_{M,K}x_M^K\right)$$modelkwargs={
"basis": "polynomial",
"add_bias": True,
"exponent": np.arange(1,4)
}
score = cross_validation(
k=5, x=X_train, y=Y_train,
metrics=root_mean_squared_error, seed=k_fold_seed,
modelcls=LinearRegression,
modelkwargs = modelkwargs
)
lr = LinearRegression(**modelkwargs)
lr.fit(X_train, Y_train)
Y_pred = lr.predict(X_test)
max_val = max(np.concatenate([Y_pred,Y_test]))[0]
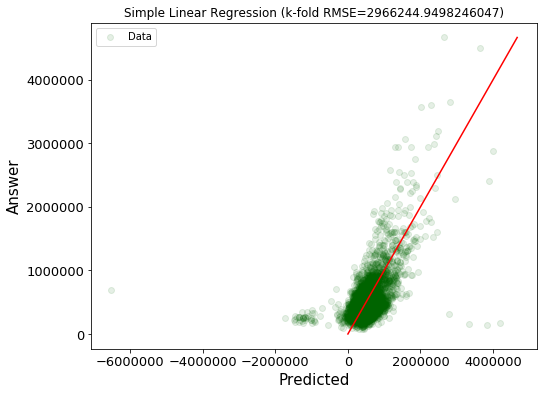
plt.figure(figsize=(8,6))
plt.scatter(Y_pred,Y_test,color='darkgreen',label="Data", alpha=.1)
plt.plot((0,max_val), (0,max_val), color="red")
plt.xlabel("Predicted", fontsize=15), plt.ylabel("Answer", fontsize=15)
plt.xticks(fontsize=13), plt.yticks(fontsize=13), plt.title(f"Simple Linear Regression (k-fold RMSE={score[0]})")
plt.legend()
plt.show()
Boosting Algorithm¶
from kerasy.ML.boosting import L2Boosting
num_iteration = 30
num_elements = 20
max_num_feature = 3
boosting_seed = 0
N,D = X_train.shape
idxes = np.arange(D)
features = np.asarray(Xcols)
import itertools
AllModelComb = []
for num_feature in range(1, max_num_feature+1):
AllModelComb += list(itertools.combinations(idxes, num_feature))
selected_idxes = np.random.RandomState(boosting_seed).choice(AllModelComb, num_elements, replace=False)
Models = []
Masks = np.zeros(shape=(0,D), dtype=bool)
print(f"{'id':^{len(str(num_elements))}}: features")
print("-"*30)
for i,idxcomb in enumerate(selected_idxes):
idxes = np.asarray(idxcomb)
mask = np.zeros(shape=(D,), dtype=bool)
mask[idxes] = 1
X = X_train[:,mask]
# Weak Learners
lr = LinearRegression("polynomial", exponent=1)
lr.fit(X, Y_train)
Models.append(lr)
Masks = np.r_[Masks, mask.reshape(1,D)]
print(f"{i:>0{len(str(num_elements))}}: {', '.join(features[mask])}")
上記の特徴量を用いたモデルが作成できたので、これらを用いてBoostingを行う。
modelkwargs={
"Models": Models,
"Masks": Masks,
}
trainkwargs={
"T": num_iteration
}
score = cross_validation(
k=5, x=X_train, y=Y_train,
metrics=root_mean_squared_error,
seed=k_fold_seed,
modelcls=L2Boosting,
modelkwargs=modelkwargs,
trainkwargs=trainkwargs
)
boosting = L2Boosting(**modelkwargs)
boosting.fit(X_train, Y_train, **trainkwargs)
Y_pred = boosting.predict(X_test)
max_val = max(np.concatenate([Y_pred,Y_test]))[0]
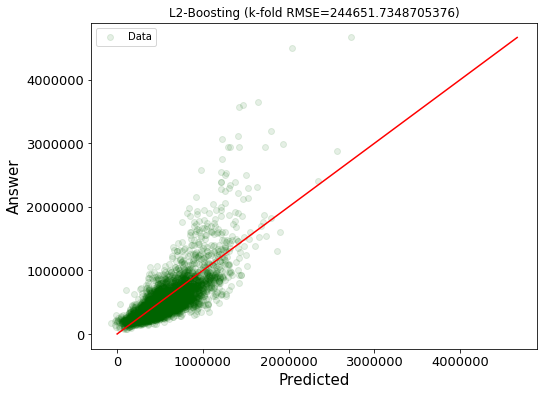
plt.figure(figsize=(8,6))
plt.scatter(Y_pred,Y_test,color='darkgreen',label="Data", alpha=.1)
plt.plot((0,max_val), (0,max_val), color="red")
plt.xlabel("Predicted", fontsize=15), plt.ylabel("Answer", fontsize=15)
plt.xticks(fontsize=13), plt.yticks(fontsize=13), plt.title(f"L2-Boosting (k-fold RMSE={score[0]})")
plt.legend()
plt.show()
| 単純な線形回帰のモデル | 多項式の特徴量を追加した線形回帰のモデル | Boosting Algorithm | |
|---|---|---|---|
| RMSE | 210,425 | 2,966,244 | 244,652 |
| プロット | 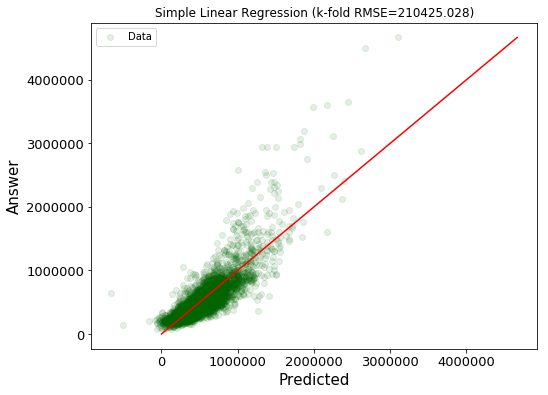 |
 |
 |