CNN
Notebook
Example Notebook: Kerasy.examples.MNIST.ipynb
CNN is originated from Neocognitron, which was devised based on the neurophysiological knowledge (visual cortex of the living organism's brain), and has a structure specialized for image processing.
Neocognitron consists of:
- Convolutional Layer : corresponding to simple cells (S-cells) for feature extraction
- Pooling Layer : corresponding to complex cells (C-cells) having a function of allowing positional deviation.
CNN can learn well by using backpropagation. The algorithm is shown mathematically below.
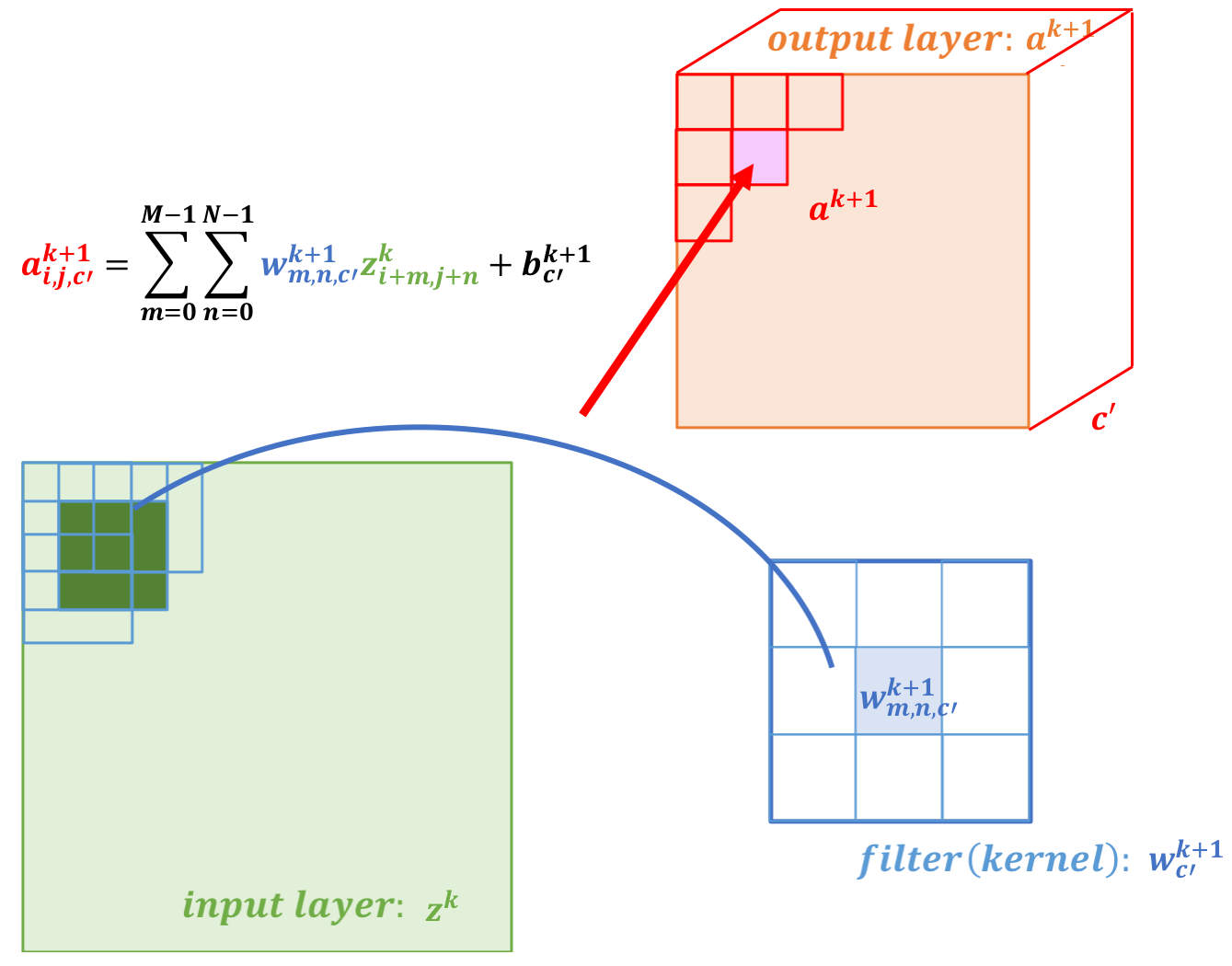
Convolutional Layer
| Mono | Multi |
|---|---|
 |
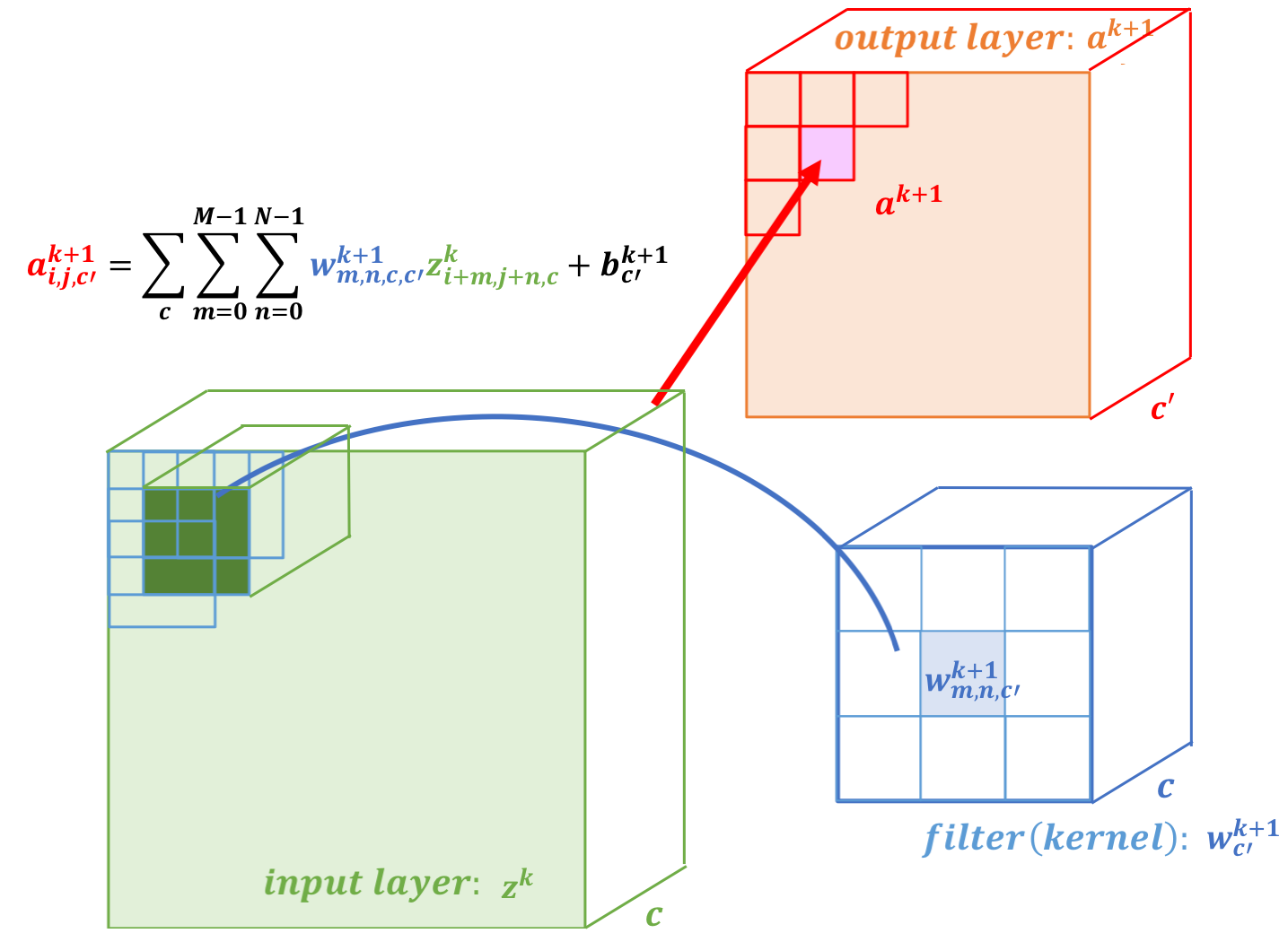 |
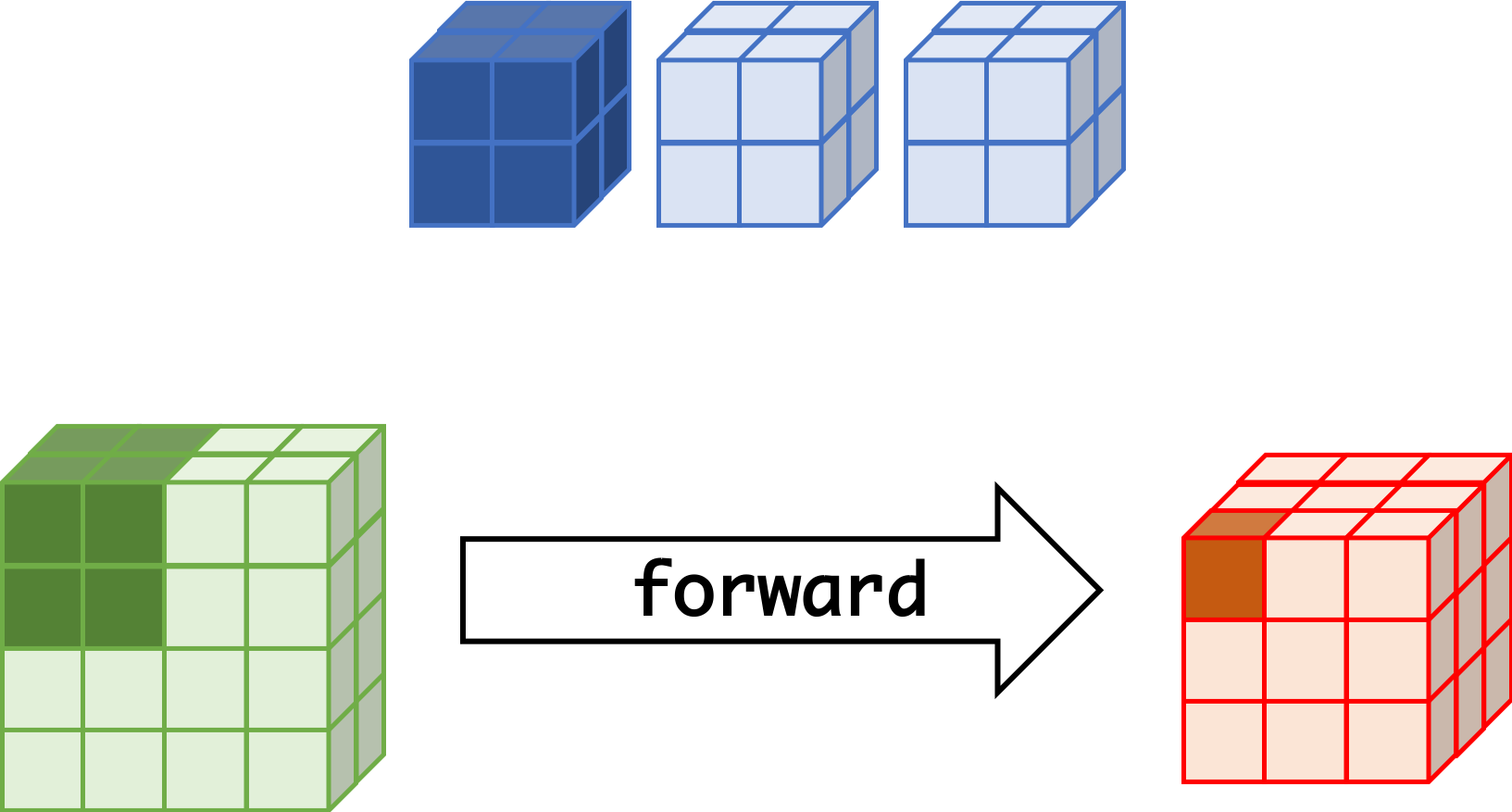
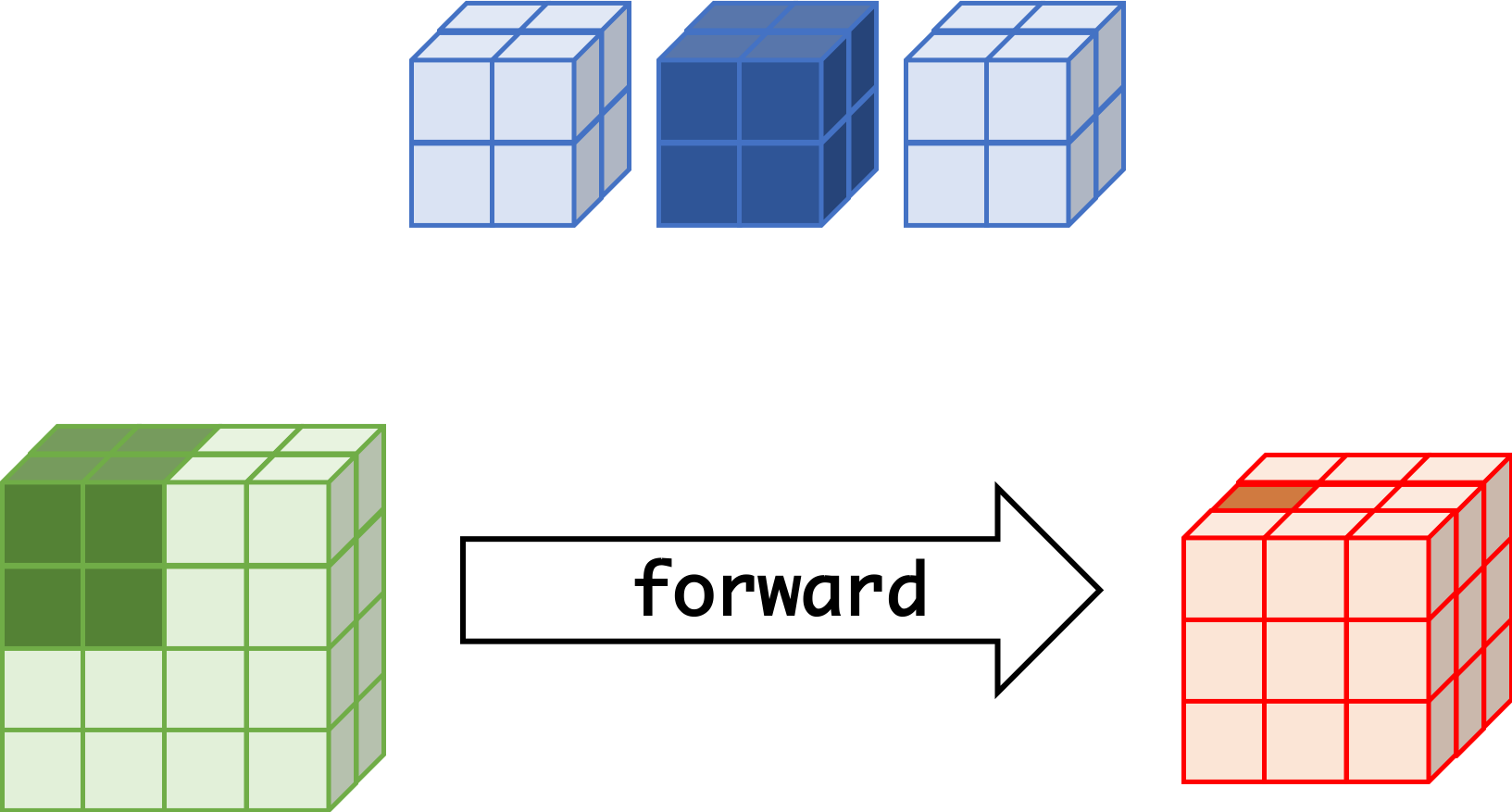
forward¶
 |
 |
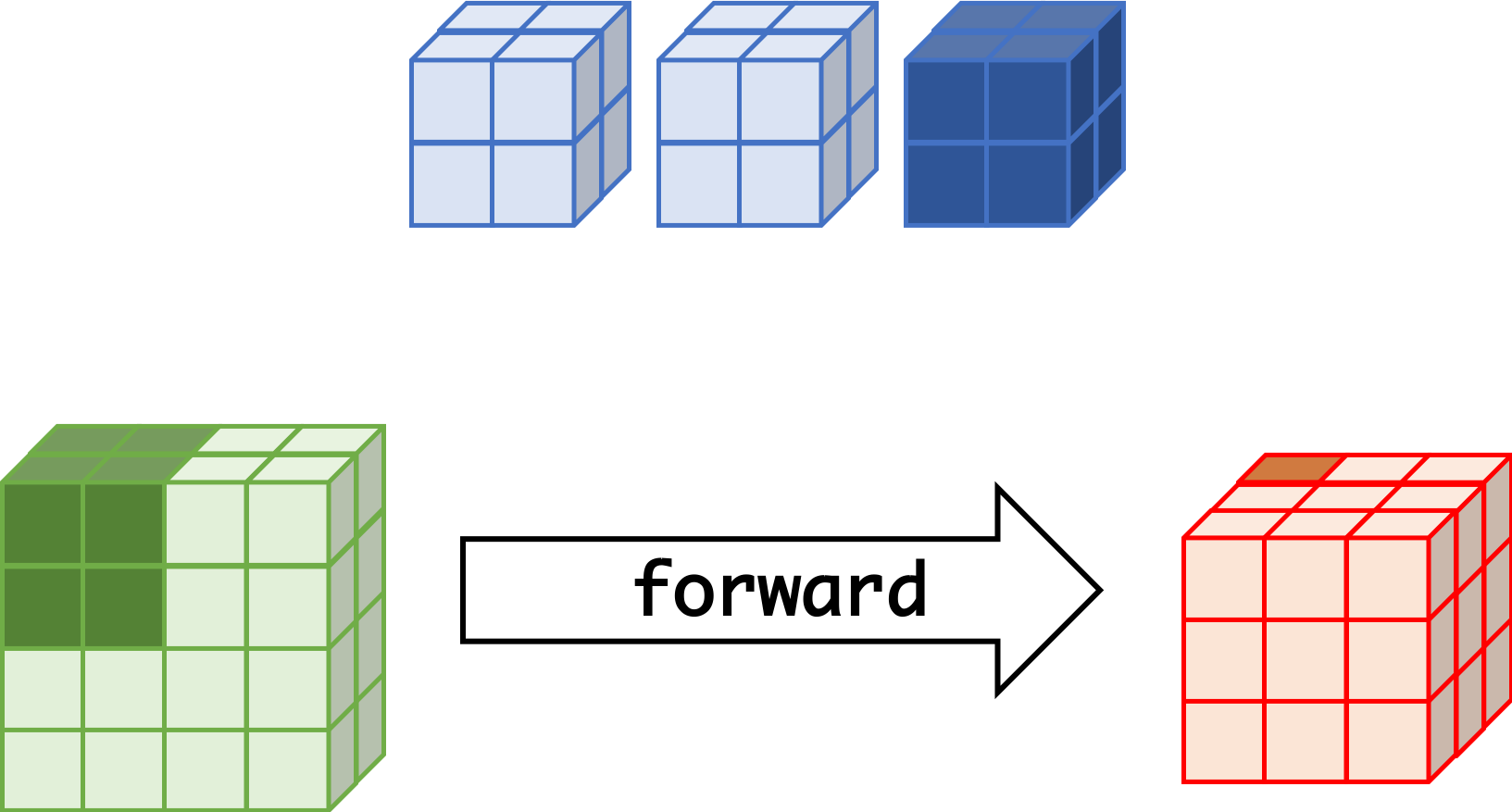 |
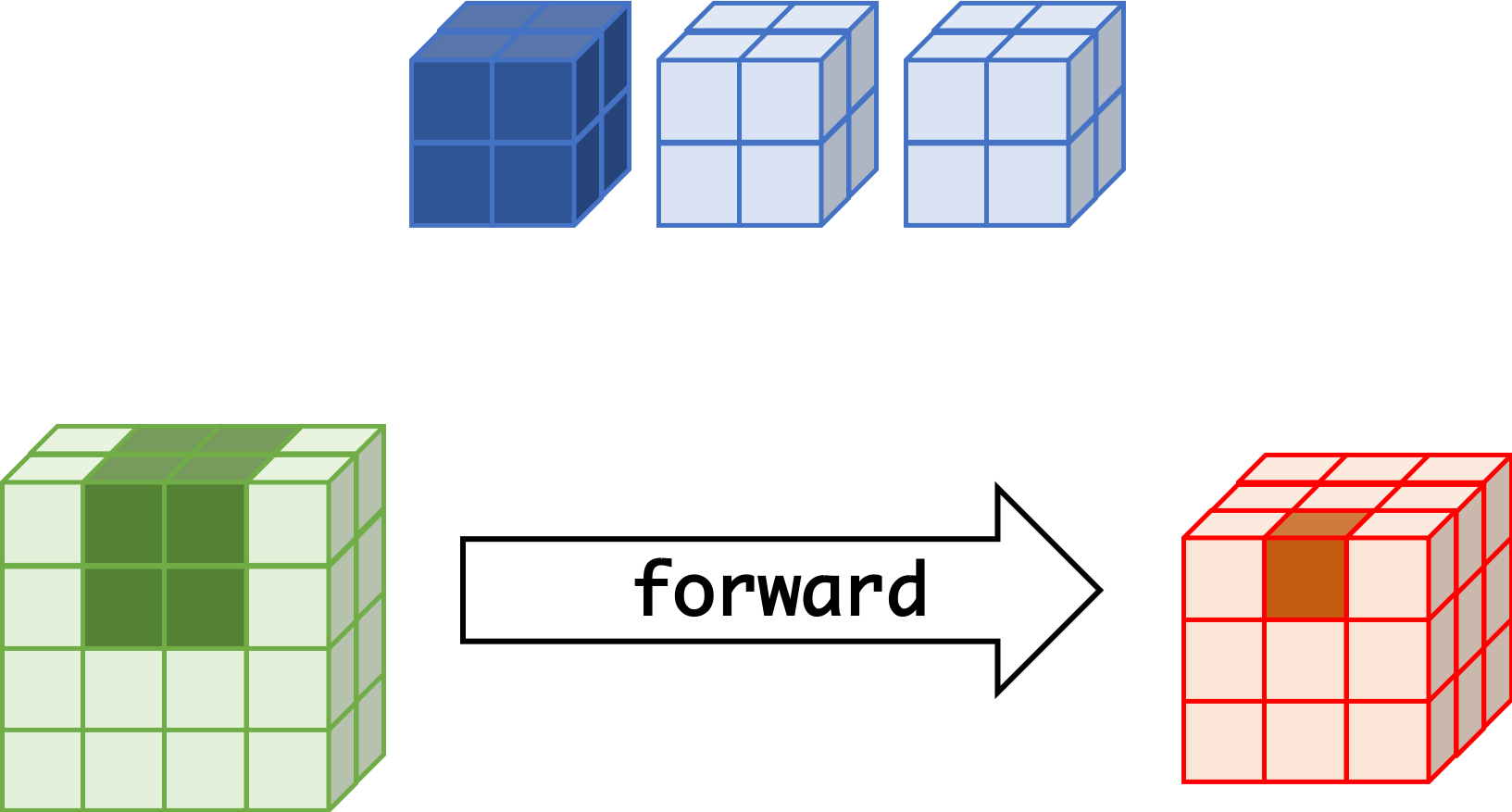 |
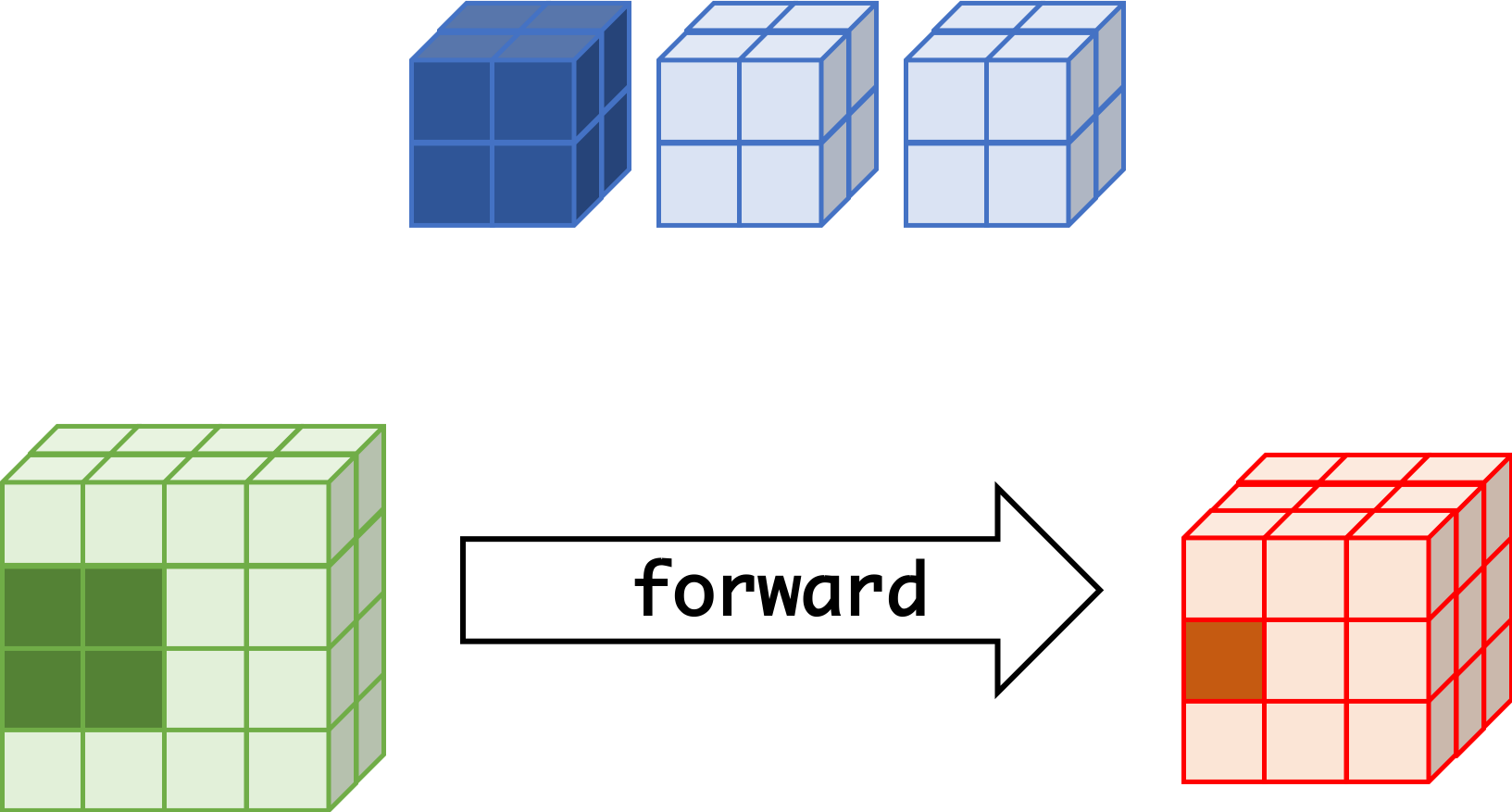 |
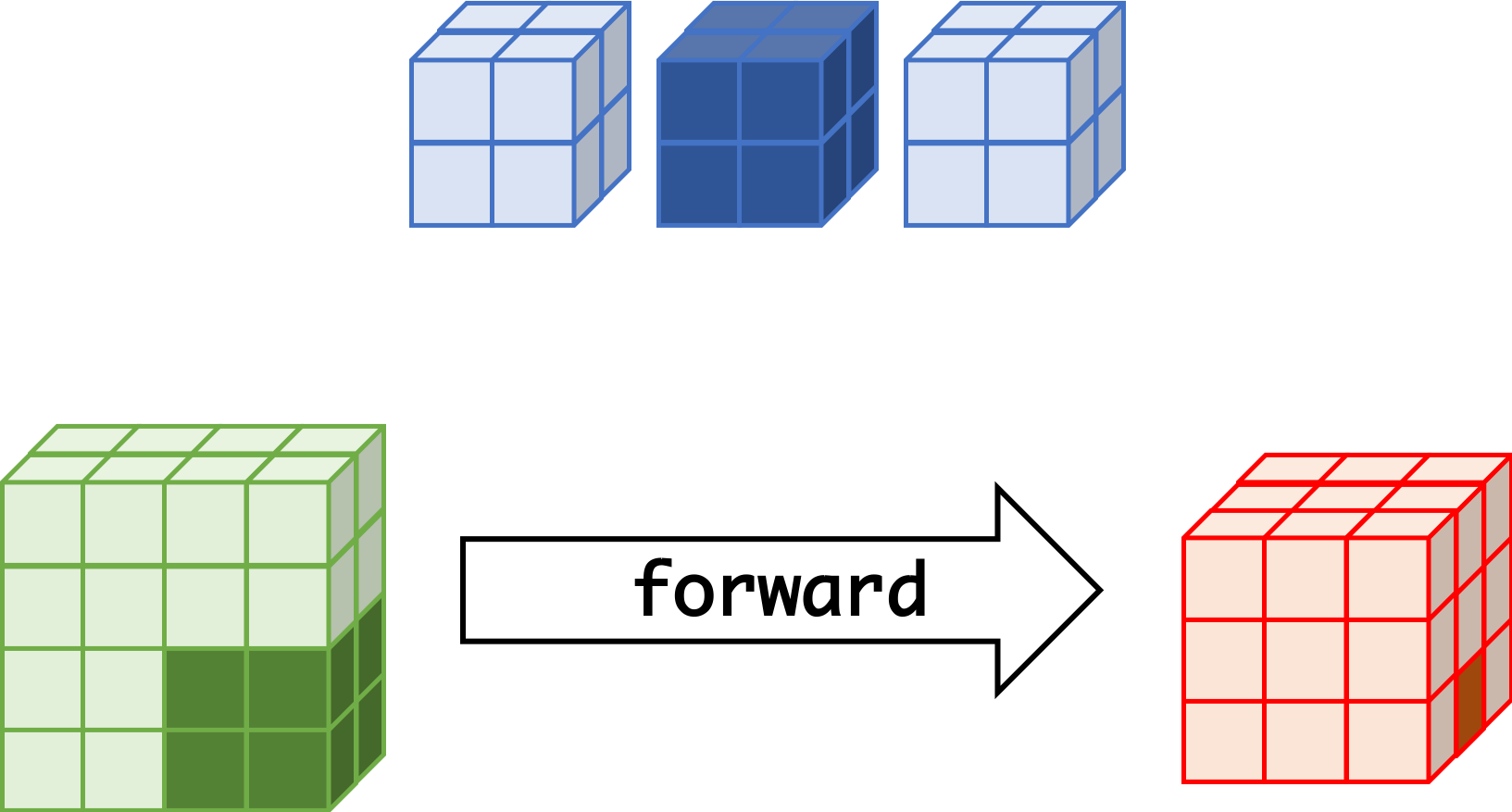 |
backprop¶
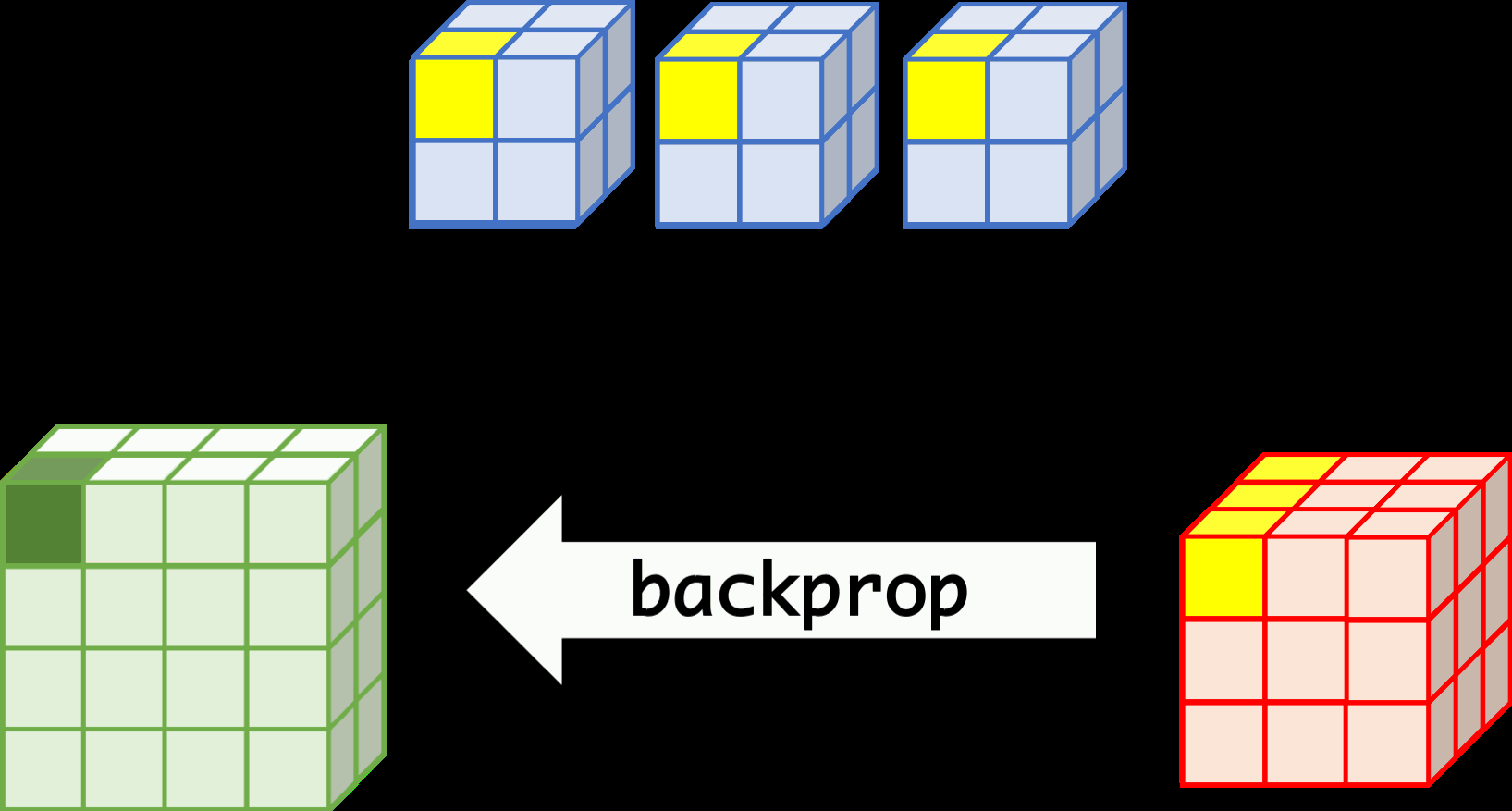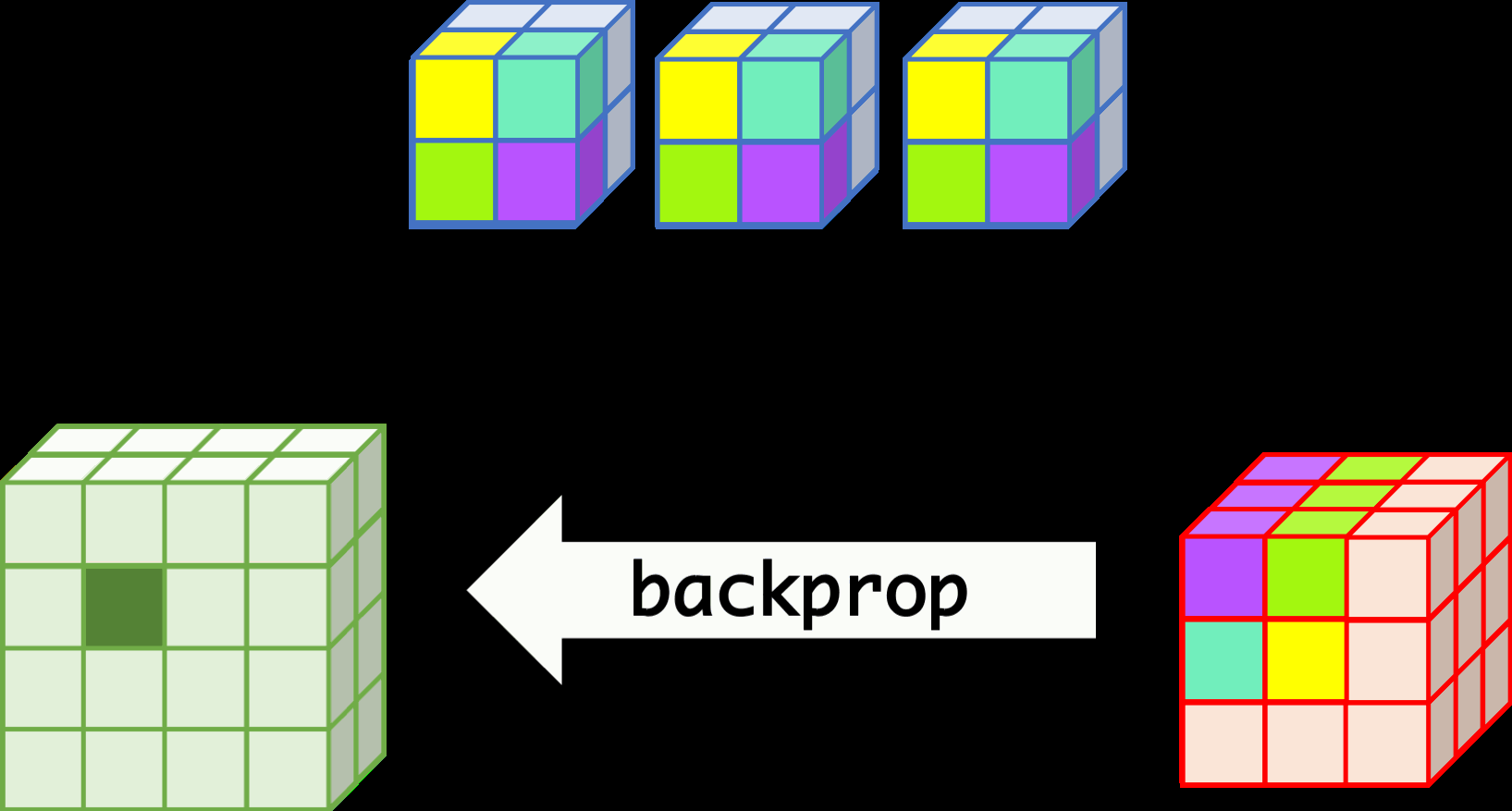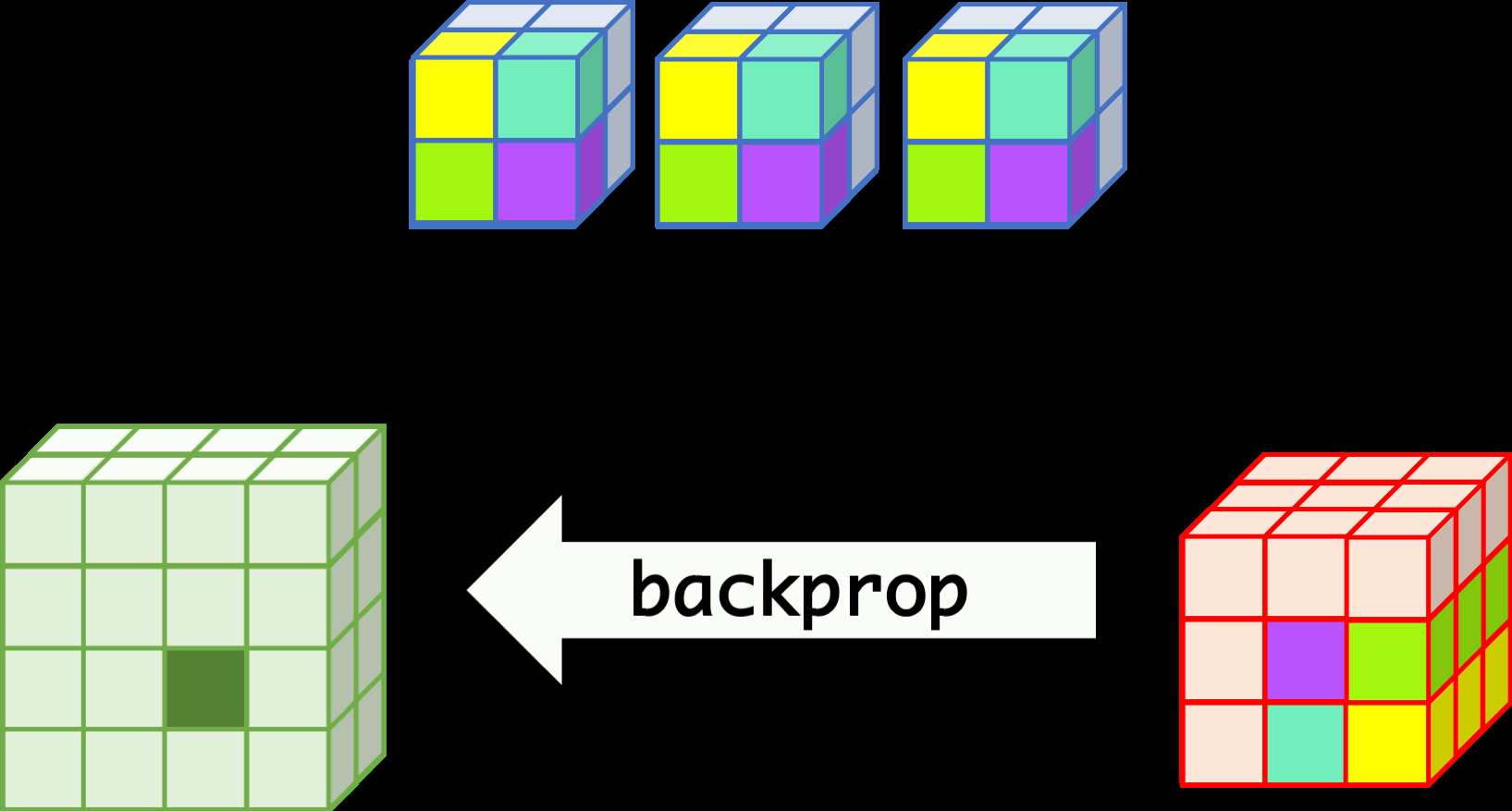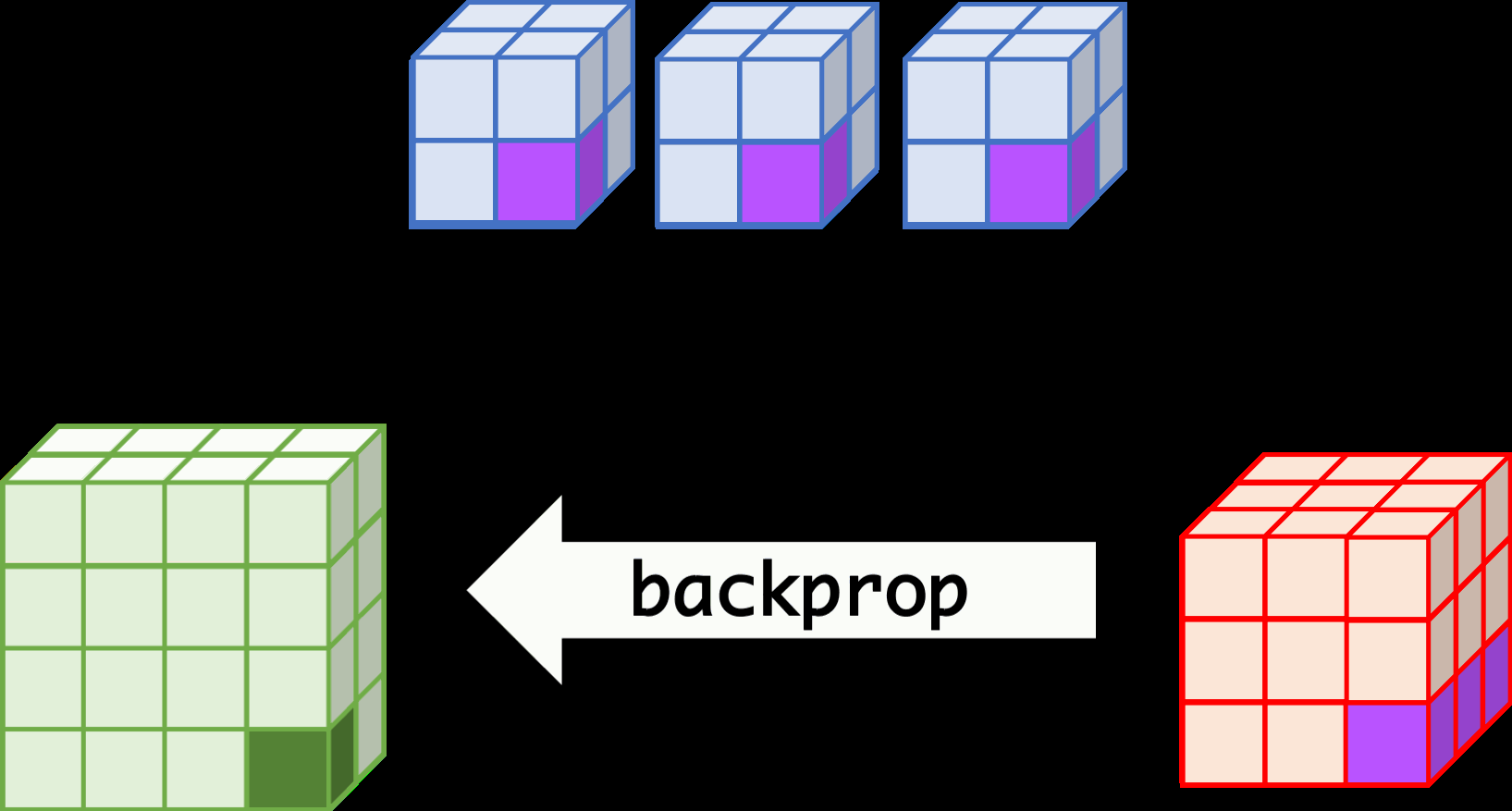
Check image individually
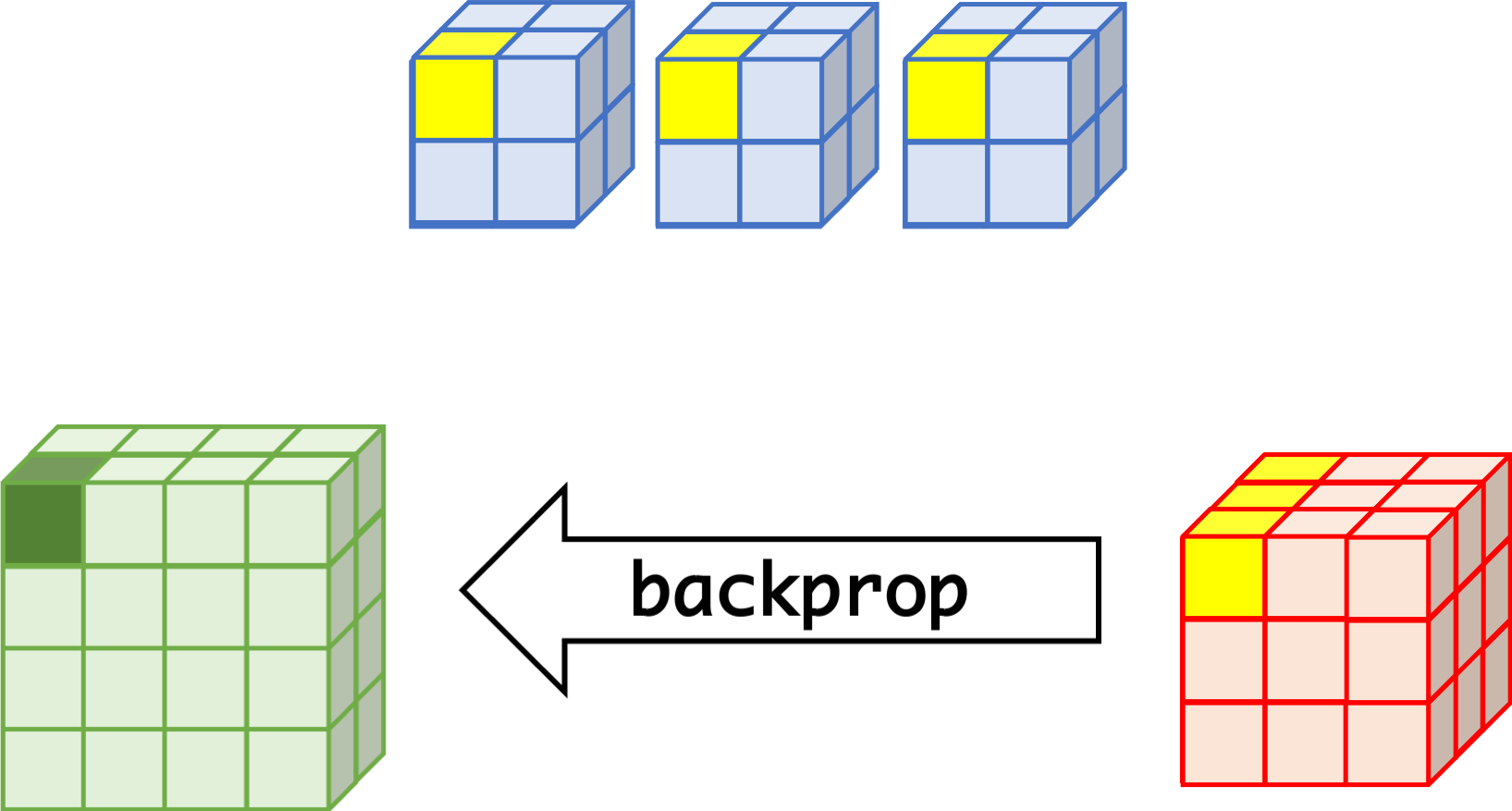 |
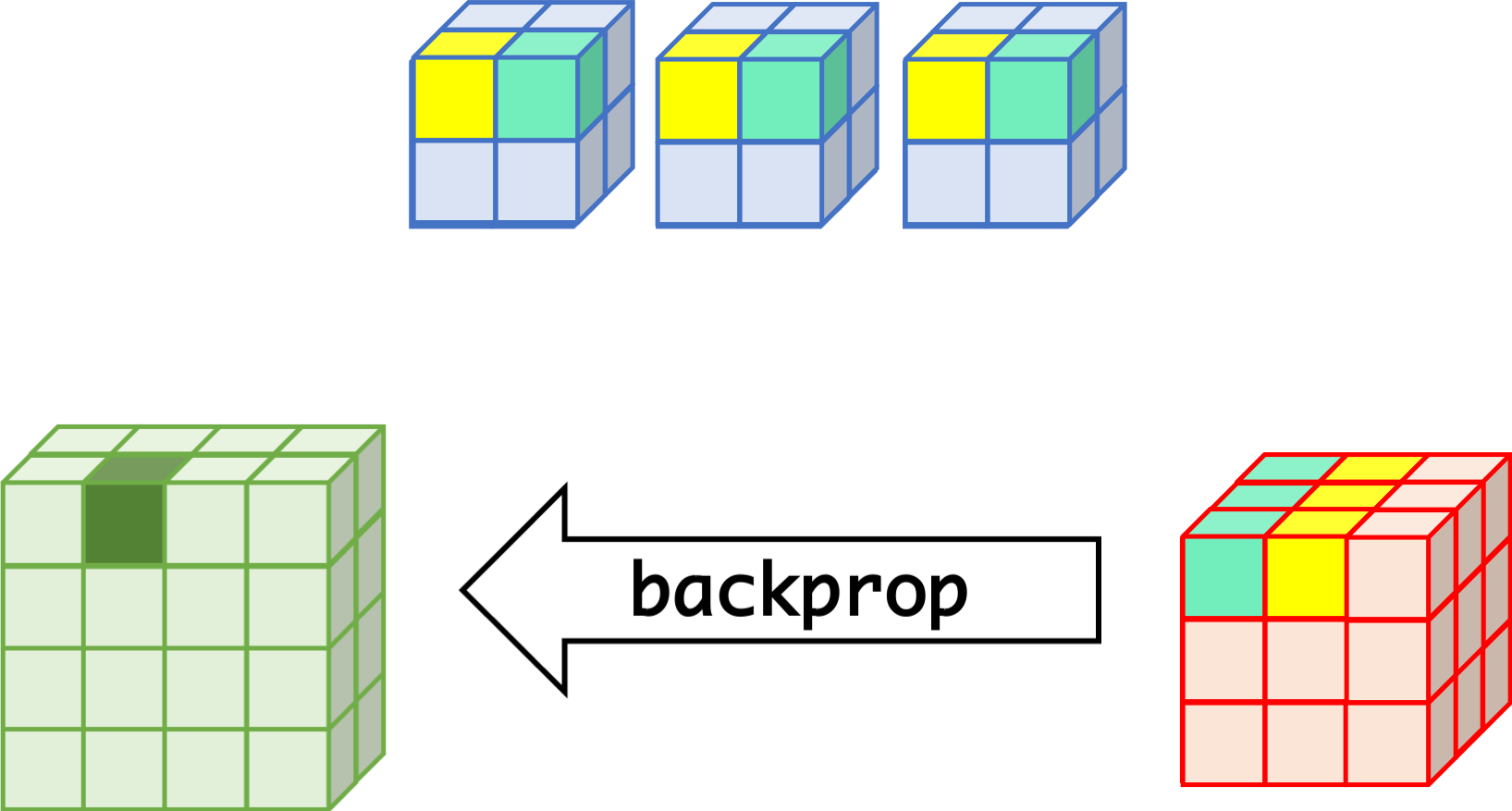 |
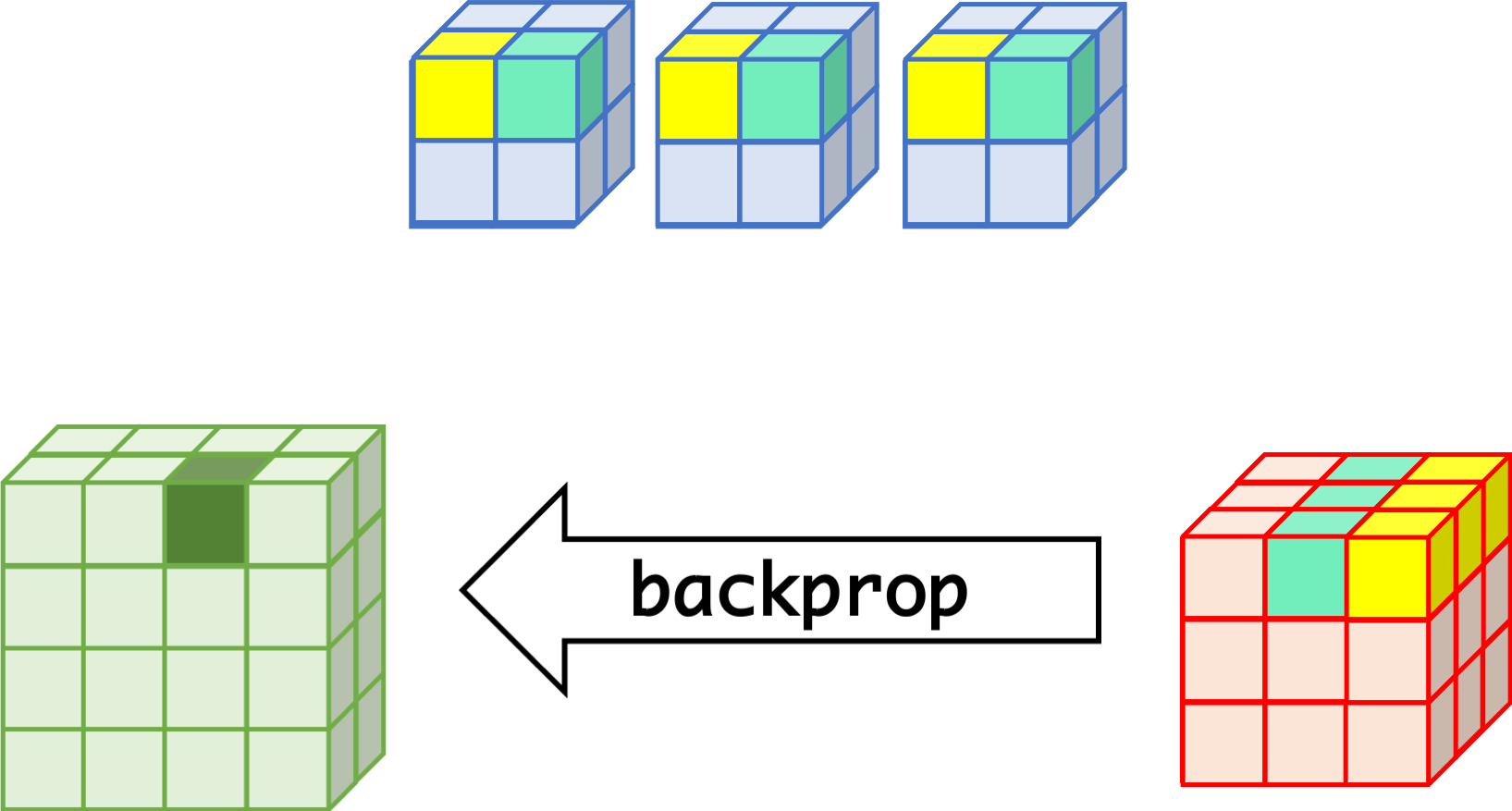 |
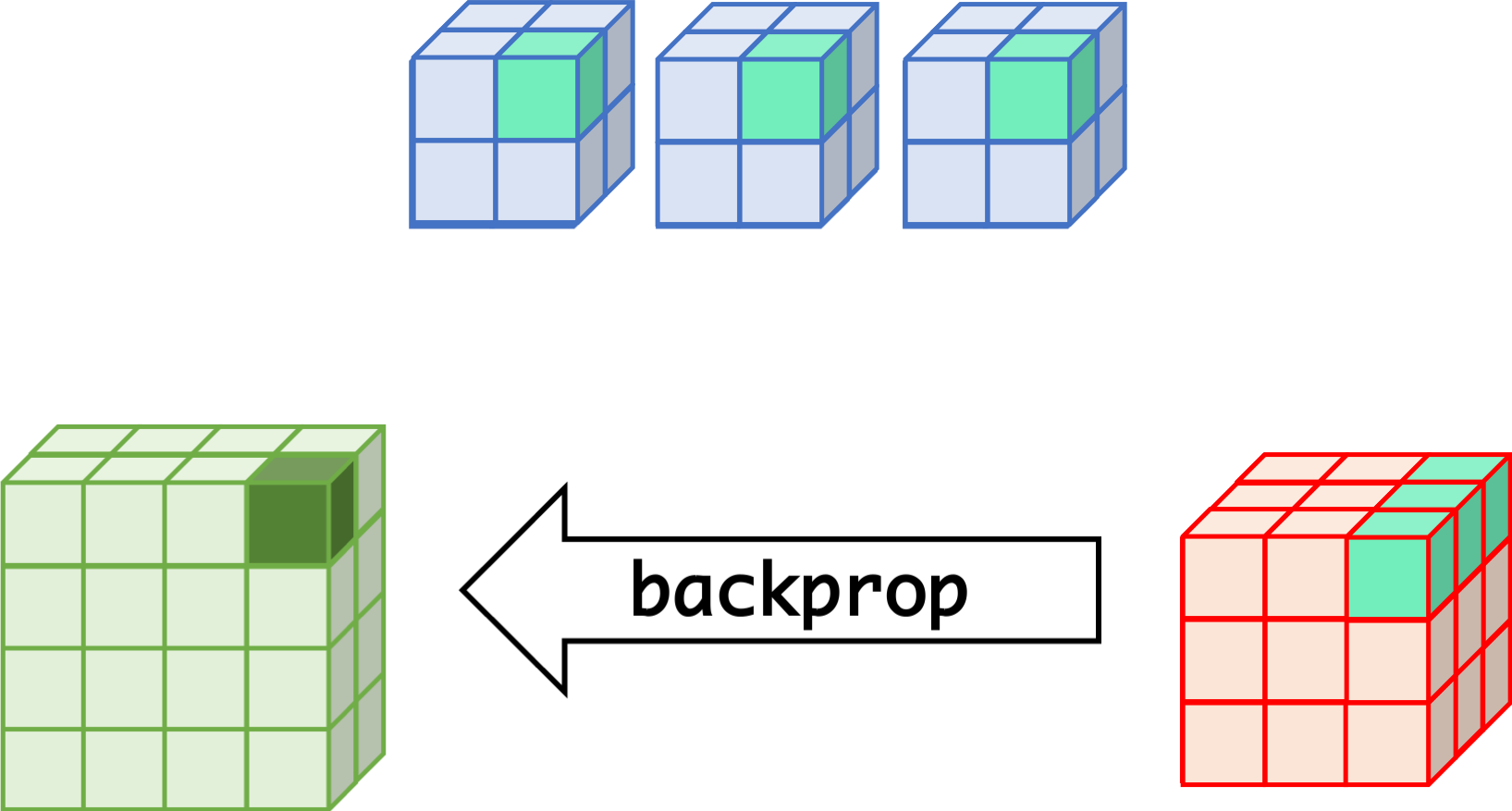 |
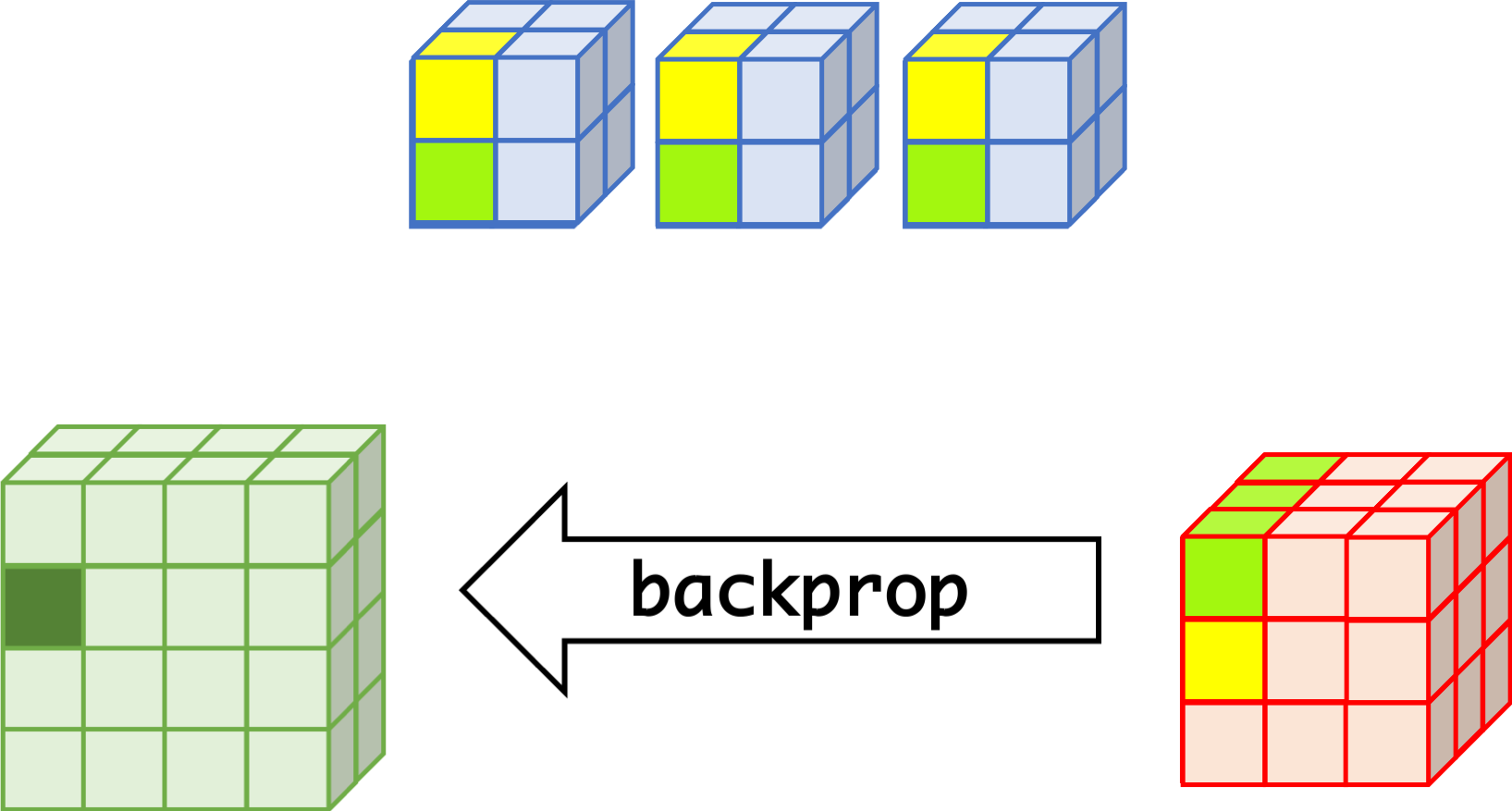 |
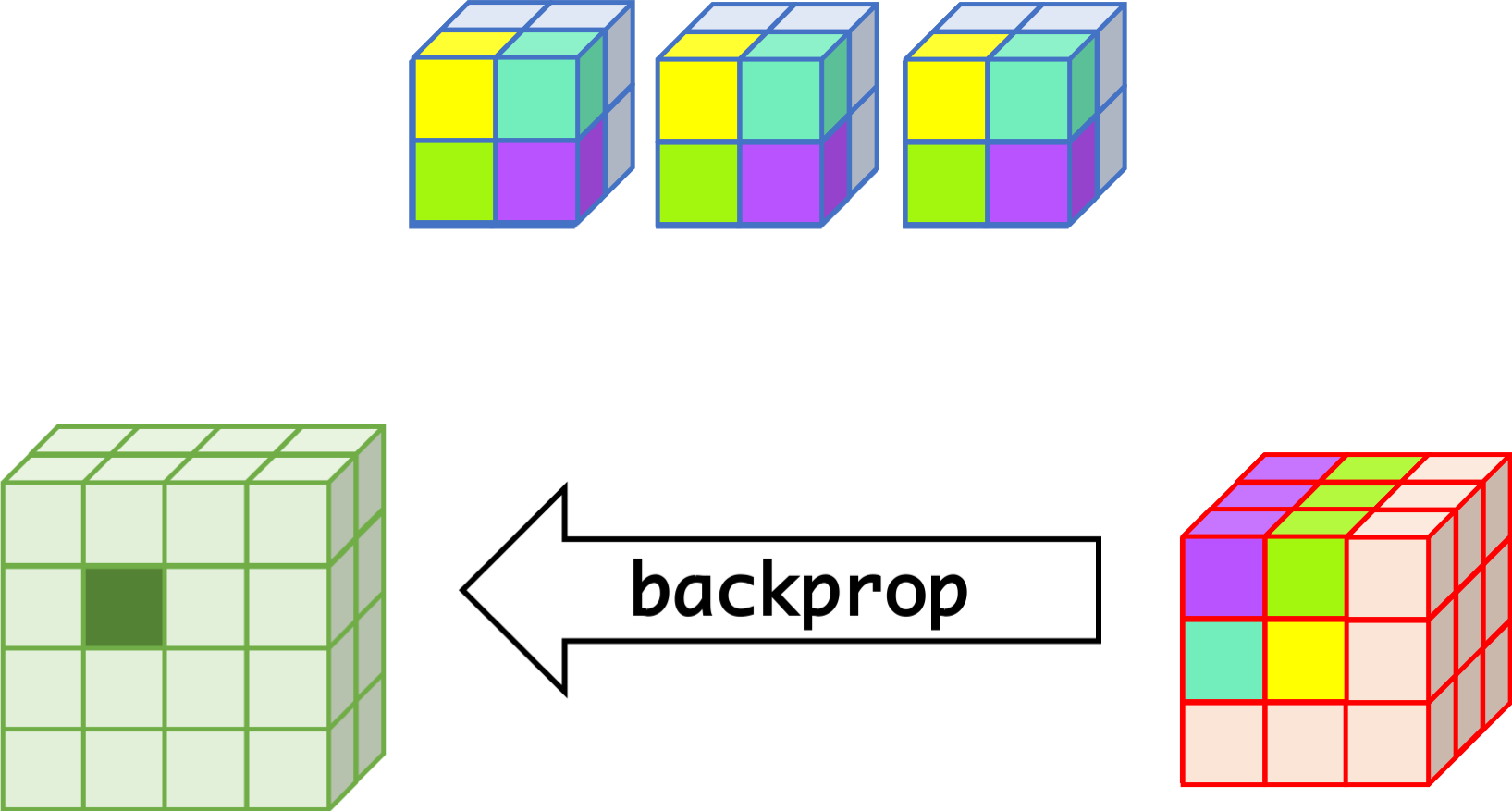 |
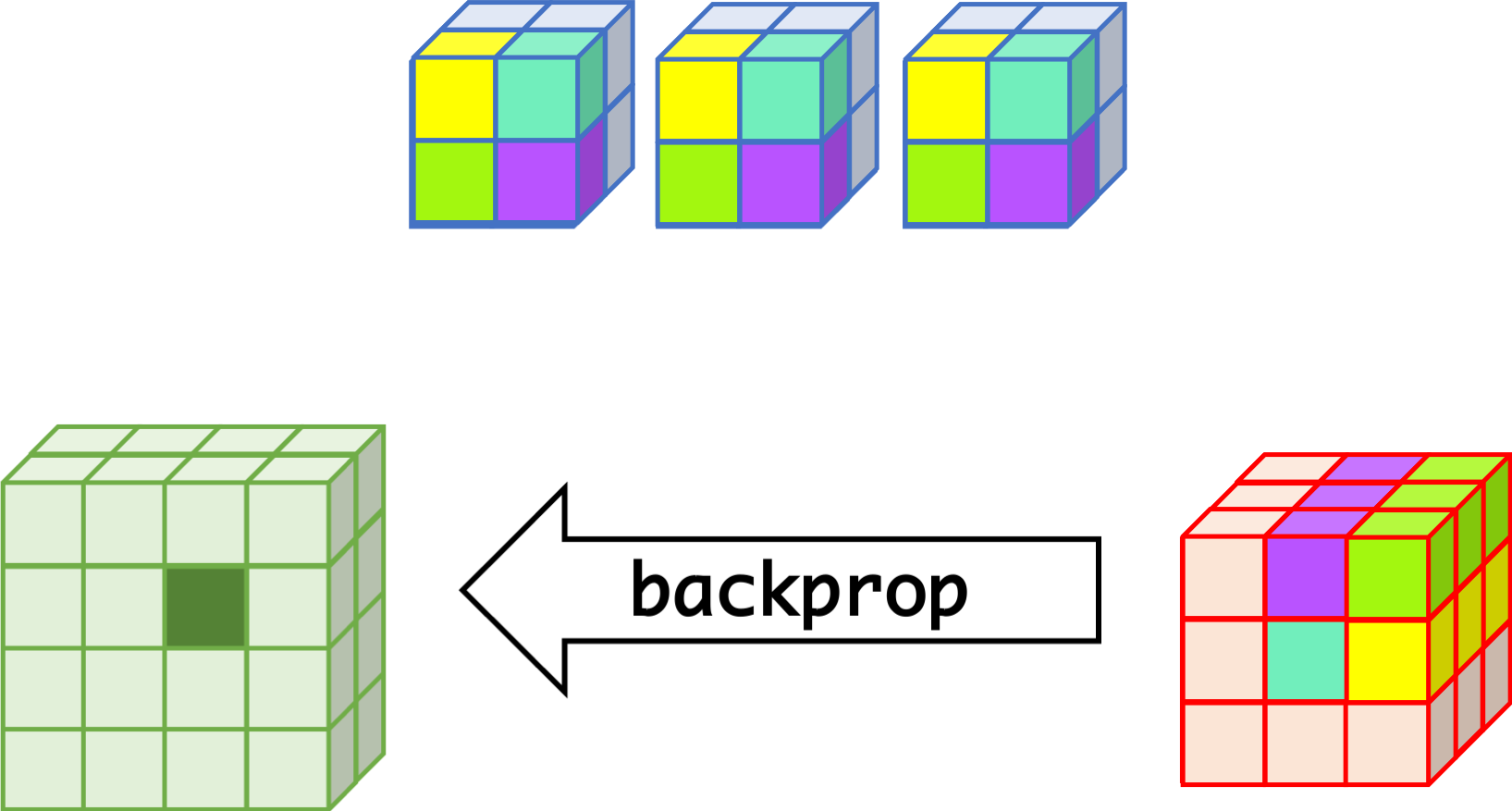 |
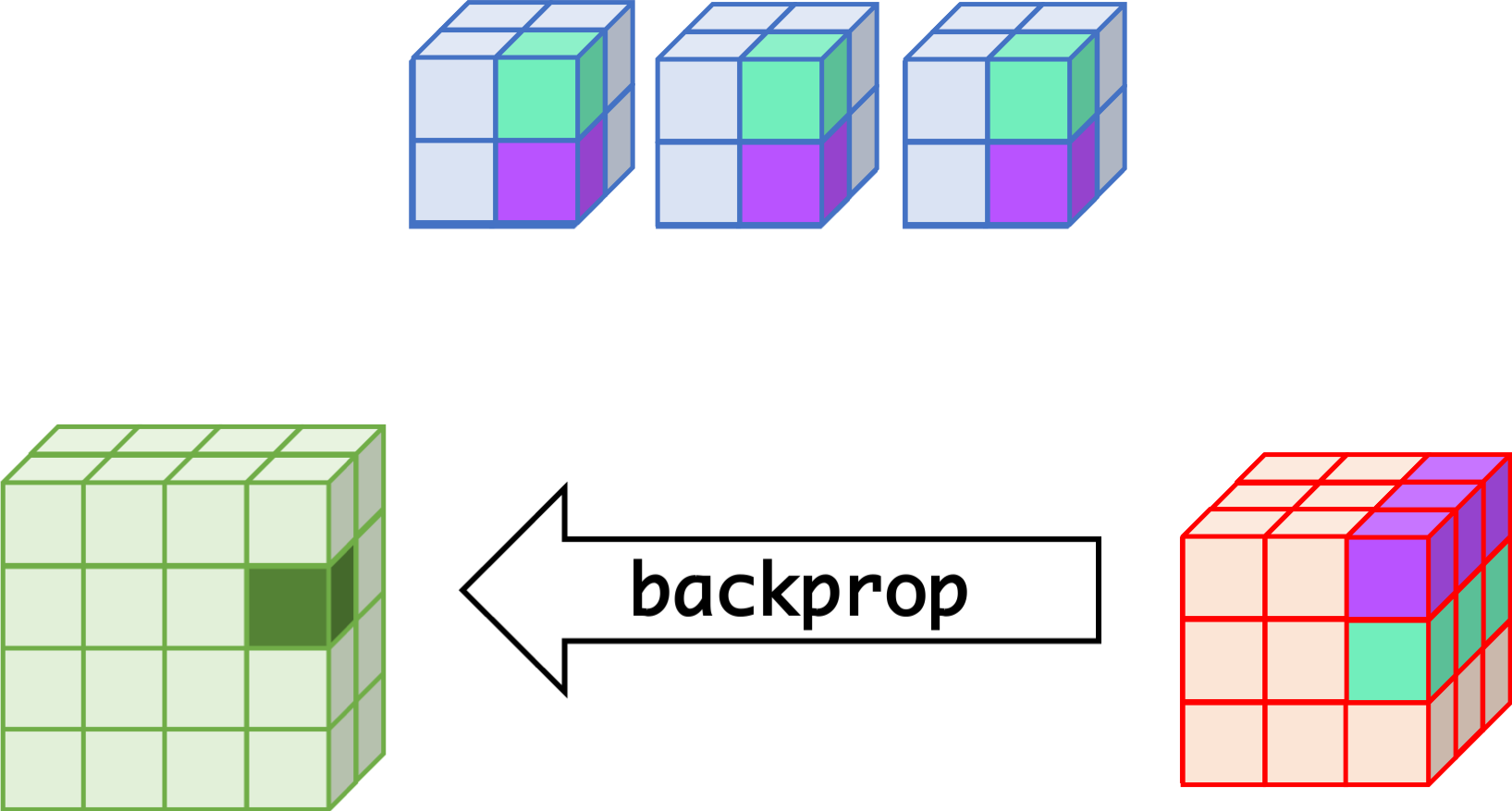 |
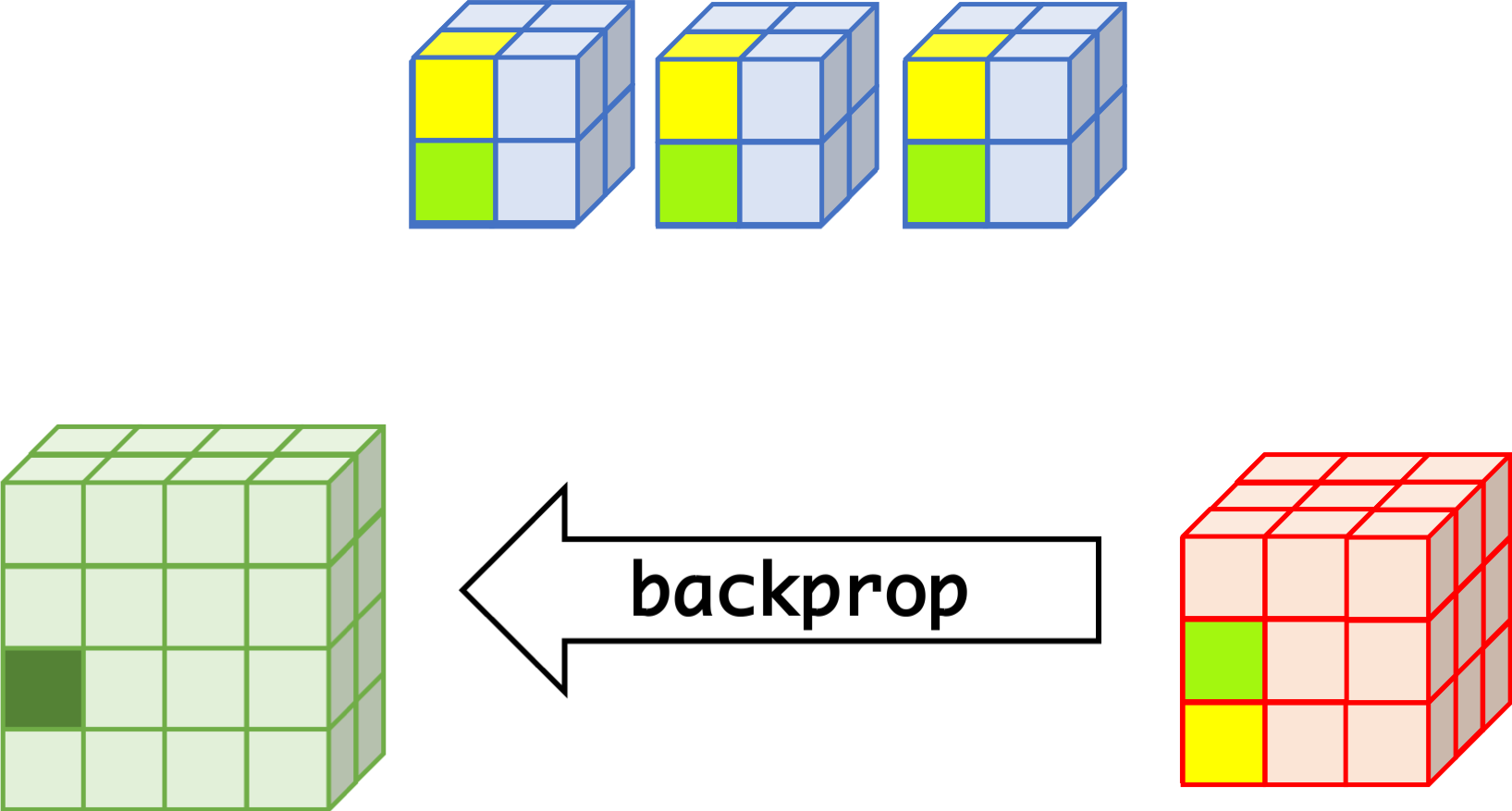 |
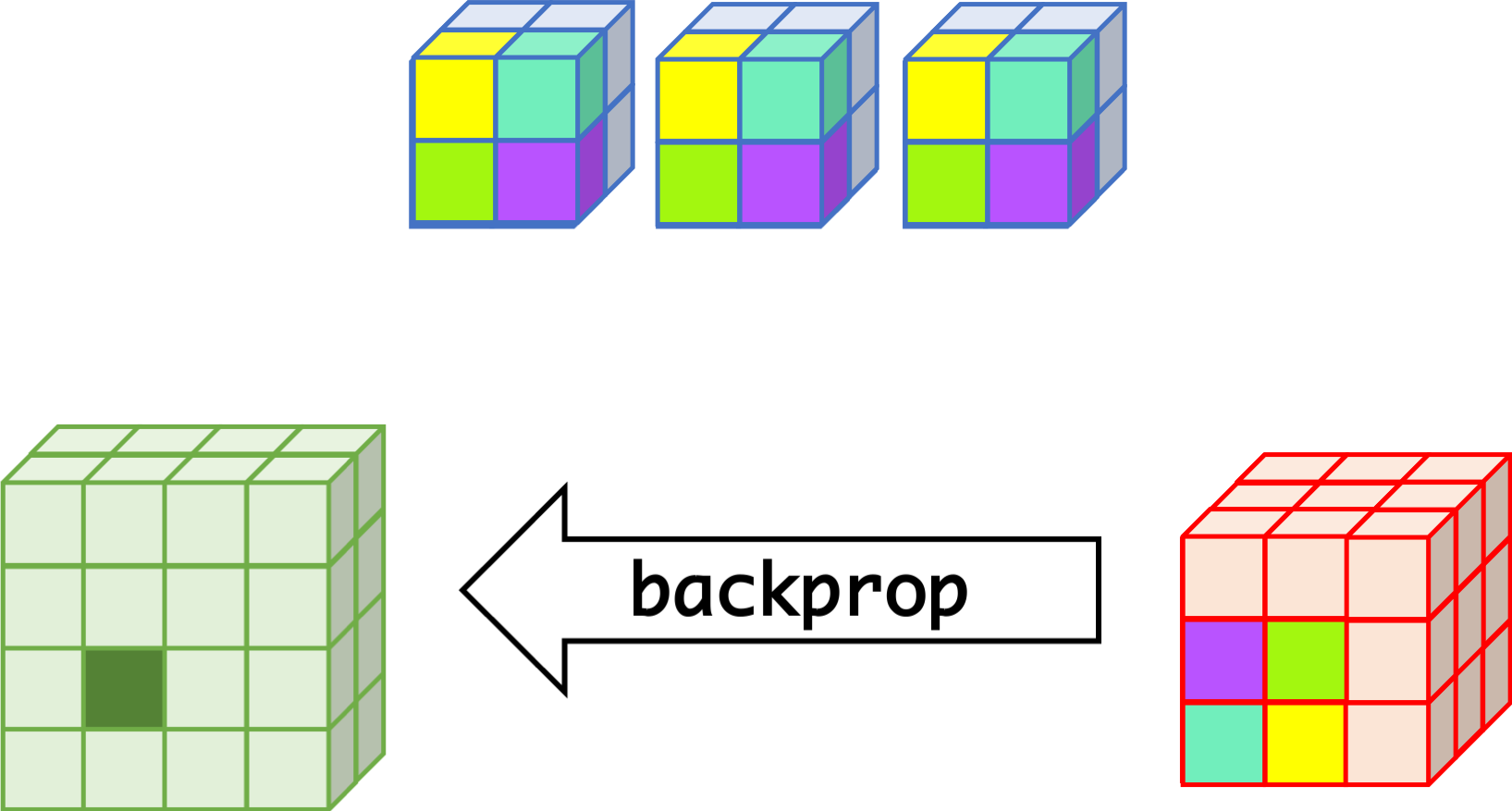 |
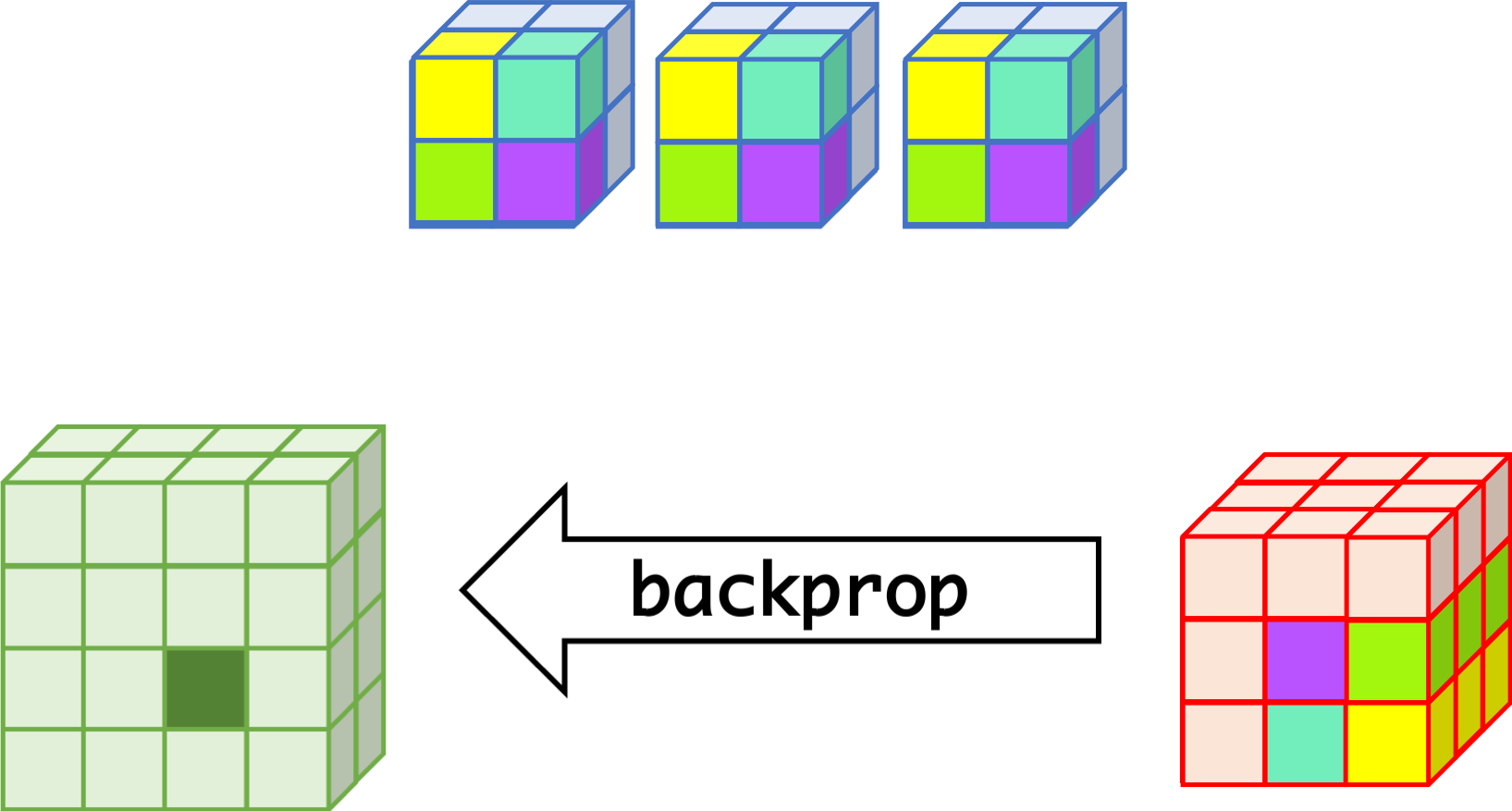 |
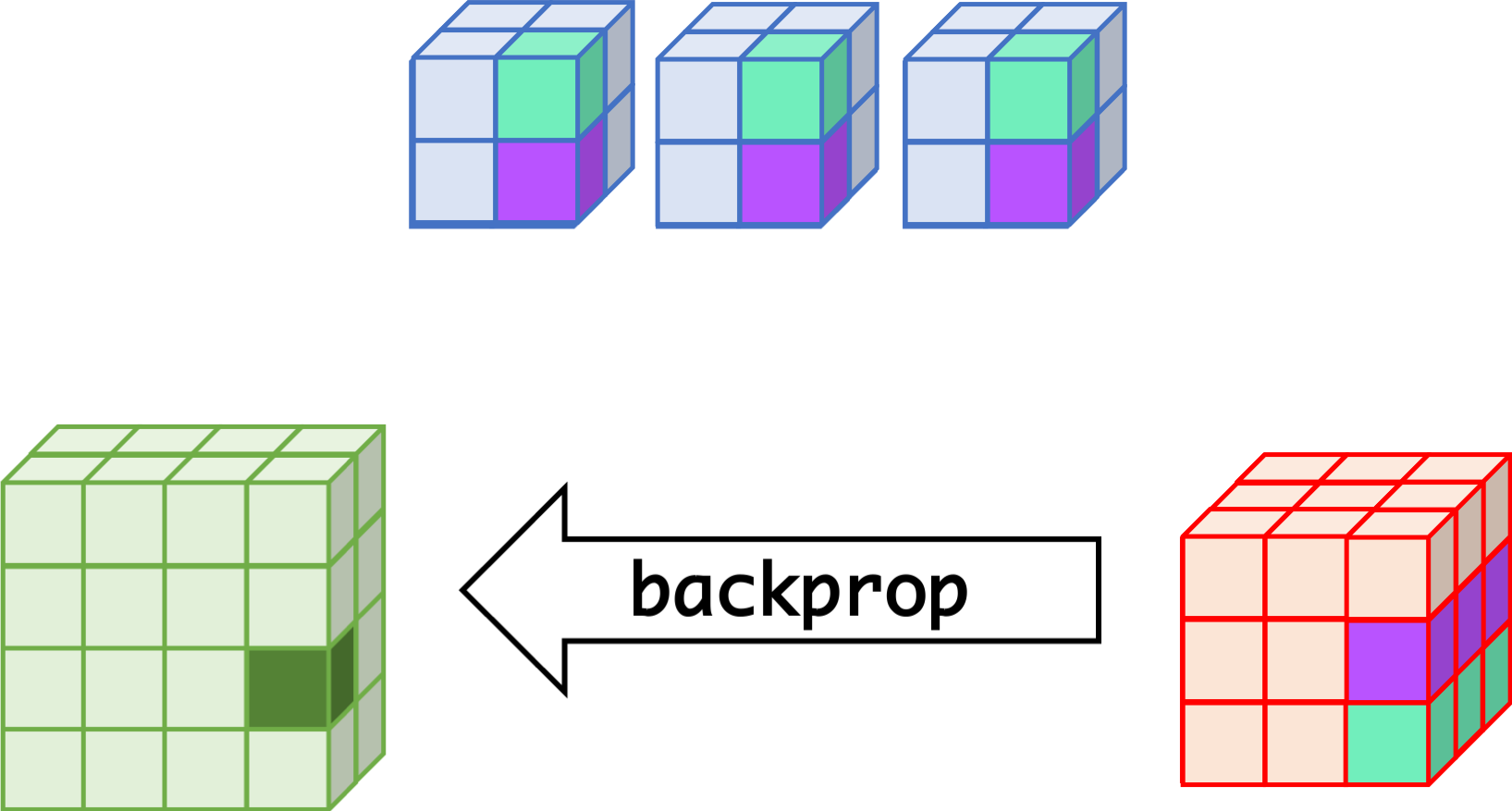 |
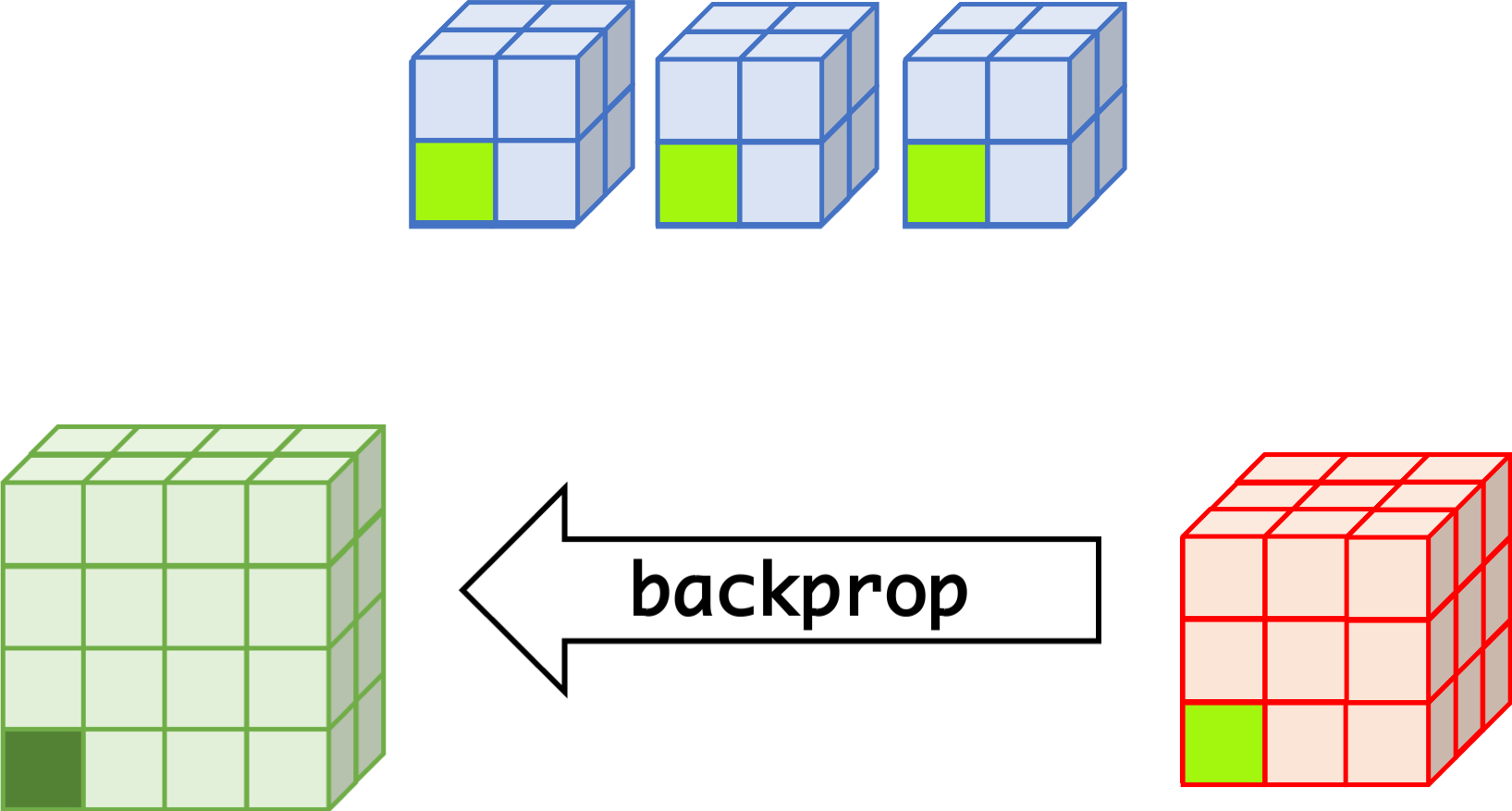 |
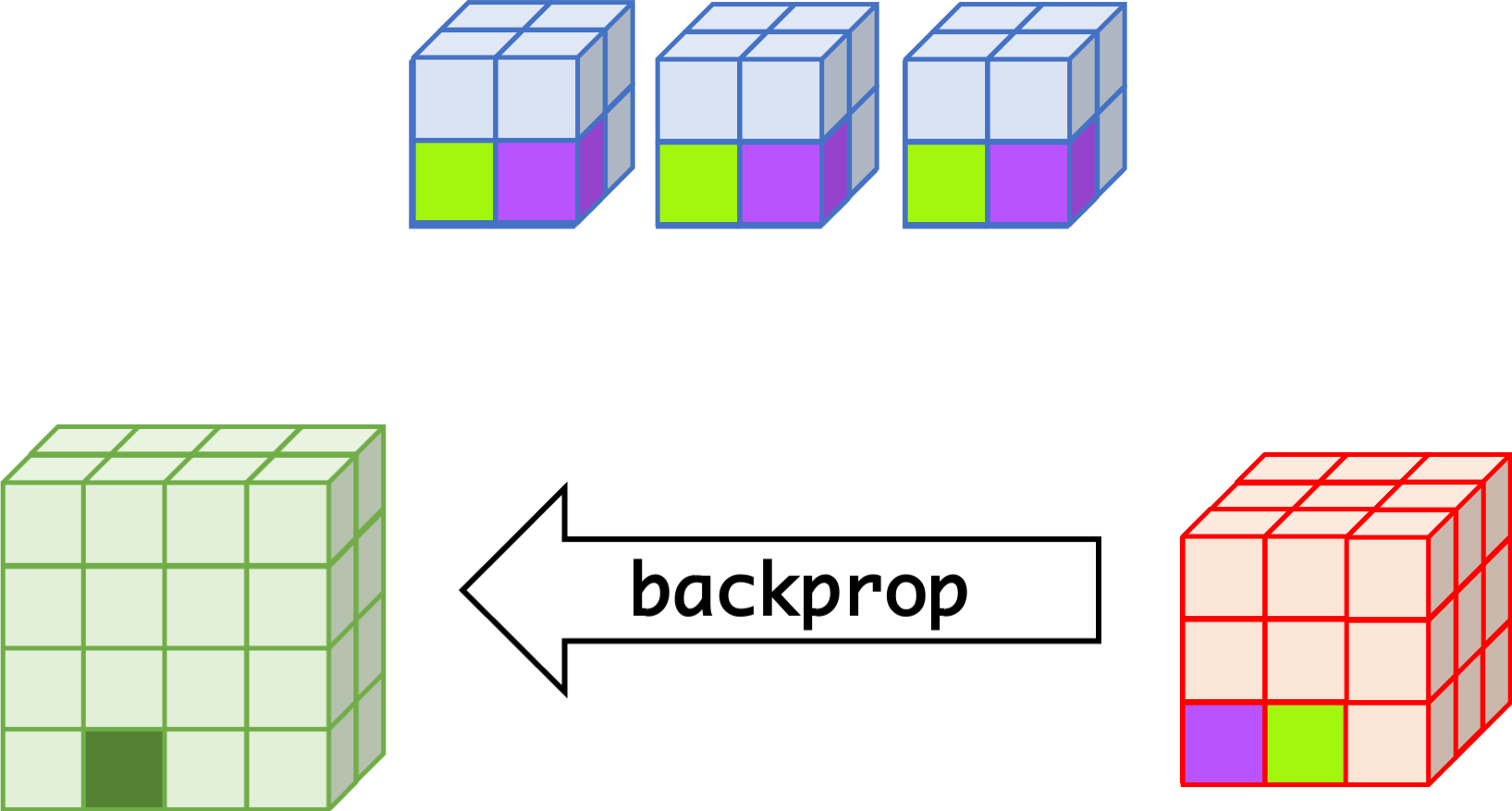 |
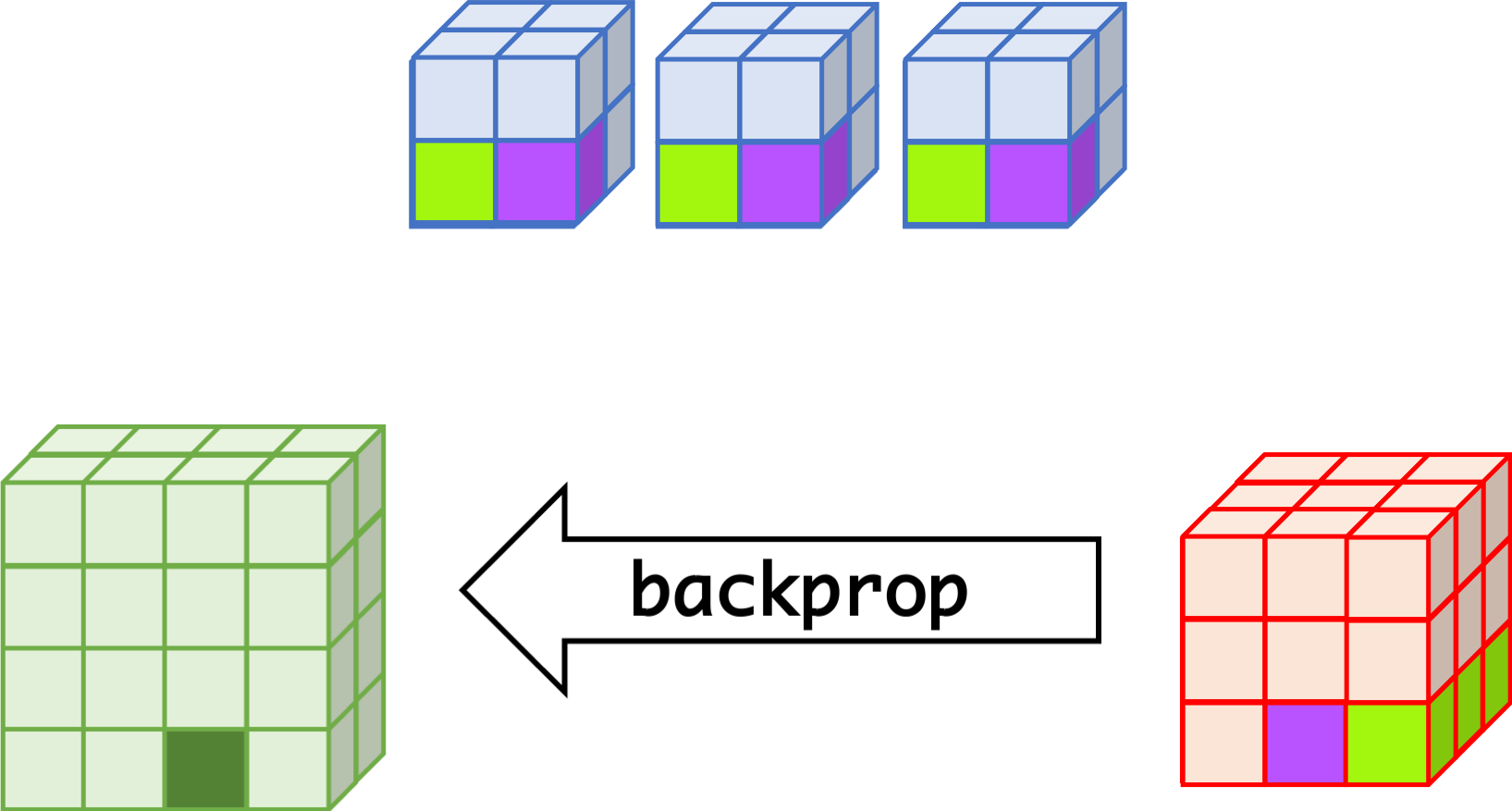 |
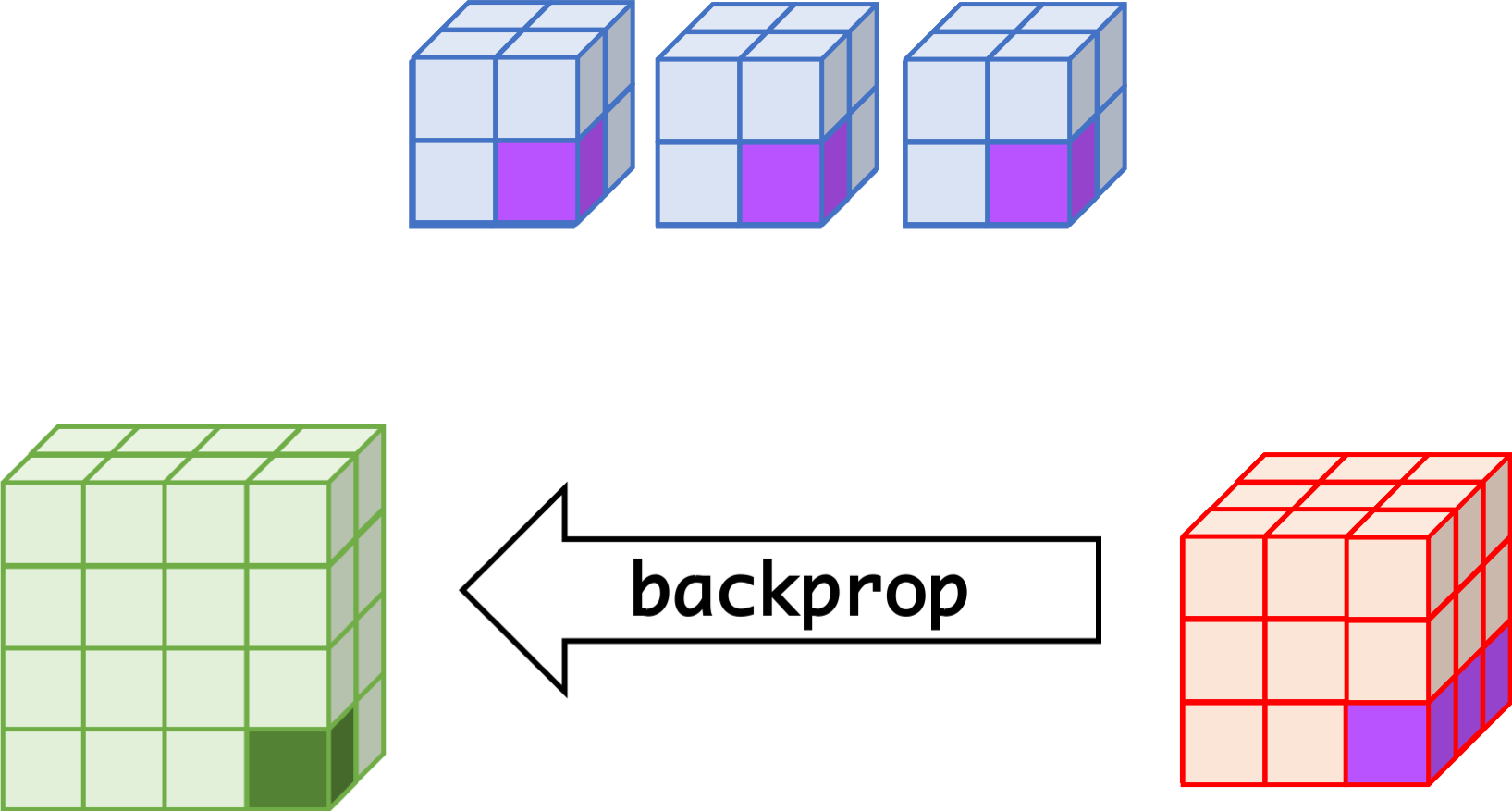 |
- $w_{m,n,c,c'}^k, b_{c'}^k$ $$ \begin{aligned} \frac{\partial E}{\partial w_{m,n,c,c'}^{k+1}} &= \sum_{i}\sum_{j}\frac{\partial E}{\partial a_{i,j,c'}^{k+1}}\frac{\partial a_{i,j,c'}^{k+1}}{\partial w_{m,n,c,c'}^{k+1}}\\ &= \sum_{i}\sum_{j}\frac{\partial E}{\partial a_{i,j,c'}^{k+1}}z_{i+m,j+n,c}^{k}\\ &= \sum_{i}\sum_{j}\delta_{i,j,c'}^{k+1}\cdot z_{i+m,j+n,c}^{k}\\ \frac{\partial E}{\partial b_{c'}^{k+1}} &= \sum_{i}\sum_{j}\delta_{i,j,c'}^{k+1} \end{aligned} $$
- $\delta_{i,j,c}^k$ $$ \begin{aligned} \delta_{i,j,c}^{k} &= \frac{\partial E}{\partial a_{i,j,c}^{k}} \\ &= \sum_{c'}\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}\left(\frac{\partial E}{\partial a_{i-m,j-n,c'}^{k+1}}\right)\left(\frac{\partial a_{i-m,j-n,c'}^{k+1}}{\partial a_{i,j,c}^k}\right)\\ &= \sum_{c'}\sum_{m=0}^{M-1}\sum_{n=0}^{N-1} \left(\delta_{i-m,j-n,c'}^{k+1}\right)\left(w_{m,n,c,c'}^{k+1}h'\left(a_{i,j,c}^k\right)\right) \\ &= h'\left(a_{i,j,c}^k\right)\sum_{c'}\sum_{m=0}^{M-1}\sum_{n=0}^{N-1} \delta_{i-m,j-n,c'}^{k+1}\cdot w_{m,n,c,c'}^{k+1} \end{aligned} $$
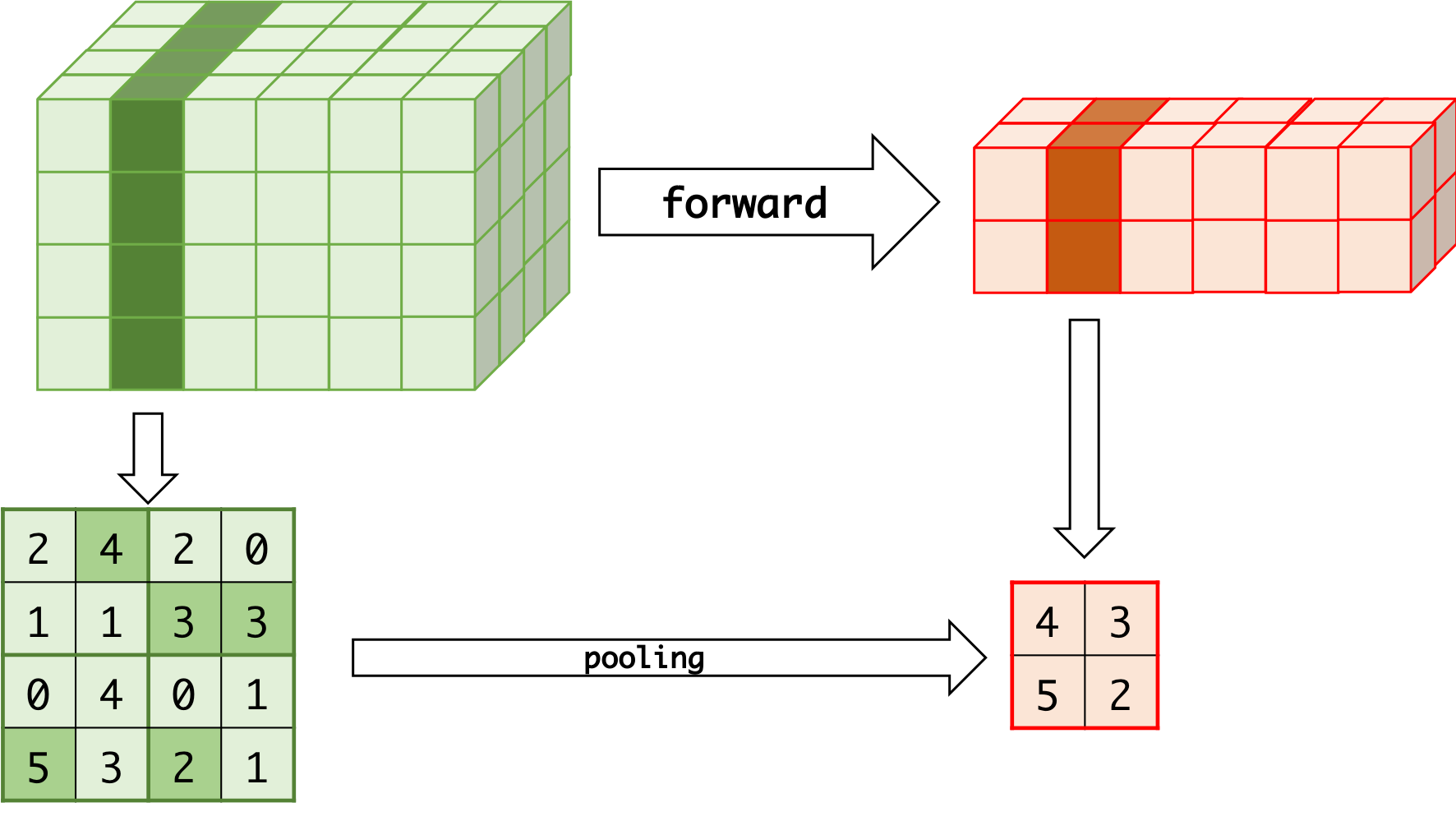
Pooling Layer
forward¶
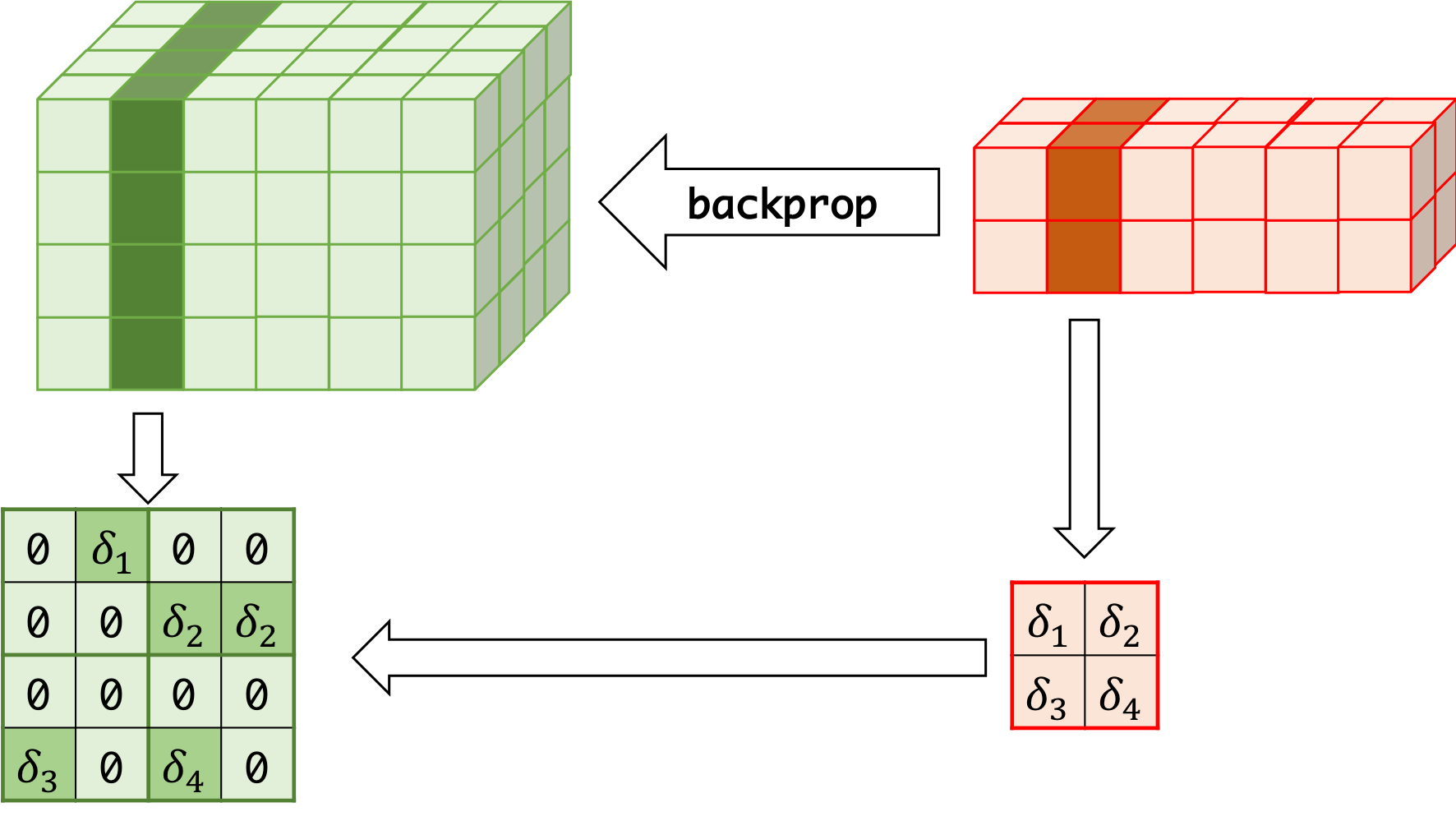
backprop¶
ex. MNIST¶
The MNIST database (Modified National Institute of Standards and Technology database) is a large (60,000 training images and 10,000 testing images) database of handwritten digits that is commonly used for training various image processing systems.
| 0 | 1 | 2 | 3 | 4 |
 |
 |
 |
 |
 |
| 5 | 6 | 7 | 8 | 9 |
 |
 |
 |
 |
 |
In [1]:
import numpy as np
from kerasy.datasets import mnist
from kerasy.models import Sequential
from kerasy.layers import Dense, Dropout, Flatten, Conv2D, MaxPooling2D, Input
from kerasy.utils import CategoricalEncoder
In [2]:
# Datasets Parameters.
num_classes = 10
n_samples = 1_000
# Training Parameters.
batch_size = 16
epochs = 20
keep_prob1 = 0.75
keep_prob2 = 0.5
In [3]:
# input image dimensions
img_rows, img_cols = 28, 28
In [4]:
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
In [5]:
x_train = np.expand_dims(x_train, axis=-1)
x_test = np.expand_dims(x_test, axis=-1)
input_shape = (img_rows, img_cols, 1)
In [6]:
x_train = x_train[:n_samples]
y_train = y_train[:n_samples]
x_test = x_test[:n_samples]
y_test = y_test[:n_samples]
In [7]:
x_train = x_train.astype('float64')
x_test = x_test.astype('float64')
x_train /= 255
x_test /= 255
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
In [8]:
# convert class vectors to binary class matrices
encoder = CategoricalEncoder()
y_train = encoder.to_onehot(y_train, num_classes)
y_test = encoder.to_onehot(y_test, num_classes)
In [9]:
model = Sequential()
model.add(Input(input_shape=input_shape))
model.add(Conv2D(32, kernel_size=(3, 3), activation='relu'))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(keep_prob=keep_prob1))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(keep_prob=keep_prob2))
model.add(Dense(num_classes, activation='softmax'))
In [10]:
model.compile(
optimizer='adagrad',
loss='categorical_crossentropy',
metrics=['categorical_accuracy']
)
In [11]:
model.summary()
In [12]:
model.fit(
x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test)
)
In [13]:
model.save_weights("MNIST_example_notebook_adagrad.pickle")