Tandem Repeats

2020-03-18(Wed)
Bio/tandem.py

Notebook

Example Notebook: Kerasy.examples.tandem.ipynb

Tandem Repeats

Tandem Repeats are simple sequence repeats that are extremely common throughout the genomes of a wide range of species. Tandem repeats are helpful to determine the inherited traits of gene from its parent and in determining the ancestor relationship. Tandem repeats are proven to be biologically significant as they can help in discovery of dynamic mutations for genetic diseases.

There are two main methods like dynamic programming, suffix array induced sorting, to find exact tandem repeats.

#	Suffix Array - Induced Sorting	Dynamic Programming
Construction	$$O\left(n\right)$$	$$O\left(n^2\right)$$
Tandem repeats discovery	$$O\left(n\ast m\right)$$	$$O\left(n^2\right)$$
Total time	$$O\left(n + n\ast m\right)$$	$$O\left(n^2\right)$$
Space complexity	$$O\left(n\right)$$	$$O\left(n^2\right)$$

here, $n$ is the length of the sequence and $m$ is the average length of the suffix.

The time required to identify tandem repeats mainly depends on construction of the required data structure.

For Dynamic programming method, a square matrix of size of the sequence is constructed and values are calculated which takes the time and space complexity of $O\left(n^2\right)$.
In SA-IS method, the time and space needed for construction is $O\left(n\right)$.

Dynamic Programming Method

class kerasy.Bio.tandem.find(method="DP")

To find all tandem repeats in a sequence we perform slight modifications to the Smith-Waterman algorithm for local alignments. The time complexity of the method will be $O\left(n\ast n\right)$ as we will be filling a two-dimensional matrix. We then align the sequence with itself to find tandem repeats.

The modifications we perform to the algorithm are:

Align the string with itself by placing the string on the top and on the left.
Set all diagonal elements to zero so we don't align a character by itself.
Since both strings are same, we only need to calculate one half of the matrix.
When calculating the next cell of the matrix, we
- assign a score of zero for mismatch or gap.
- just increment the score by one for match.
The scores in this matrix represent the length of the tandem repeat. We repeat the longest tandem repeat in the sequences. If we have multiple repeats of the same length, we repeat all of them.

Suffix Array - Induced Sorting Method

※ If you are not familiar with Suffix Array, please look at String Search page.

class kerasy.Bio.tandem.find(method="SAIS")

In Kerasy, we use the $O(n)$ searching method which is introduced in "Finding Maximal Repetitions in a Word in Linear Time"

Since various auxiliary data, theorems, and algorithms are used in this implementation, only the important ones are shown below.

s-factorization

s-factorization, or Lempel-Ziv(LZ77) decomposition of a string $S$ is a factorization $S=f_1\cdots f_n$ where each factor $f_k$ is either

a single character if that character does not occur in $f_1\cdots f_{k-1}$.
the longest prefix of the rest of the string which occurs at least twice in $f_1\cdots f_{ks}$.

Most recent efficient linear time algorithms are off-line, running in $O\left(N\right)$ time for integer alphabets using $O\left(N\right)$ space. They first construct the suffix array of the string, then compute two arrays called Longest Common Prefix(LCP) array, and Longest Previous Factor(LPF) array from which the LZ factorization can be easily computed.

Theorem 5 (paper1)

Let $w=u_1u_2\cdots u_k$ be the s-factorization of $w$, and let $r$ be a maximal repetition in $w$, we can classify $r$ into two classes:

$$ \begin{aligned} &\begin{cases} \text{initpos}(r)\leq\text{initpos}(u_i)\\ \text{initpos}(u_i)\leq\text{endpos}(r) < \text{endpos}(u_i) \end{cases}&\cdots\left(\text{type}1\right)\\ &\text{initpos}(u_i) < \text{initpos}(r) < \text{endpos}(r) < \text{endpos}(u_i)&\cdots\left(\text{type}2\right)\\ \end{aligned} $$

See more detail: Simpler and Faster Lempel Ziv Factorization

Find repetitions of (type1)

rightmax periodicities

Let us focus on maximal repetitions $r$ which have a period in $u$. (rightmax periodicities) We need two auxiliary functions:

Name	Domain	Definition	Description
$$LP(i)$$	$$2\leq i \leq n+1$$	$$LP(i) = \begin{cases}\max\left\{j\mid u[1\ldots j] = u[i\ldots i+j-1]\right\}&\left(2\leq i\leq n\right)\\0 &\left(i=n+1\right)\end{cases}$$	$LP(i)$ is the length of the longest prefix of $u$ which is also a prefix of $u[i\ldots n]$
$$LS(i)$$	$$1\leq i \leq n$$	$$LS(i) = \max\left\{j\mid t[m-j+1\ldots m] = v[m+i-j+1\ldots m+i]\right\}$$	$LS(i)$ is the length of the longest suffix of $t$ which is also a suffix of $tu[1\ldots i]$.

Theorem 5.1 (paper2)

Let

$m = |t|, n = |u|$
$j$ is an integer.
$r$ is a substring of $tu$ with at least one character in $t$ and at least $j$ characters in $u$, and with $|r|\geq2j$.

Then, $r$ is a periodicity with period length $j$ iff it begins at or after $t[m-LS(j)+1]$ and ends at or before $u[j+LP(j+1)]$.

Proof 5.1 (paper2)

Let

$a > 0$ be the number of characters of $r$ in $t$
$b \geq 0$ be the number of characters of $r$ in $u[j+1\ldots n]$
$i=|r|= a+b+j$

For $r$ to be a periodicity with period length $j$, it is necessary and sufficient for the first $i-j$ characters of $r$ to match the last $i-j$ characters of $r$. ($r[1\ldots a+b]$ matches $r[1+j\ldots i]$.)

This can be broken into two separate conditions:

$r[1\ldots a]$ matches $r[1+j\ldots a+j]$
$r[a+1\ldots a+b]$ matches $r[a+j+1\ldots i]$

These condition is equivalent to

requiring "$r[1+j\ldots a+j]=r[1+j]\ldots u[j]$ is suffix of $t$" is equivalent to requiring "$r$ to begin at or after $t[m-LS(j)+1]$."
$$\begin{aligned} &(a+j)-(1+j)+1\leq LS(j)\\ \Longleftrightarrow &a\leq LS(j) \\ \Longleftrightarrow &m-\text{initpos}(r)+1\leq LS(j)\\ \Longleftrightarrow &\text{initpos}(r)\geq m-LS(j)+1 \end{aligned}$$
requiring $r[a+j+1\ldots i]=u[j+1]\ldots r[i]$ is prefix of $u$, so this is equivalent to requiring $r$ to end at or before $u[j+LP(j+1)]$
$$\begin{aligned} &i-(a+j+1)+1\leq LP(j+1)\\ \Longleftrightarrow &b\leq LP(j+1)\\ \Longleftrightarrow &\text{endpos}(r)-(m+j)\leq LP(j+1)\\ \Longleftrightarrow &\text{endpos}(r)\leq m+j+LP(j+1) \end{aligned}$$

Thus, conditions $1$ and $2$ together are equivalent to the requirement stated in Theorem 5.1.

Theorem 5.2 (paper2)

Let $j(1\leq j\leq n)$ is an integer. There exists a rightmax periodicity (in $tu$) with period length $j$ iff $LS(j)+LP(j+1)\geq j$. When this inequality holds, there is exactly one rightmax periodicity with period length $j$, and this periodicity occurs at $t[m-LS(j)+1]\ldots u[j+LP(j+1)]$

Proof 5.2 (paper2)

If the inequality fails, then there can be no substring of length $2j$ or more which meets the beginning and ending requirements of Theoreme 5.1, and hence no periodicity with period length $j$ occurs with at least one character in $t$ and at least $j$ characters in $u$. This implies there are no rightmax periodicities (in $tu$) with period length $j$.

On the other hand, if the inequality holds, then Theoreme 5.1 states that every substring (with length $2j$ or more) which starts in $t[m-LS(j)+1\ldots m]$ and ends in $u[j\ldots j+LP(j+1)]$ is a periodicity with period length $j$.

Moreover, these are the only such periodicities which have at least one character in $t$ and at least one period length in $u$. Of these periodicities, only one is maximal - the one that starts as far left as possible ($t[m-LS(j)+1]$) and continues as far right as possible ($u[j+LP(j+1)]$).

leftmax periodicities

As described in the table below, we can find leftmax periodicities (type1) symmetrically.

rightmax periodicities	leftmax periodicities

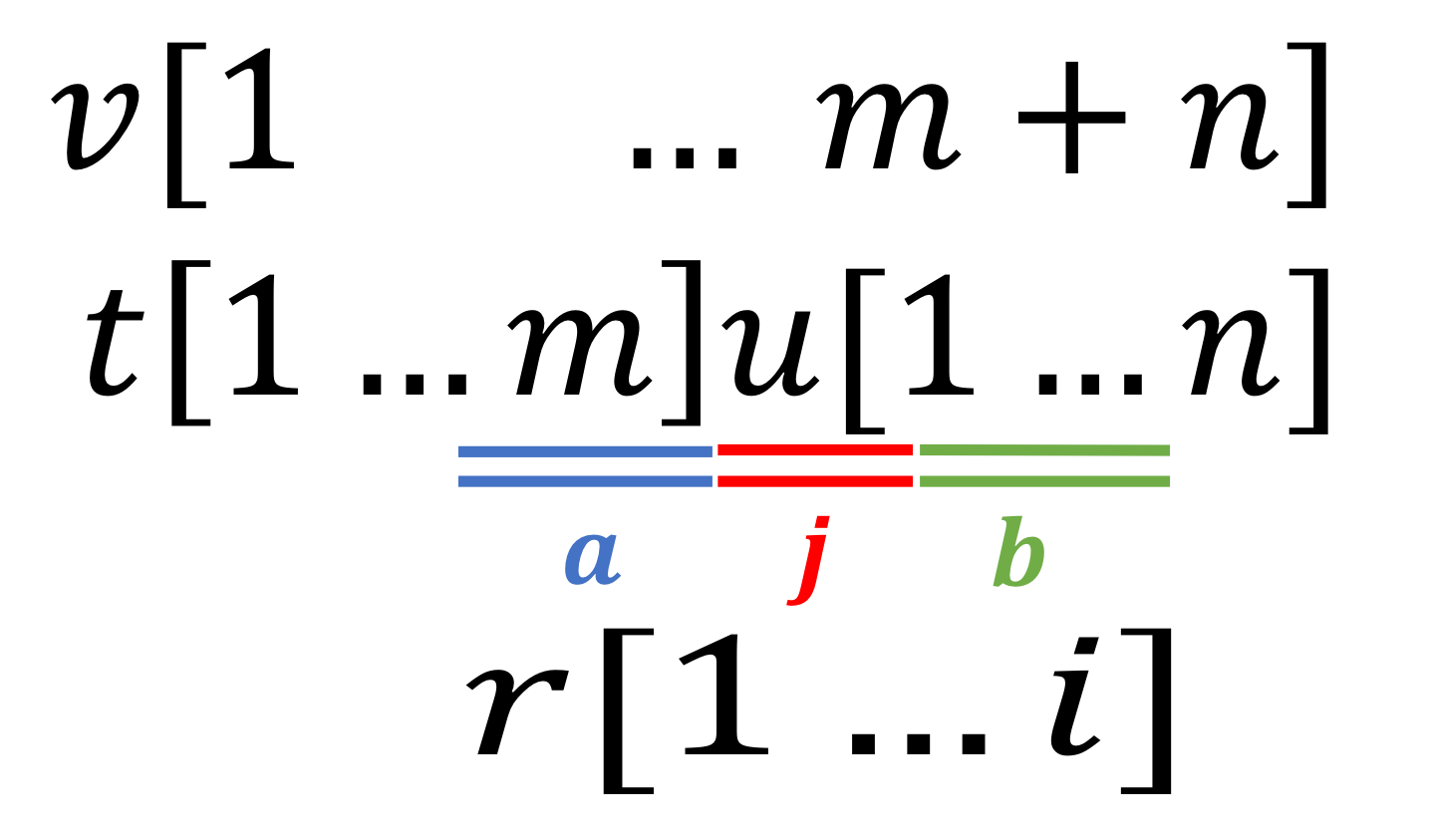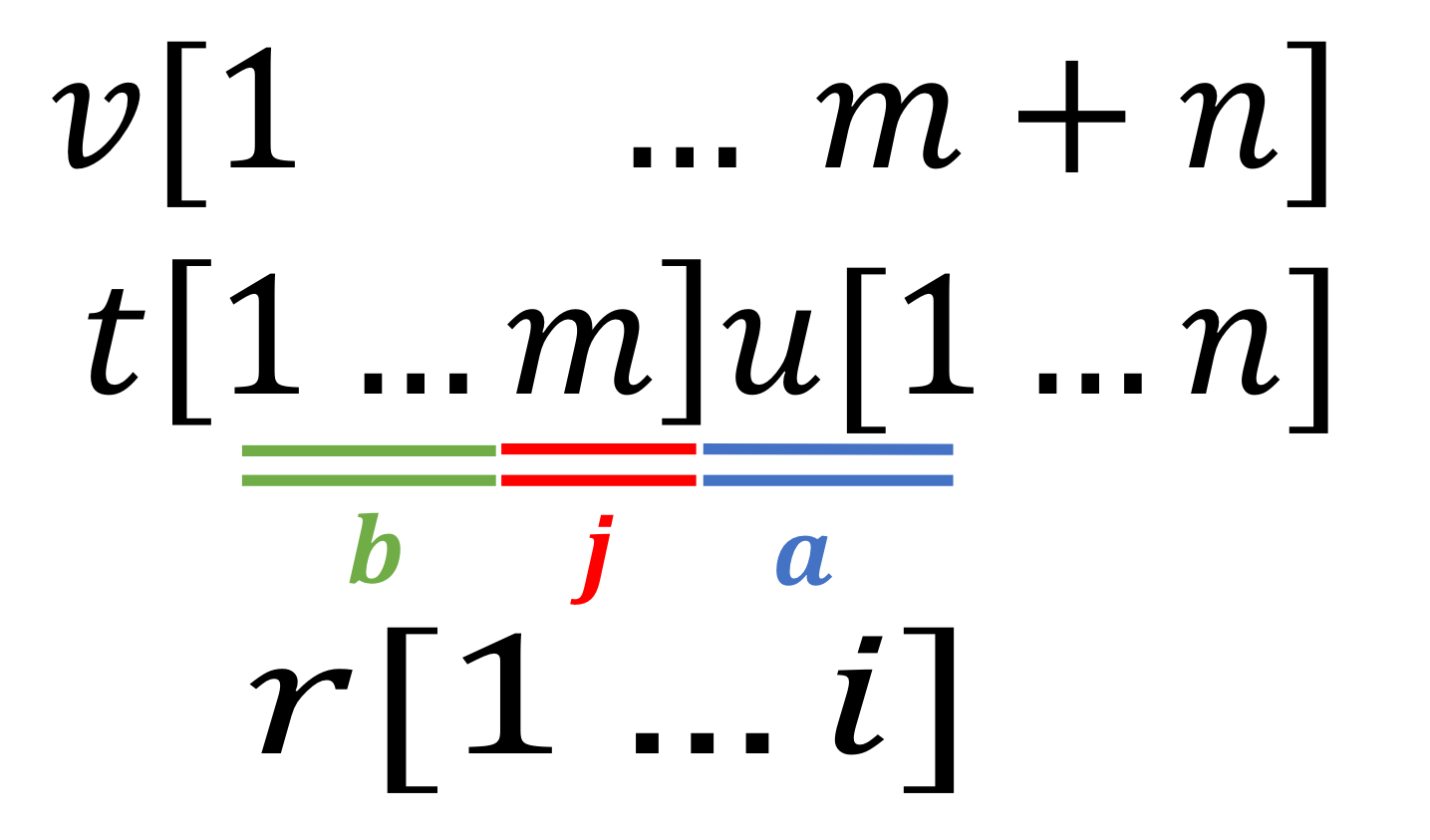maximal repetitions $r$ which have a *period* in $u$	maximal repetitions $r$ which have a *period* in $t$

Find repetitions of (type2)

The task is greatly simplified by the fact that every repetition of type 2 occurs entirely inside some s-factor $u_i$ and each $u_i$ has an earlier occurrence in $w$.

Let $v_i$ be thhe earlier occurrence of $u_i$, and let $\Delta_i = \text{initpos}(u_i) - \text{initpos}(v_i).$ Obiously, each repetition of type2 occurring inside $u_i$ is a copy of a maximal repetition occurring inside $v_i$ shifted by $\Deltai$ to the right.

Reference

terminology

Name	symbol	Description
word	$$w$$	$$w = a_1a_2\ldots a_n$$
subword	$$w[i\ldots j]$$	$$w[i\ldots j] = a_i\ldots a_j$$
position	$$\pi$$	Each position $\pi$ in $w$ defines a factorization $w = w_1w_2$ where $\mid w_1\mid=\pi$. A position in a word $w = a_1a_2\ldots a_n$ is an integer between $0$ and $n$, and the position of letter $a_i$ in $w$ is $i-1$.
initpos, endpos	$$initpos(v), endpos(v)$$	If $v=w[i\ldots j]$, we denote $initpos(v) = i-1$ and $endpos(v)=j$.
cross		We say that subword $v=w[i\ldots j]$ crosses a position $\pi$ in $w$, if $i\leq\pi<j$
root	$u$	If $w$ is a subword of $u^n$ for some natural $n$, $\mid u \mid$ is called a *period* of $w$, and word $u$ is a *root* of $w$.
*period*	$$p$$	smallest positive integer such that $a_i=a_{i+p}$ for all $i$, provided $1\leq i, i+p\leq n$.
minimal period	$$p(w)$$	Each word $w$ has the minimal period $p(w)$ and call *the* period of $w$.
exponent	$$e(w)$$	The ratio $\frac{\mid w\mid}{p(w)}$ is called the exponent of $w$ and denoted $e(w)$.
primitive		a root $u$ of $w$ such that $\mid u\mid = p(w)$, is *primitive*, that is $u$ cannot be written as $v^k$ for $k\geq2$.
repetition	$$r$$	A *repetition* in $w$ is any subword occurrence $r=w[i\ldots j]$ with $e(r)\geq2$
maximal repetition		A *maximal repetition* in $w$ is a repetition $r=w[i\ldots j]$ such that $p\left(w[i\ldots j]\right) < p\left(w[i-1\ldots j]\right)$ whenever $i > 1$, and $p\left(w[i\ldots j]\right) < p\left(w[i\ldots j+1]\right)$ whenever $j < n$.