String Search
Notebook
Example Notebook: Kerasy.examples.string.ipynb
Suffix Array
def kerasy.Bio.string.SAIS(string)
Suffix array is a sorted array of all suffixes of a string, and can be built in \(\mathrm{O}(n)\). This procedure is as following:
- Define the each character S/L-type.
- Find the LMS(Left Most S-type)
- Fill in \(-1\) to initialize Suffix Array.
- Prepare the empty buckets whose sizes are correspond to the Initial character grouping.
- Sort the LMS
- Scan SA in forward order and fill L-type suffixes.
- Scan SA in backward order and fill S-type suffixes.
Step1. Definition of S/L-type
- If \(i\)-th suffix is [smaller, bigger] then \(i+1\)-th suffix in lexicographical order, \(i\)-th character is [S,L]-type. Exceptionally, "$" is the initial character and defined S-type.
- In the above definition, obviously the following holds:
- \(i\)-th suffix is S-tyep when
- \(S[i]\) = "$"
- \(S[i] < S[i+1]\)
- \(S[i] == S[i+1]\) and \(i+1\)-th suffix is S-type.
- \(i\)-th suffix is L-tyep when
- \(S[i] > S[i+1]\)
- \(S[i] == S[i+1]\) and \(i+1\)-th suffix is L-type.
- \(i\)-th suffix is S-tyep when
| \(i=5\) | \(i=4\) | \(i=3\) |
|---|---|---|
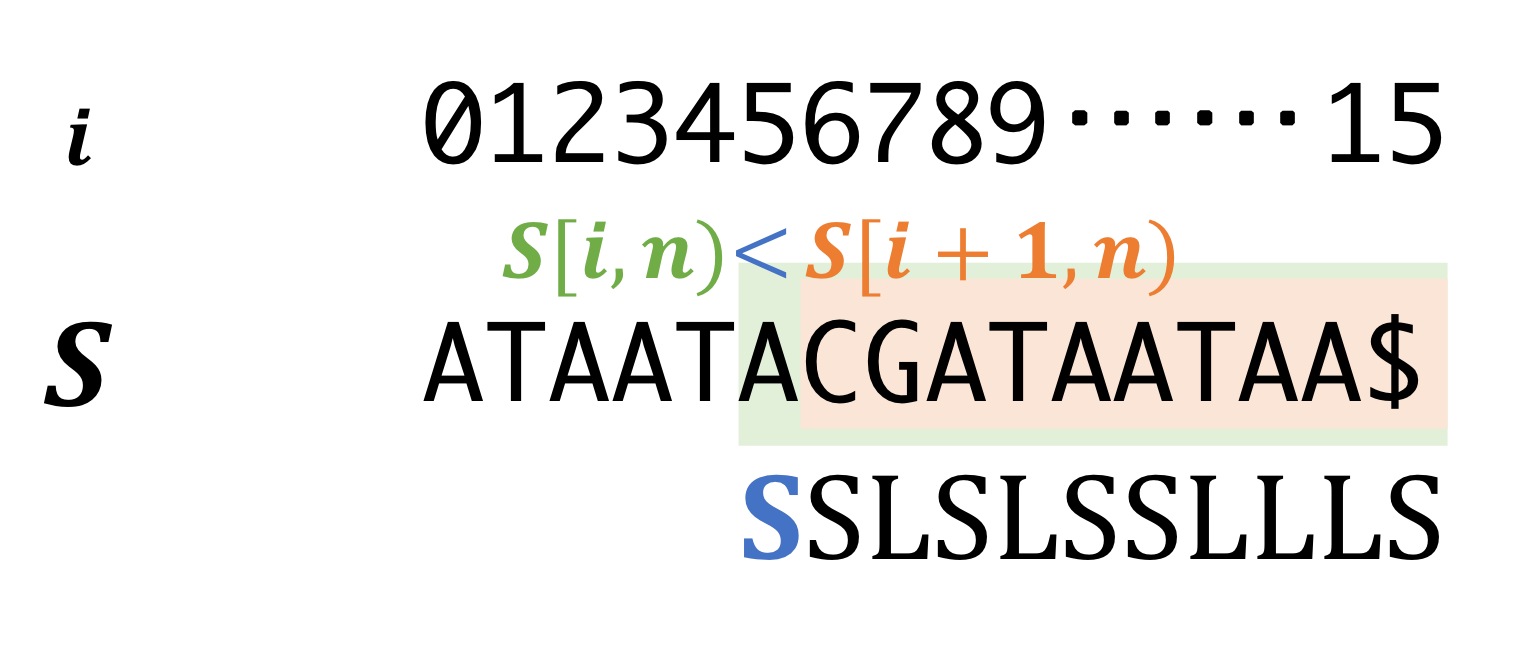 |
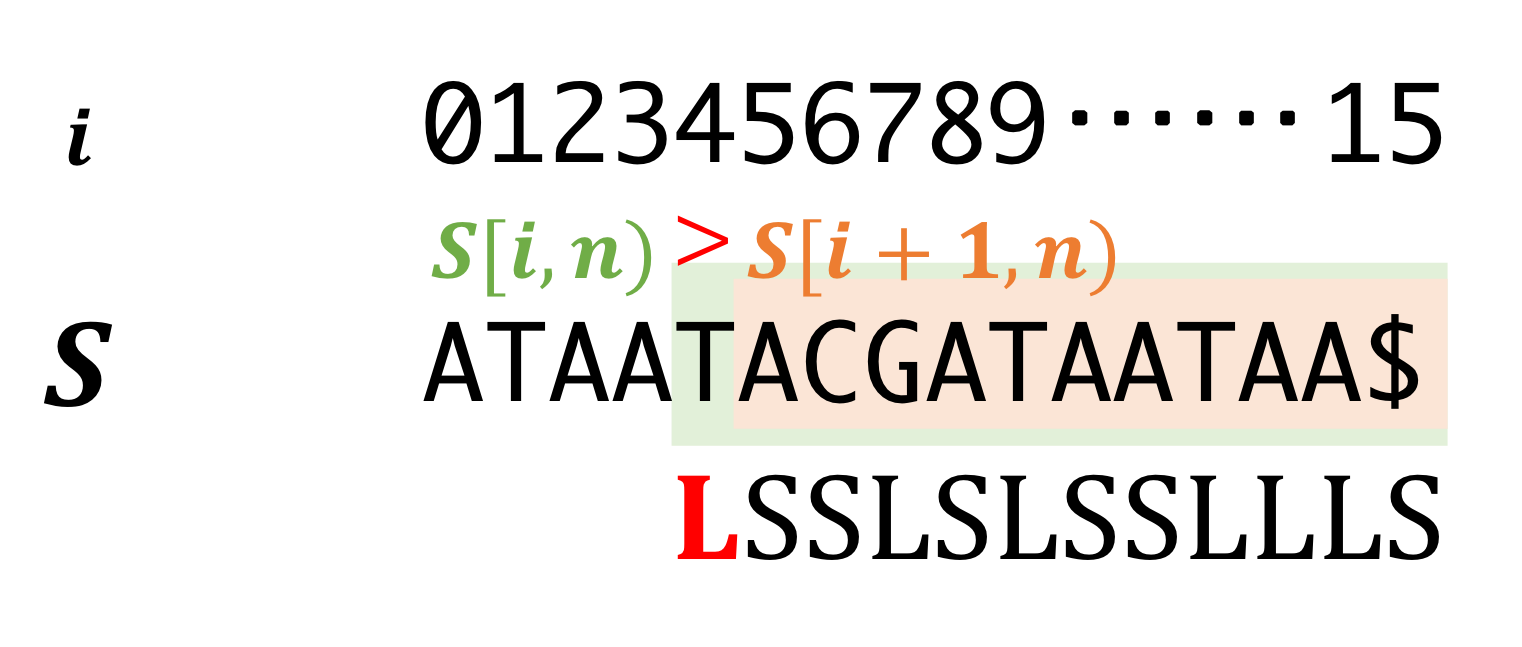 |
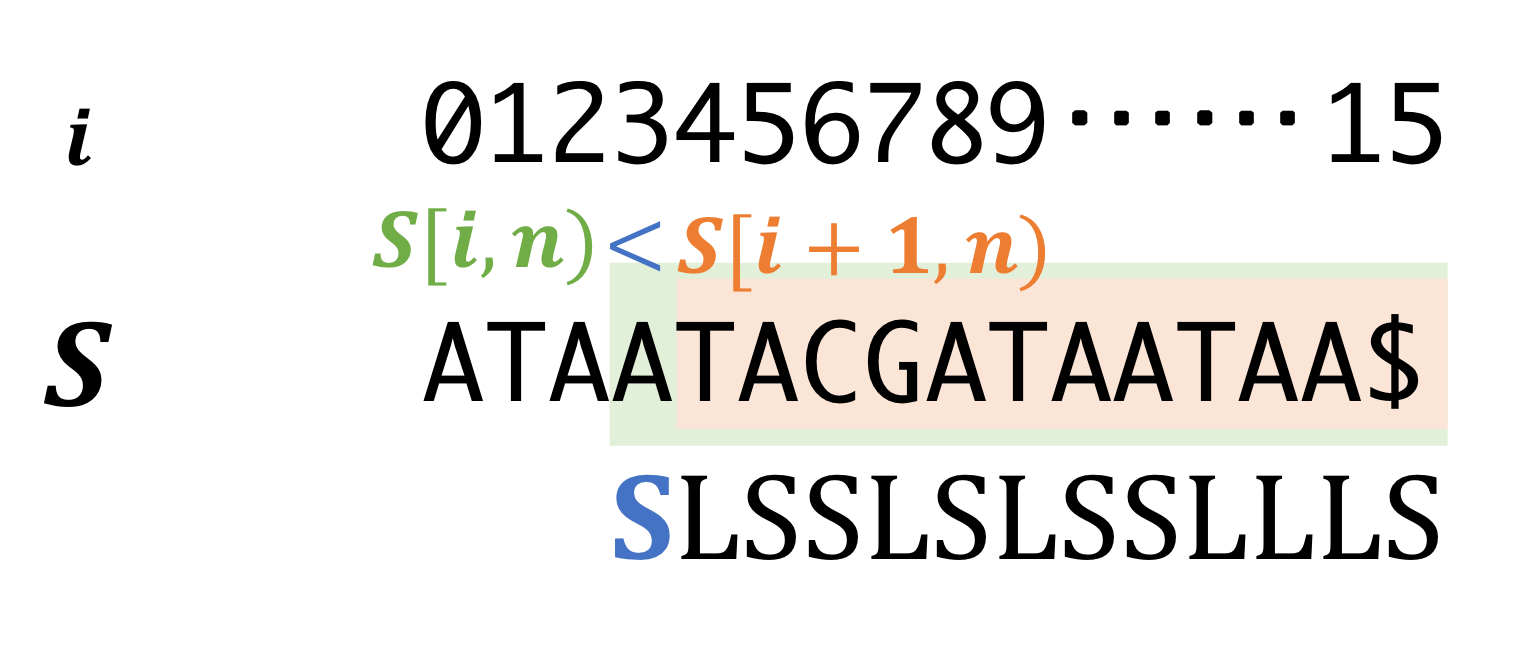 |
Step2. Definition of LMS
If \(S[i]\) is the S-type character and \(S[i-1]\) is the L-type, \(S[i]\) is called LMS(Left Most S-type).

Step3. Initialize Suffix Array.
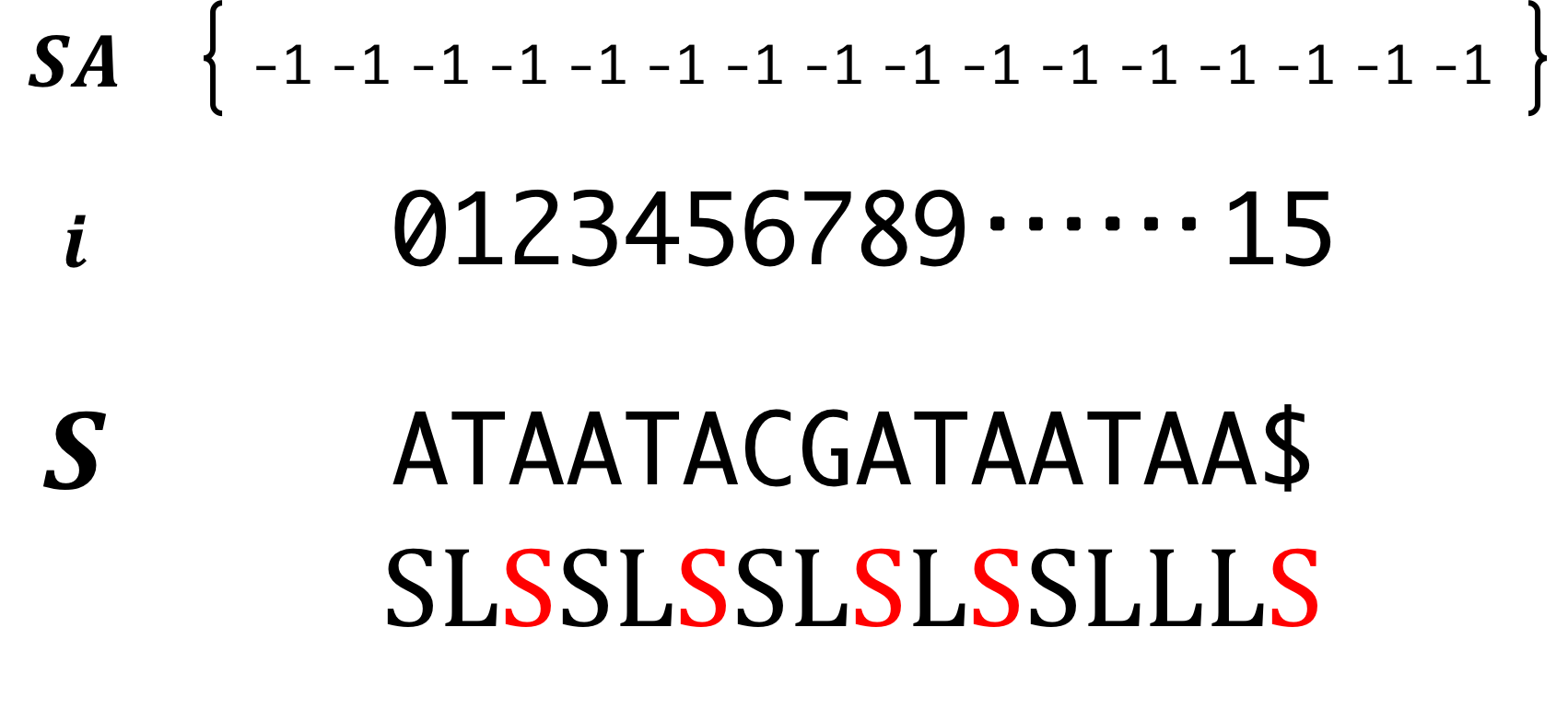
Step4. Prepare the empty buckets

Step5. Sort the LMS
※ This sorting is not easy, but ignore for consistency of explanation. (Touch again later.)
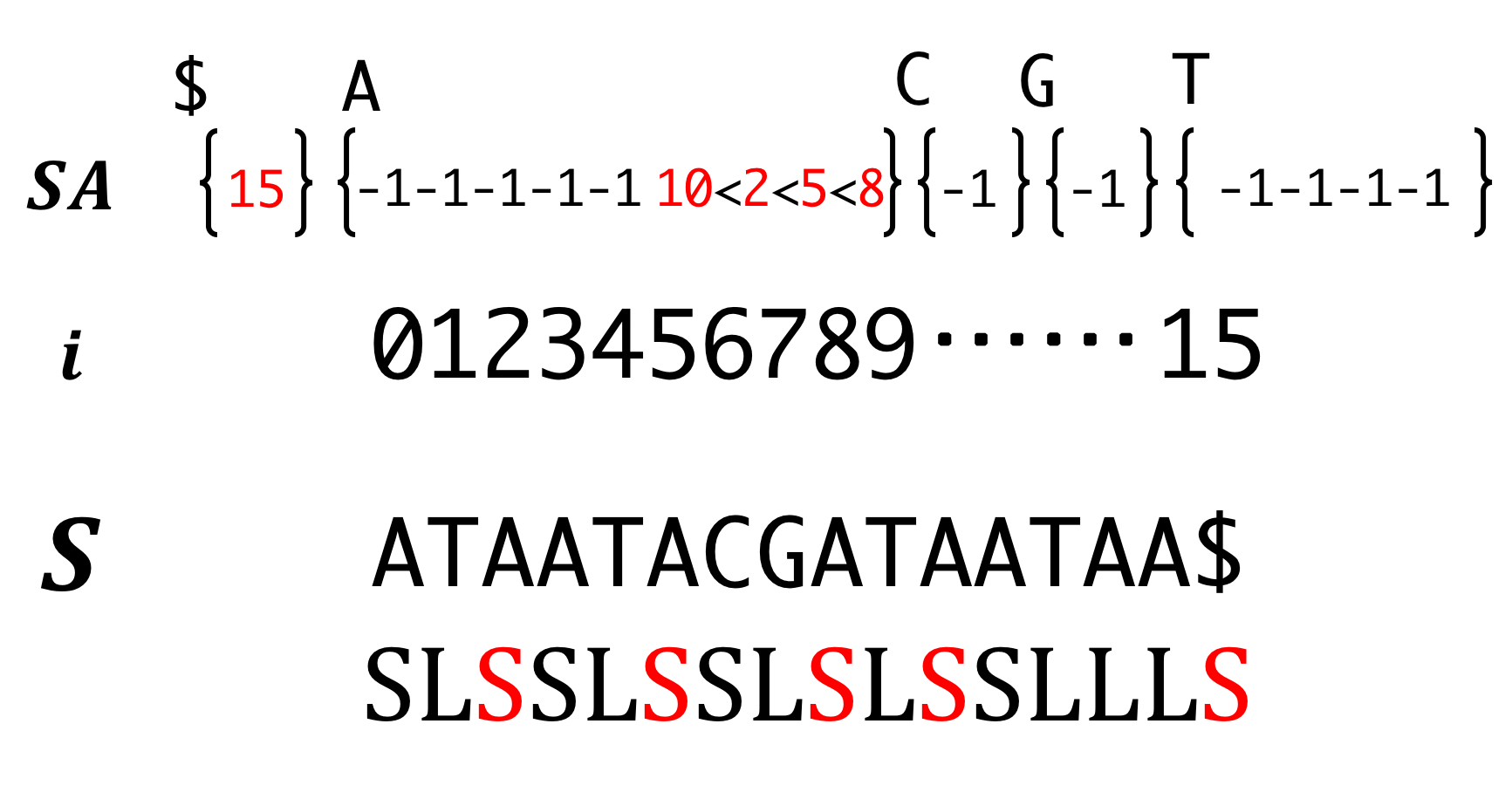
Induced Sorting
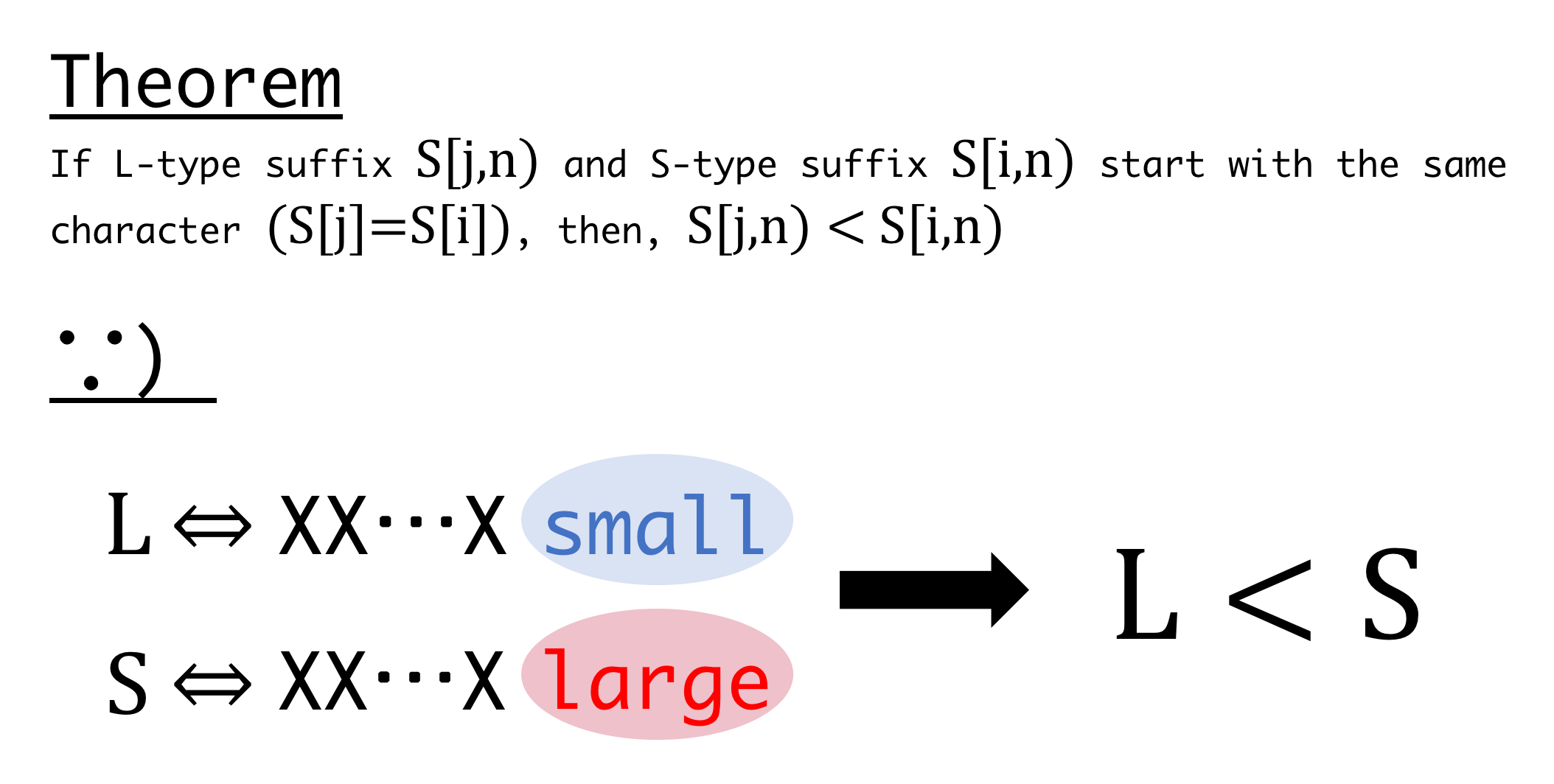
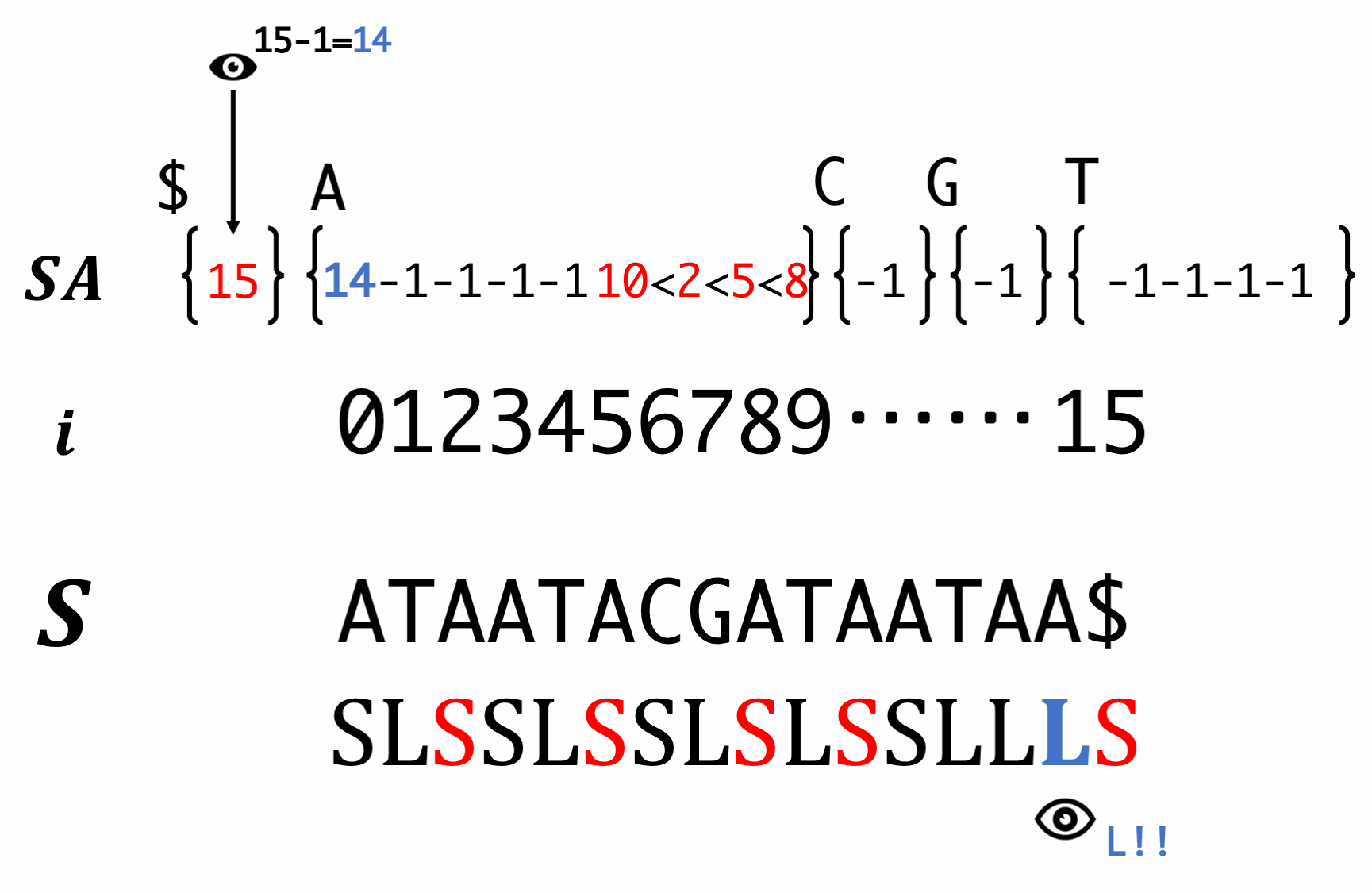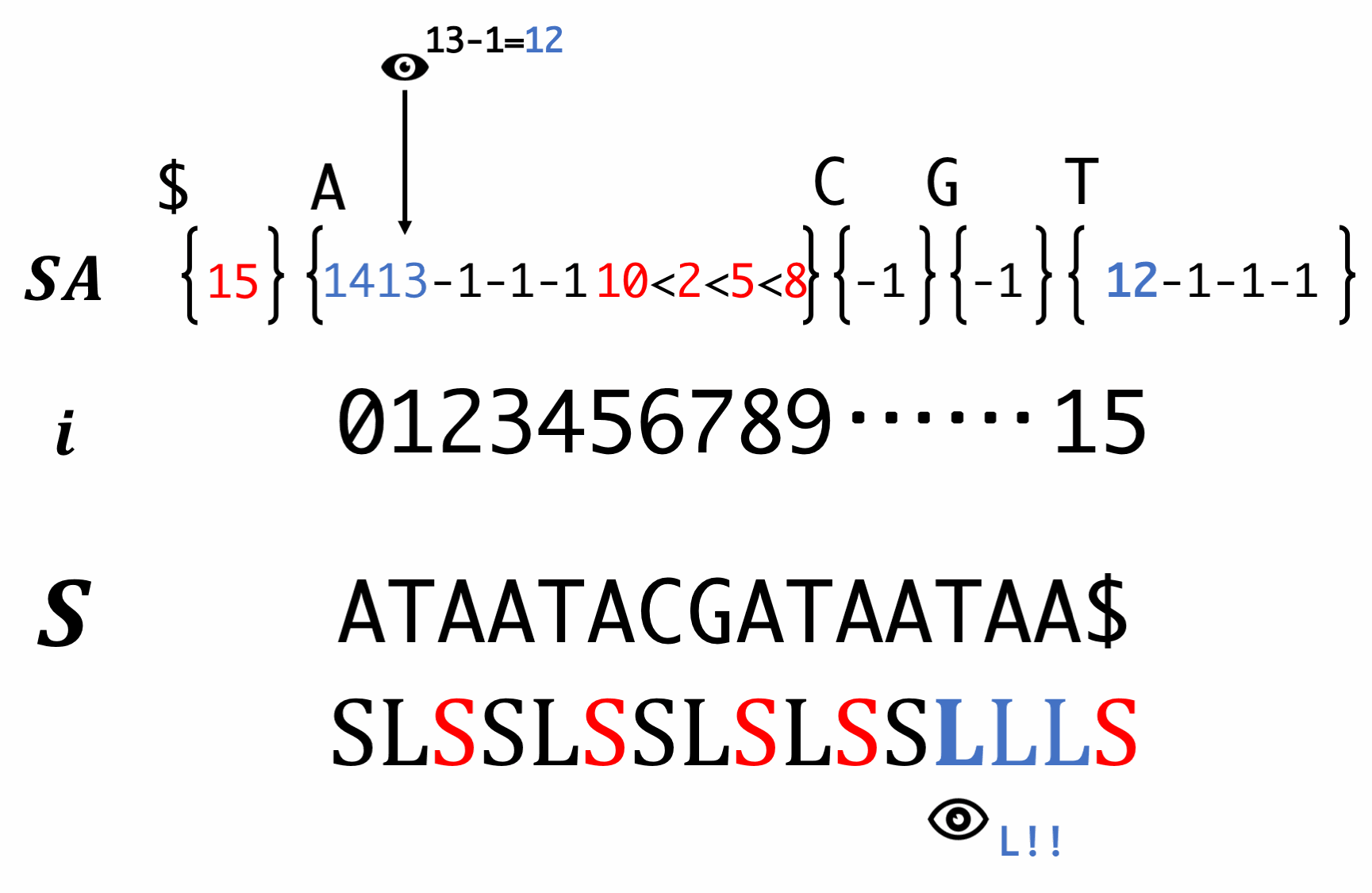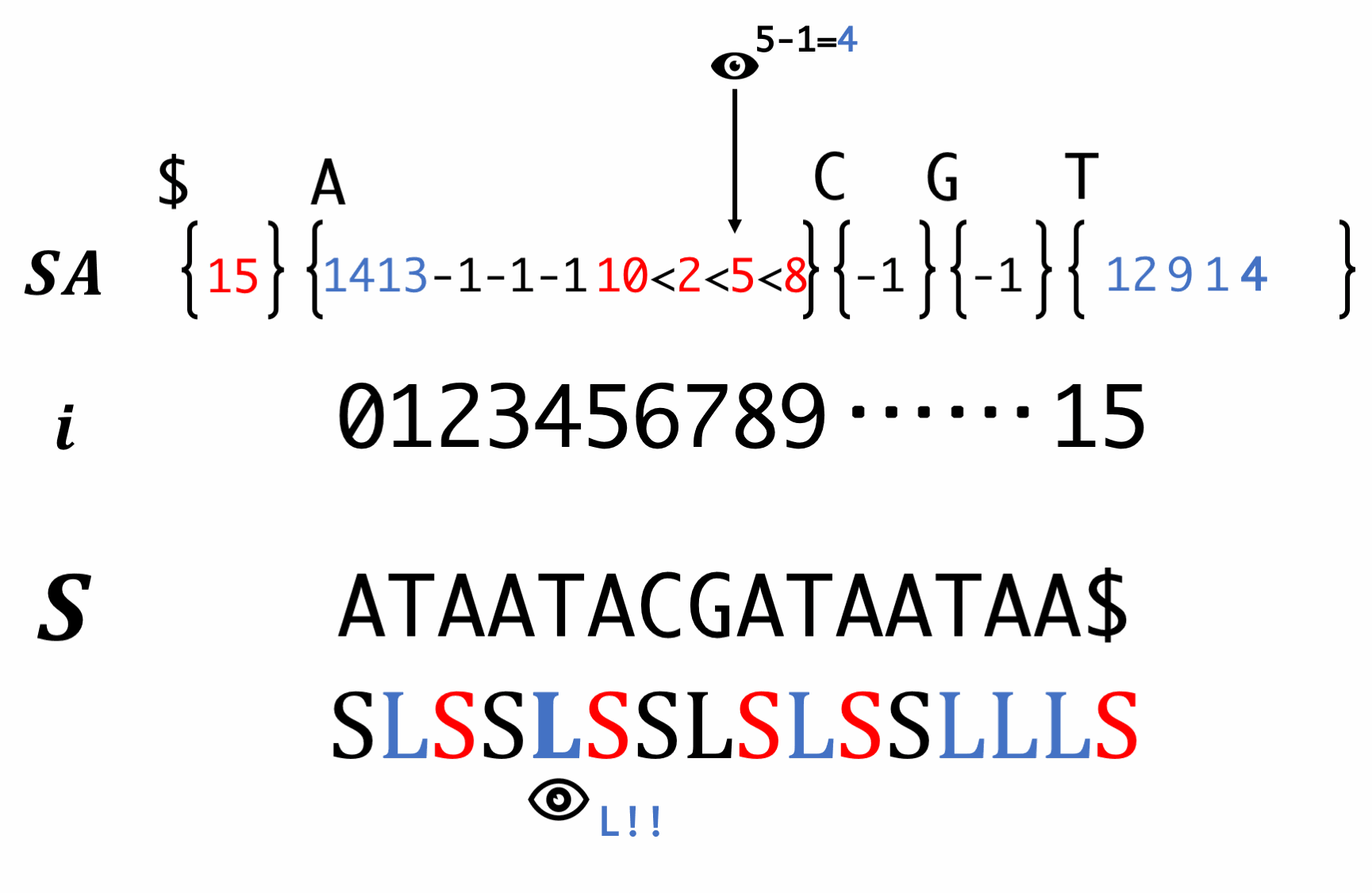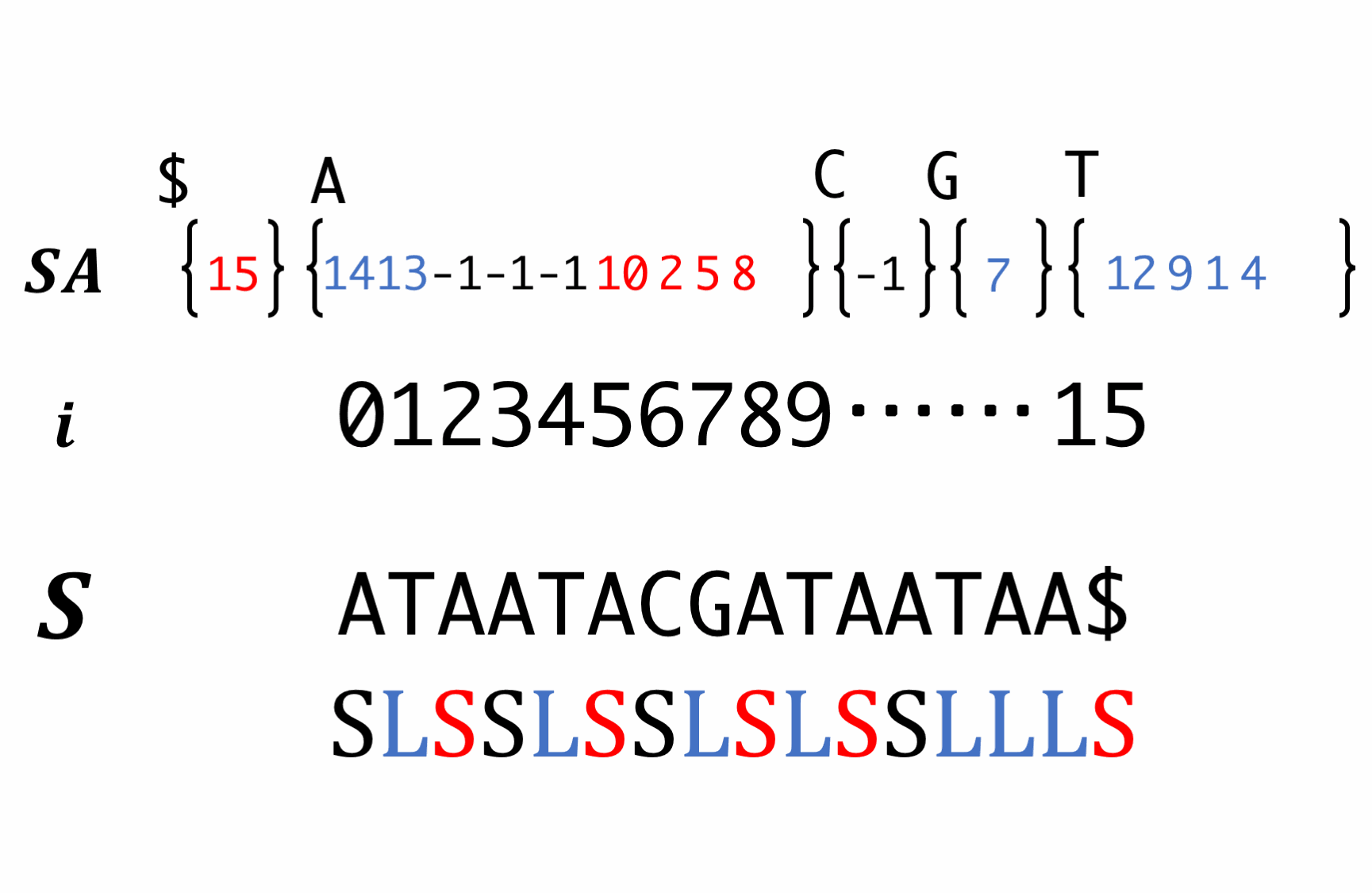
Step6. Induced sorting for L-type suffixes
Scan SA in forward order and fill L-type suffixes. If \(S[\text{Focusing Number}-1]\) is L-type, put \(\text{Focusing Number}-1\) into the corresponding bucket from the smaller. This is justified by
- Same bucket (Same initial)
- L-tyep (Smaller than S-type)
- One right is the smallest of the rest.
Step7. Induced sorting for S-type suffixes
Scan SA in backward order and fill S-type suffixes. At this time, we have to reorder the LMS.
 |
 |
 |
Finally, we get

How to Sort LMS suffix?? (Step5)
We could sort entire SA if LMS is correctly sorted. Then How to sort LMS?? The answer of this question is "Sort without Sorting".
Recursion of SA-IS
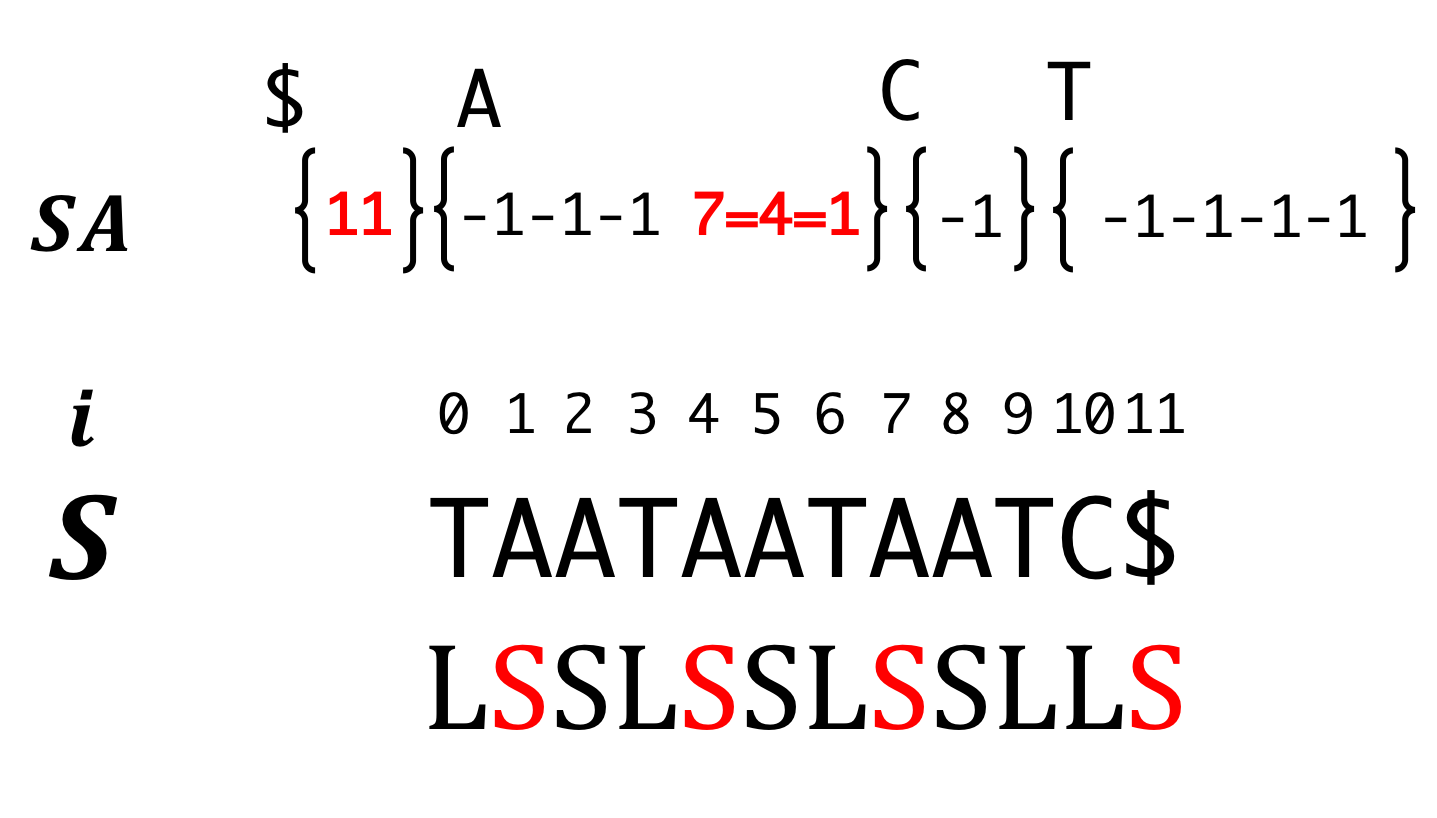
Step4'

Step5'
At this time, we couldn't know the order of LMS, so we "equality" instead of "inequality".
Step6'
Scan SA in forward order and fill L-type suffixes. At this moment, equality relationship is also passed.
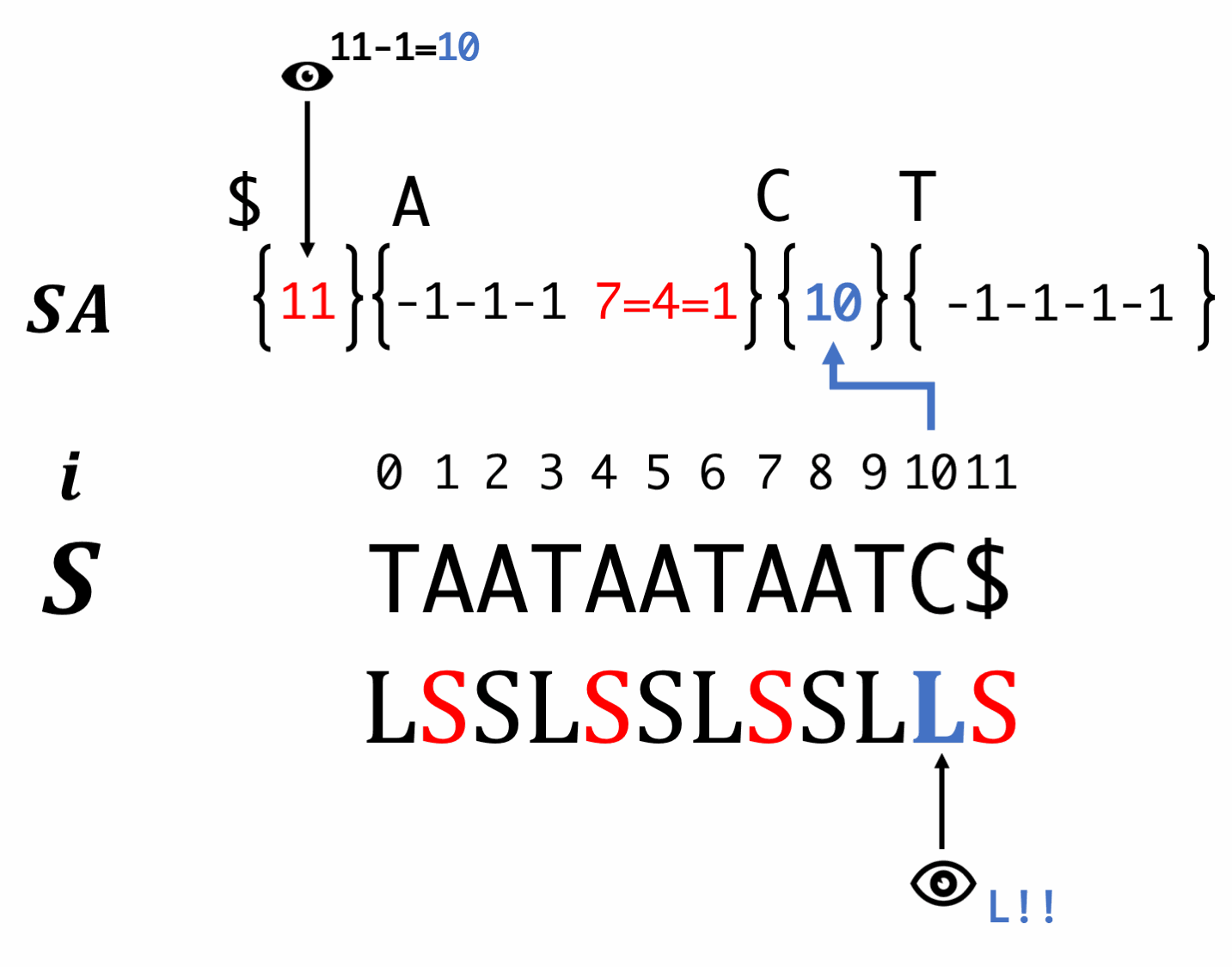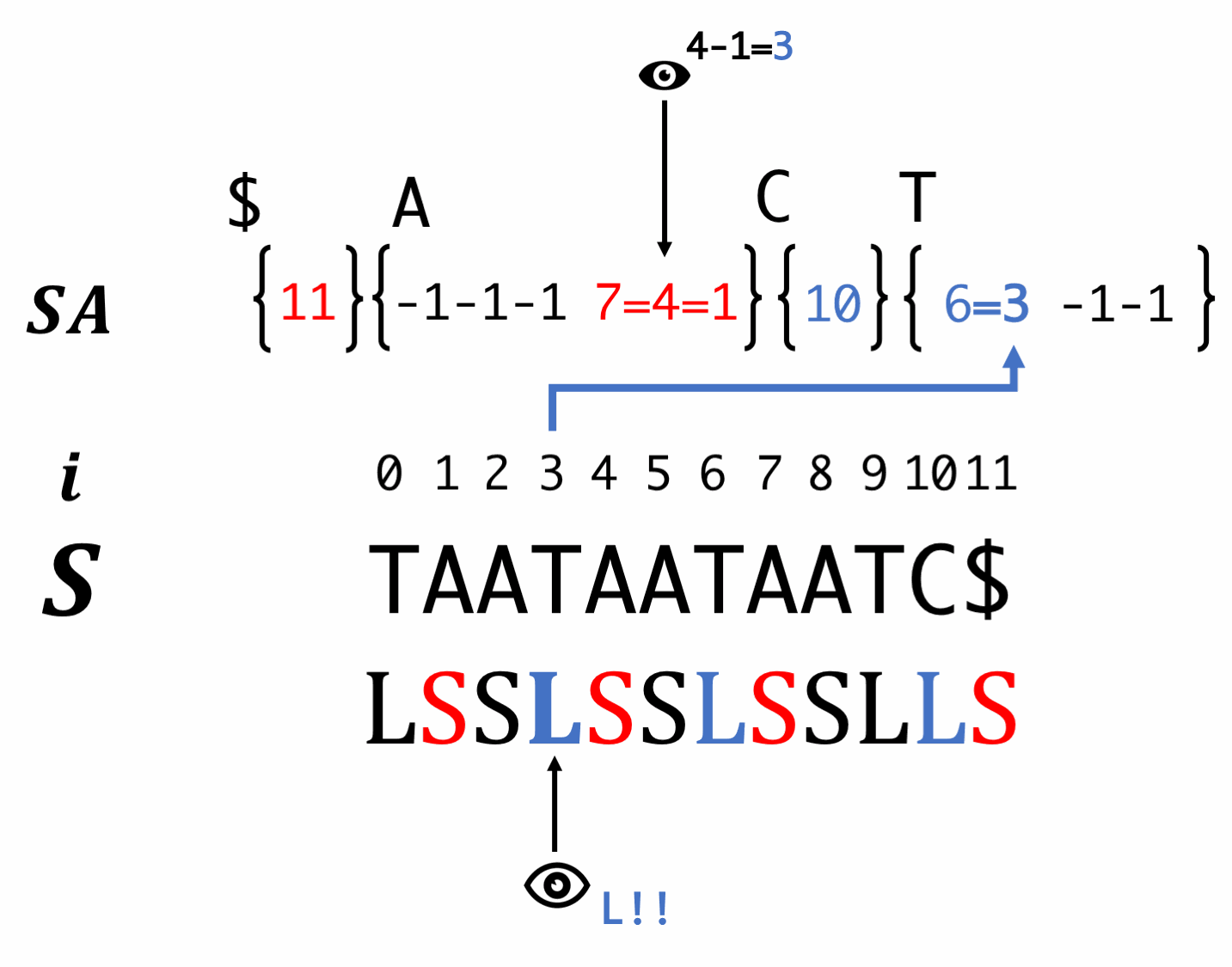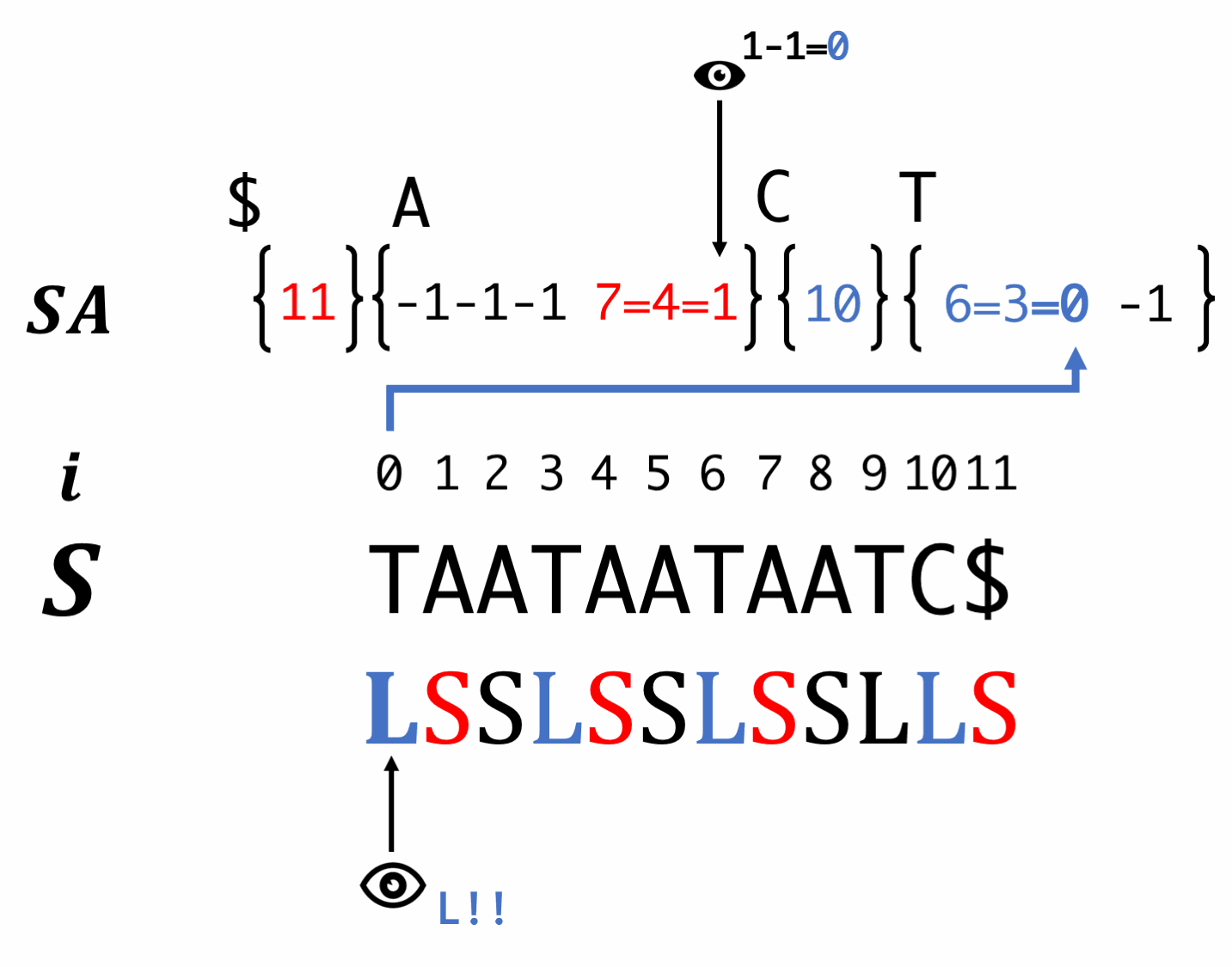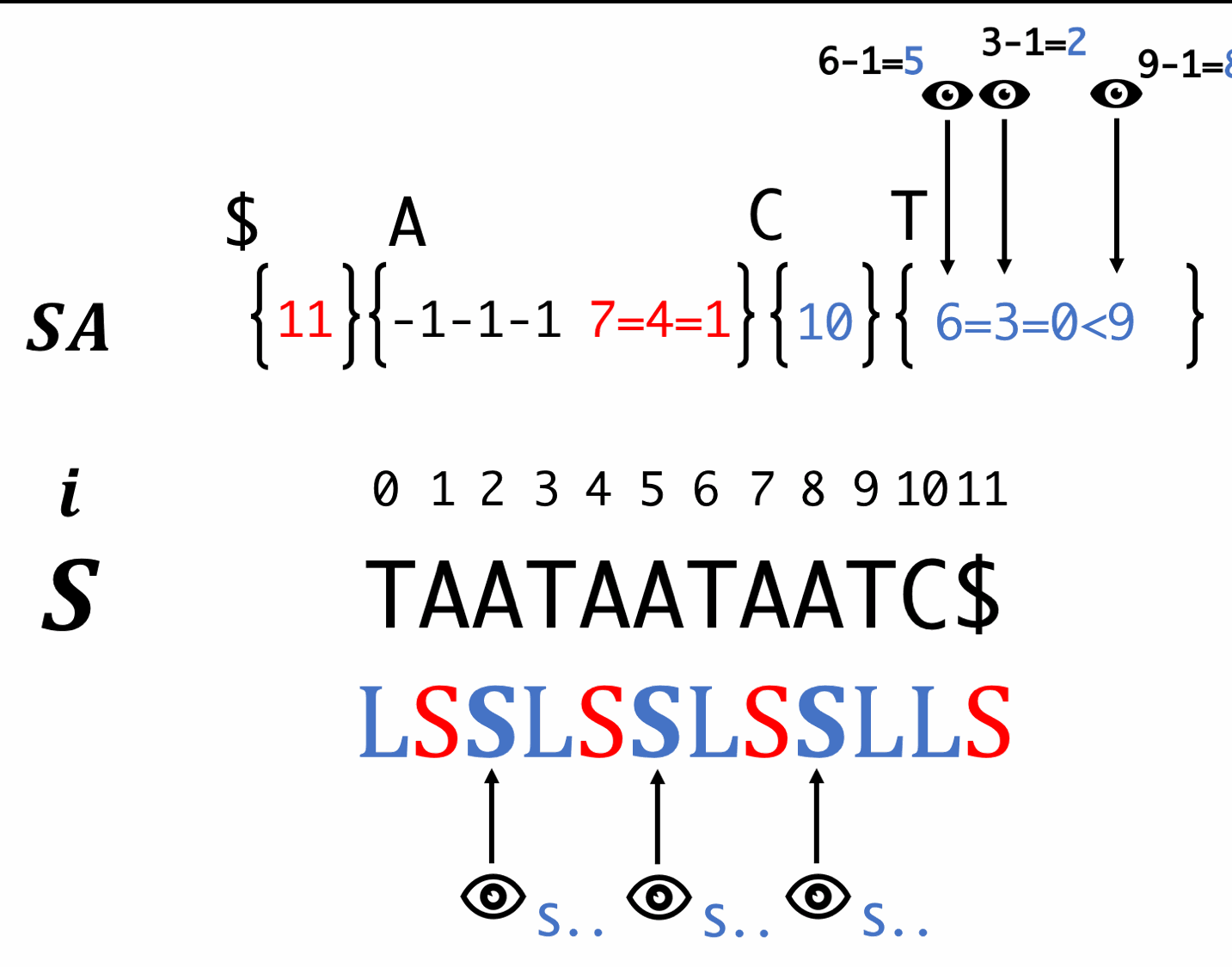
Step7'
Scan SA in backward order and fill S-type suffixes.
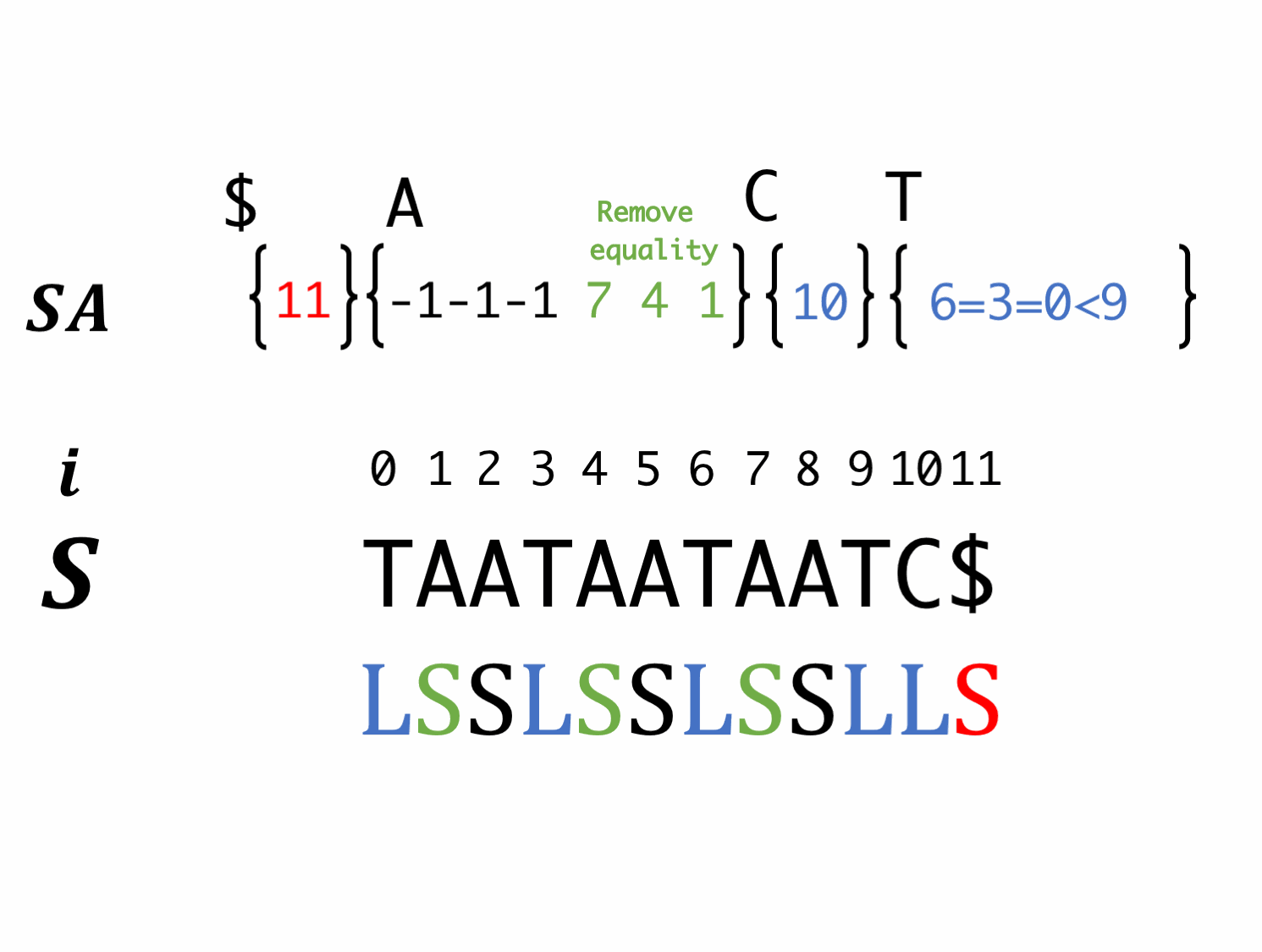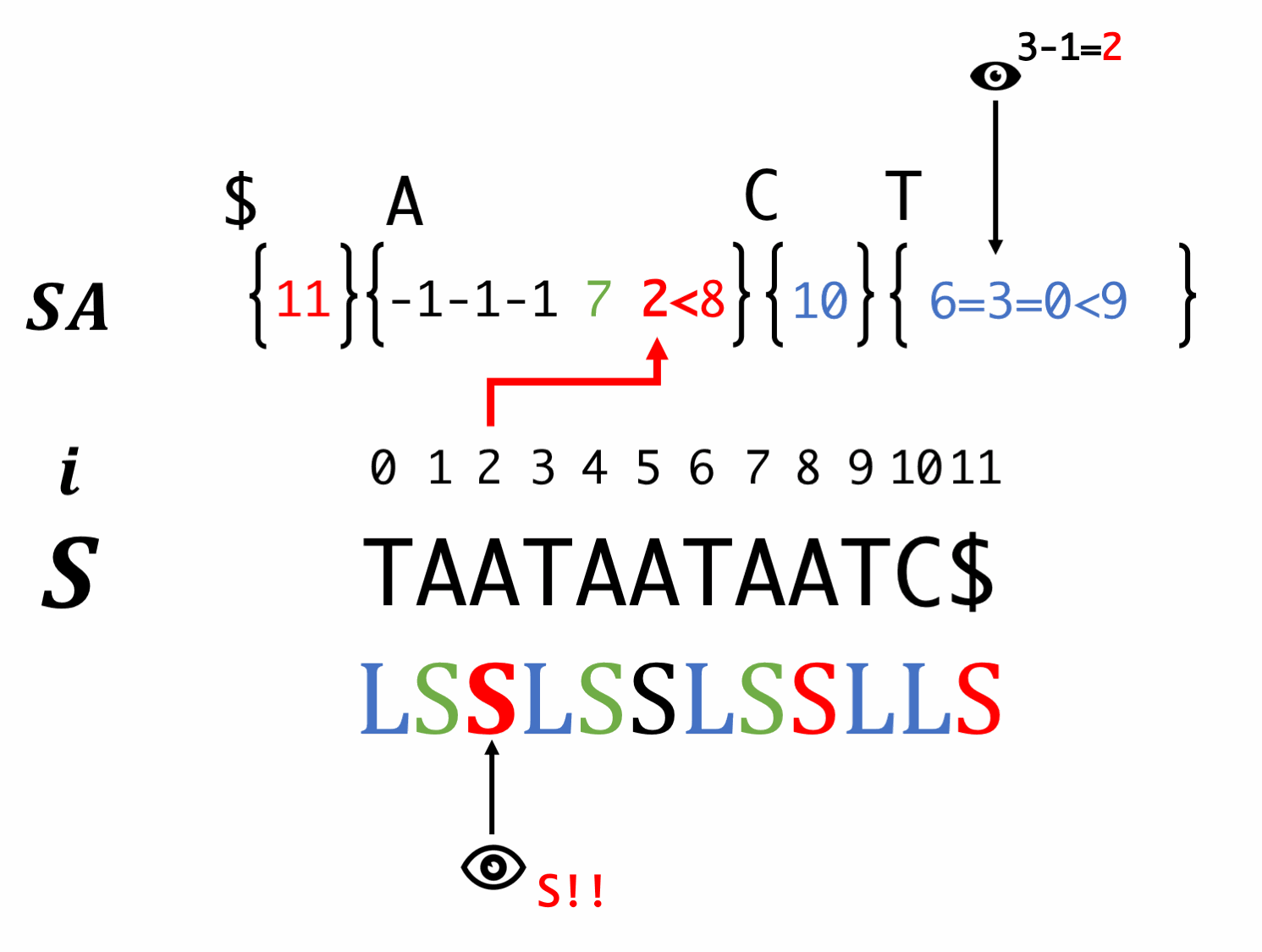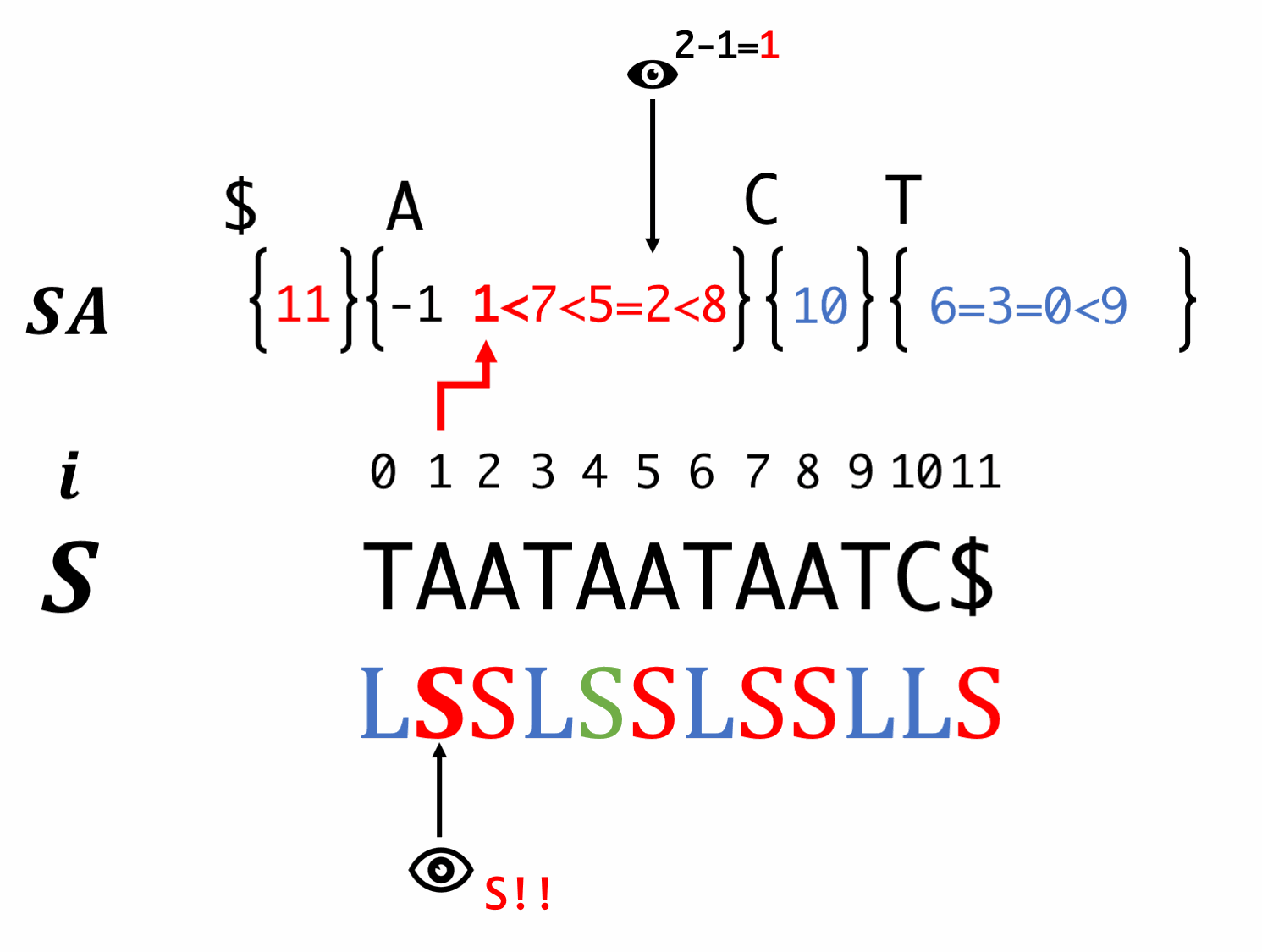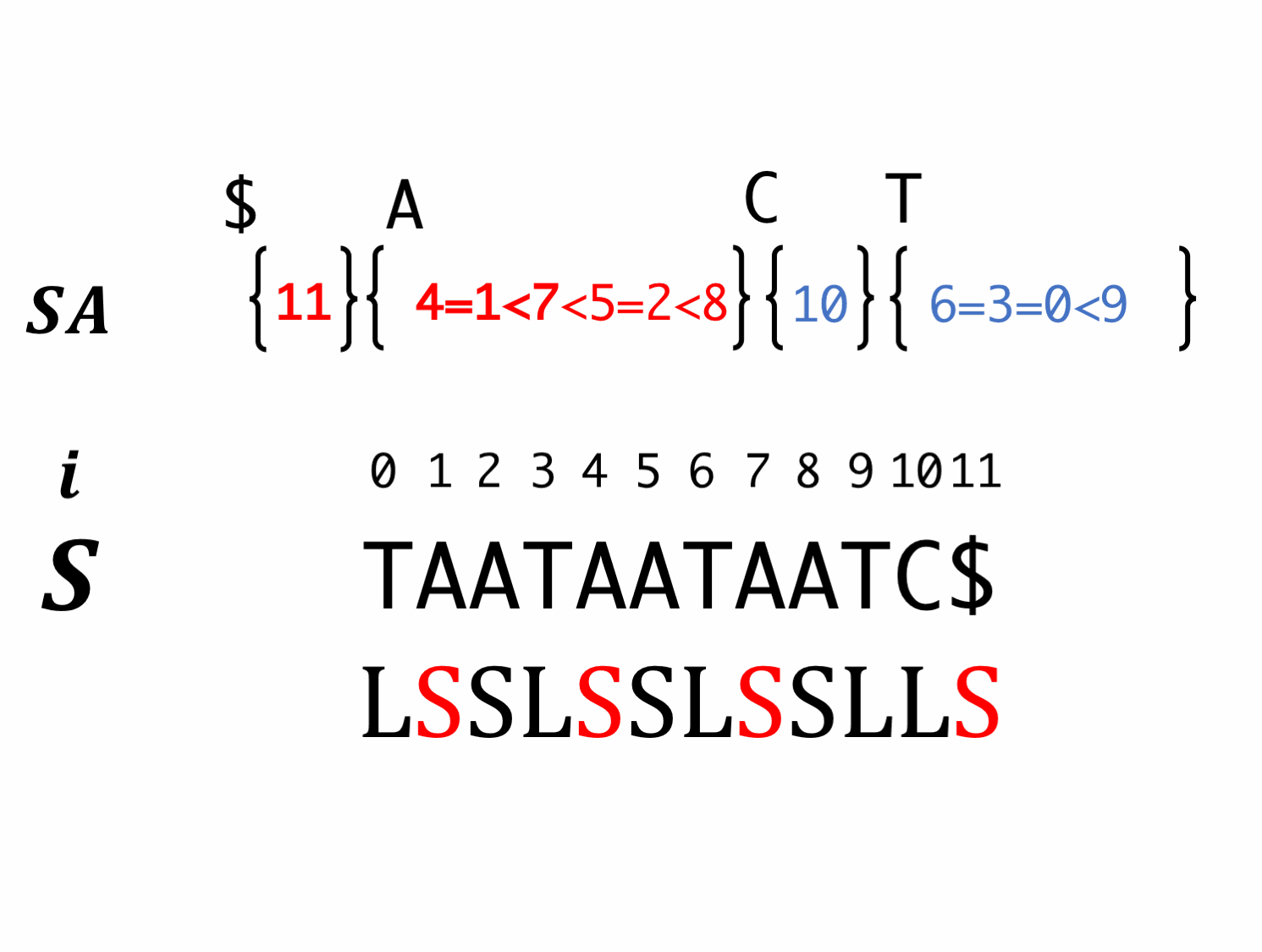
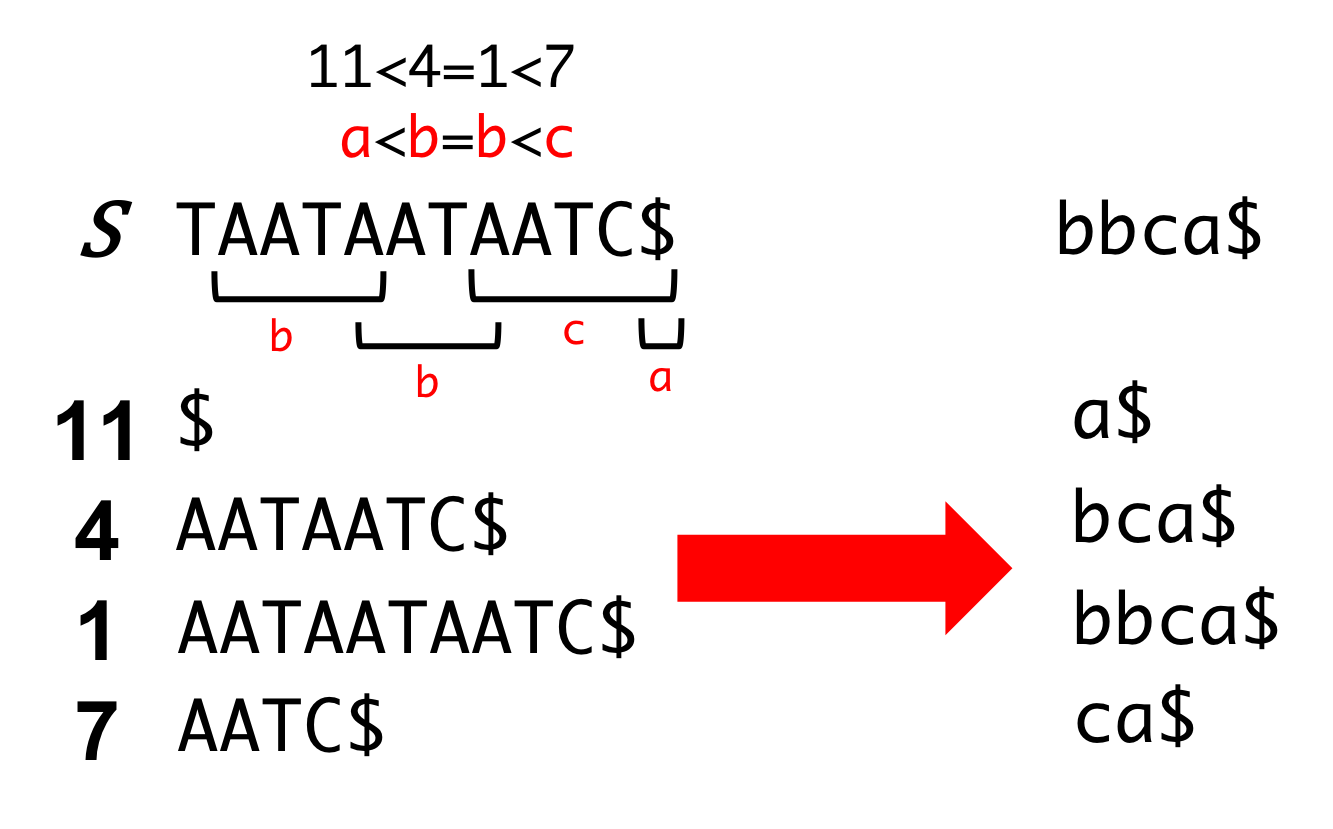
Encode LMS-substrings
Step5 (Recursion)
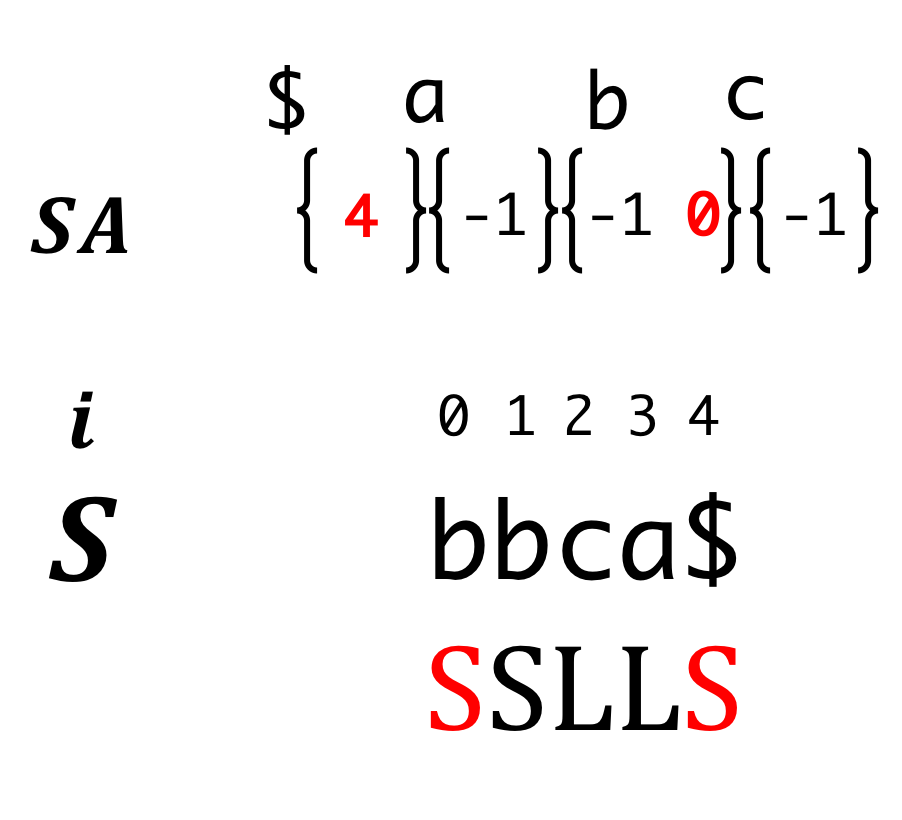
Step6 (Recursion)
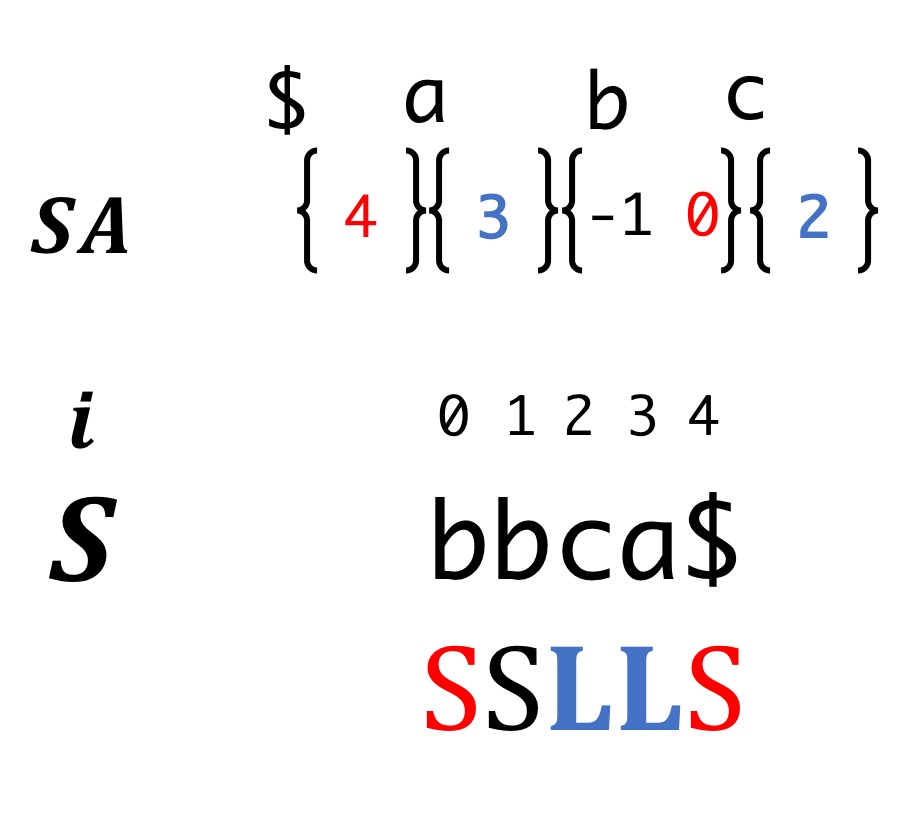
Step7 (Recursion)
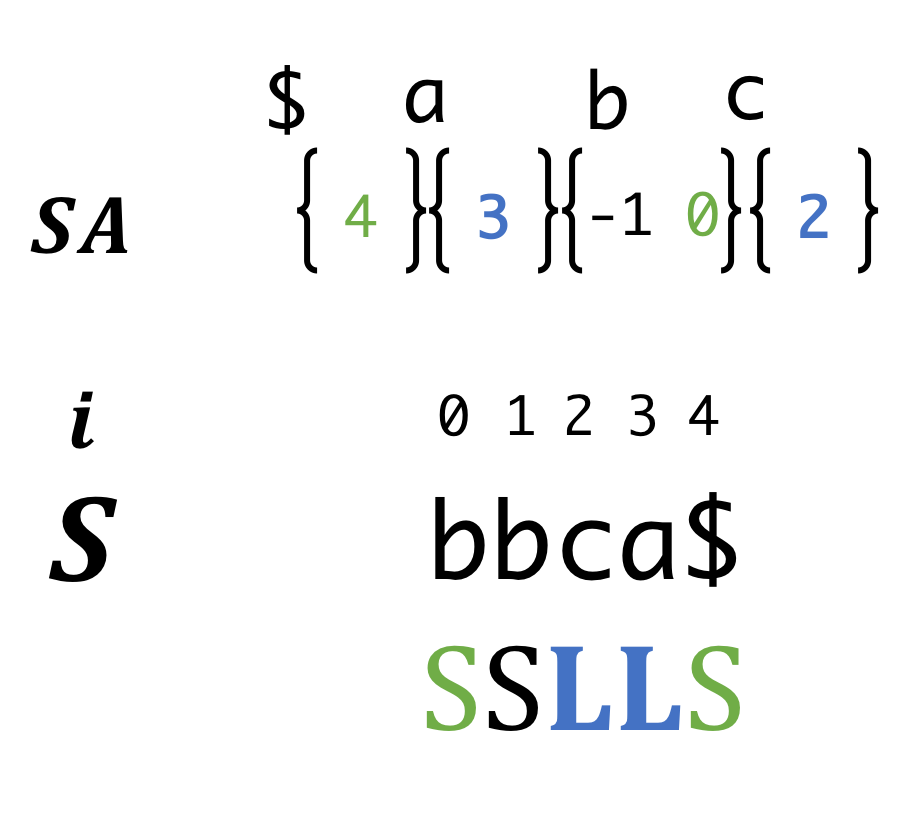 |
 |
We could sort LMS correctly!!
Computational complexity
In the each recursion step, it is guaranteed that the length of encoded strings is less than half of the previous length.
Burrows-Wheeler Transform; BWT
def kerasy.Bio.string.mkBWT(string, SA)
| Explanation | ex. S=TATAA$ |
|---|---|
| BWT(Burrows-Wheeler Transform) is the "characters just to the left of the suffixes in the suffix array", and it can be used to recover the entire string. It is given by $$BWT[i] = \begin{cases}S[SA[i] - 1] & (\text{if $SA[i]>0$})\\\mathrm{\$} & (\text{otherwise})\end{cases}$$
|
 |
BWT is useful for compression, since it tends to rearrange a character string into runs of similar characters. More importantly, this transformation is reversible, without needing to store any additional data. The BWT is thus a "free" method of improving the efficiency of text compression algorithms, costing only some extra computation.
Reverse BWT with Suffix Array
We will denote \(T\) and \(ISA\) as followings.
This means that the order of suffix whose initial character is \(BWT[i]\) is \(T[i]\), and under the above definition, the following equation holds.
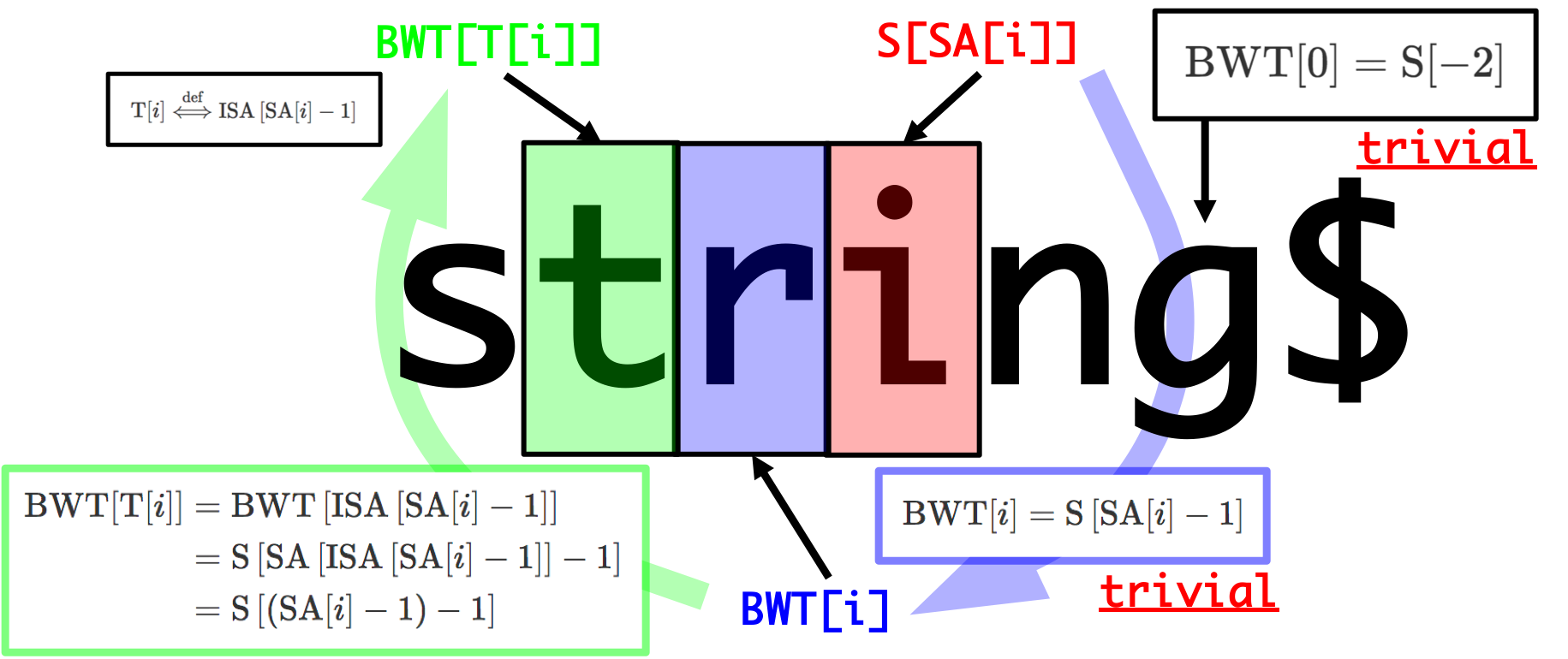
Now that we can get the original \(S\) from BWT and SA.
Reverse BWT without Suffix Array
In fact, we could recover the original strings only from BWT, because we can make \(T\) only from BWT. One of the important properties to realize it is LF Mapping.
LF Mapping
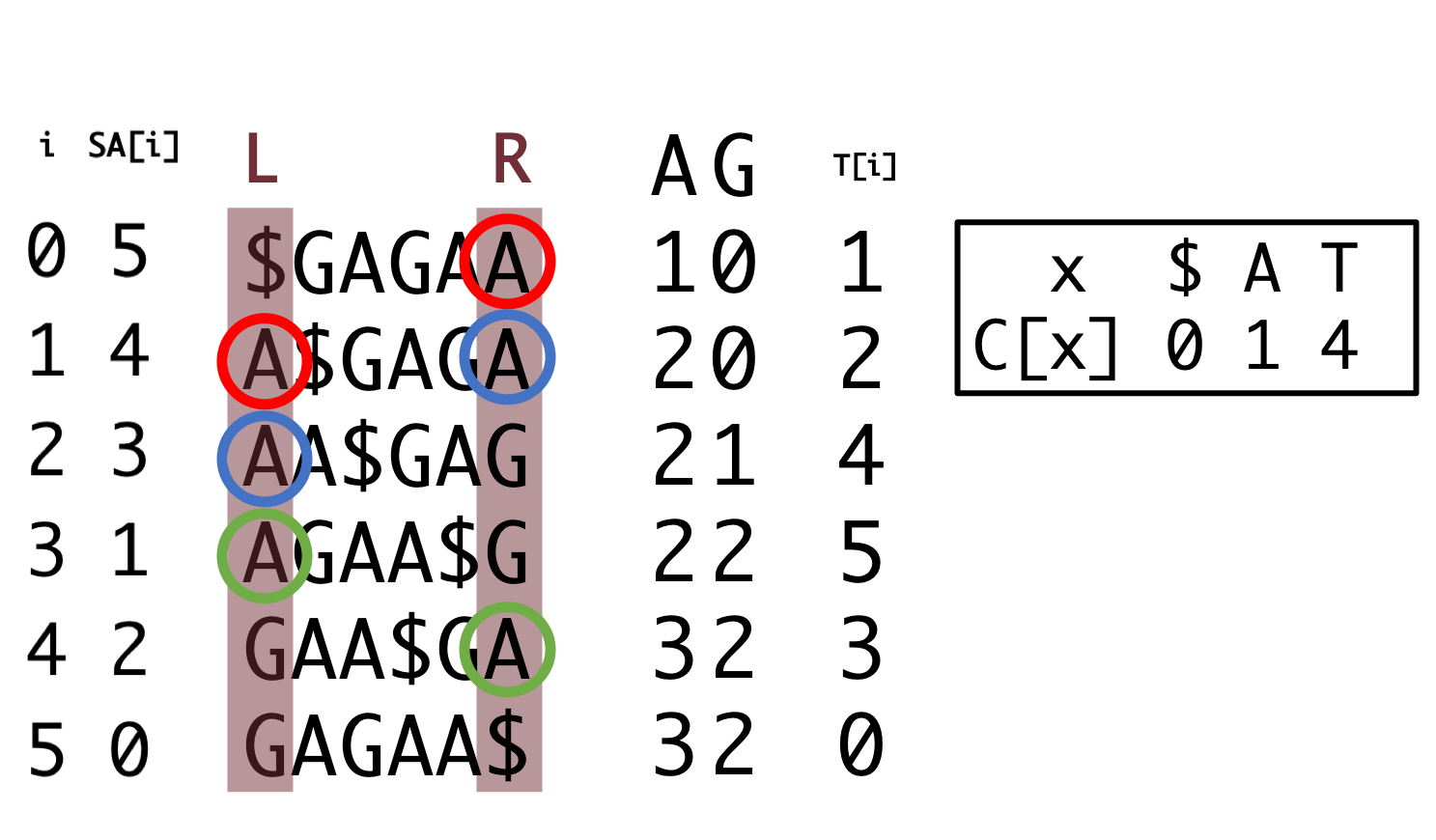
To calculate \(T[i]\) only from BWT, we will introduce auxiliary storages \(C[x]\), and \(Occ(x,i)\)
| Name | Explanation |
|---|---|
| \(C[x]\) | the total occurrence of a characters which is smaller than \(x\) in lexicographical order in BWT. |
| \(Occ(x,i)\) | the total occurrence of a character \(x\) up to \(i\)-th in the BWT. |
Using these variable, we can calculate \(T[i]\) by
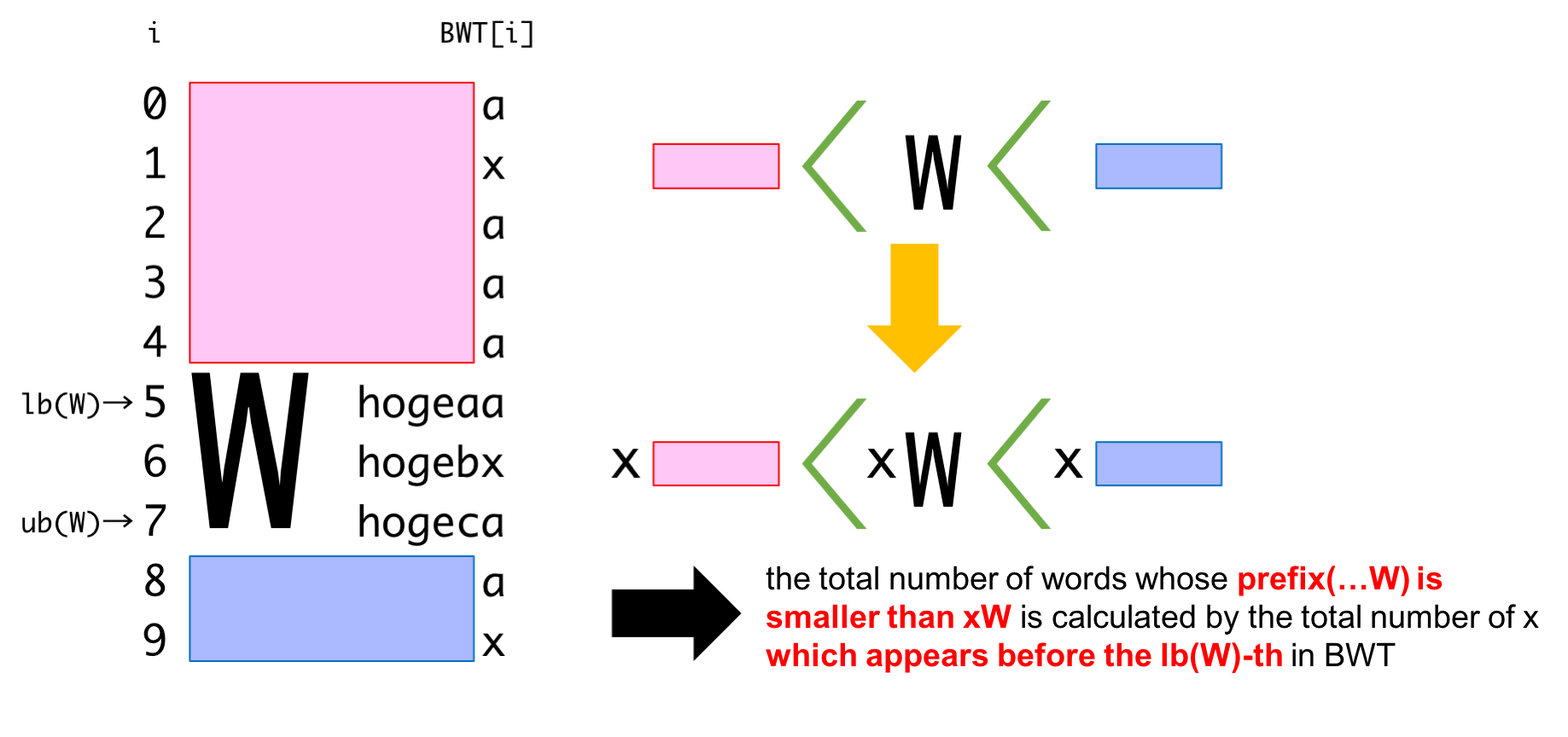
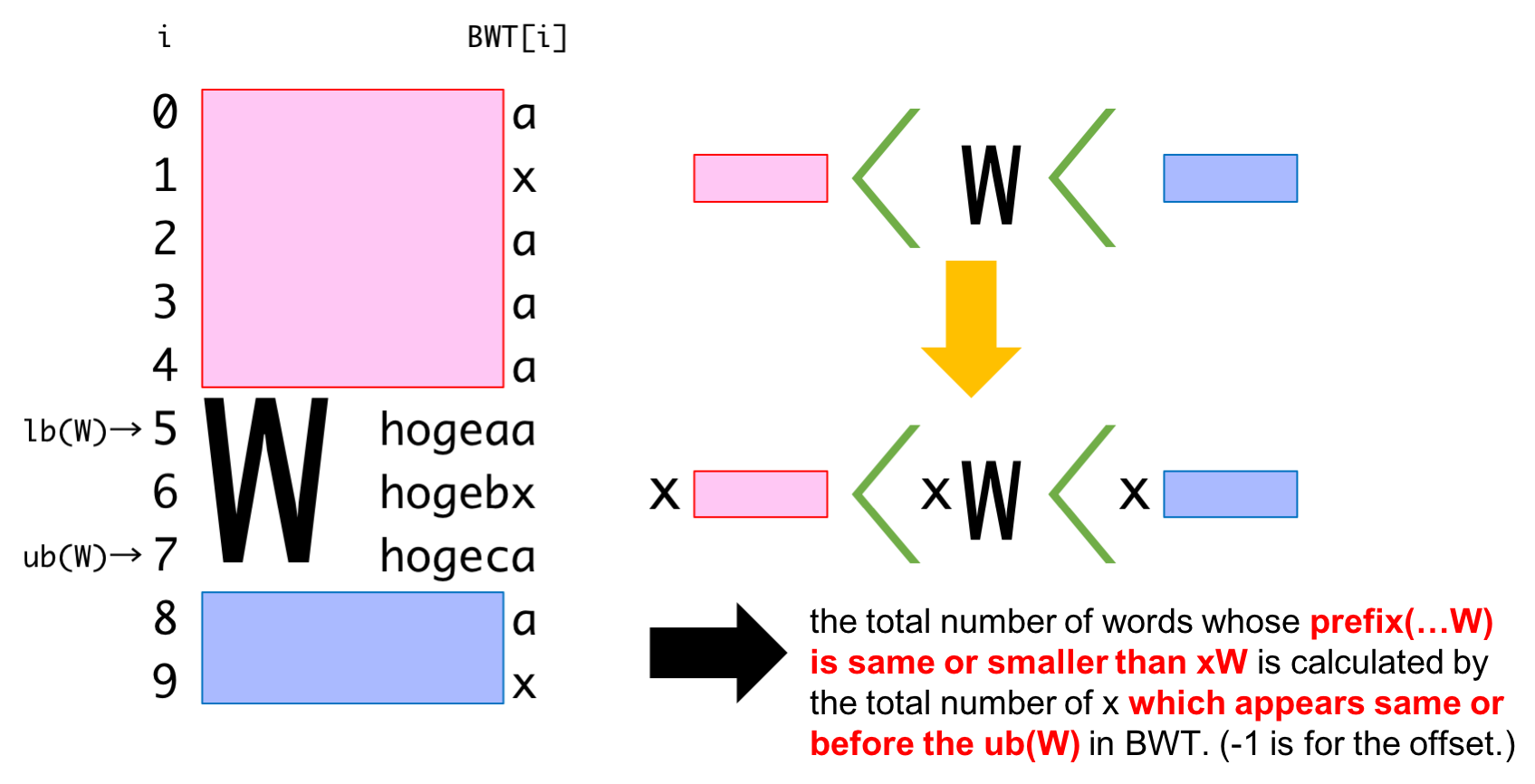
The above formula is guaranteed by the following properties.
These properties (especially the recursion (1) and (2)) are proved by
| \((1)\) | \((2)\) |
|---|---|
 |
 |
This allows us to search the occurrence range of characters with a specific prefix.
Longest Common Prefix; LCP
def kerasy.Bio.string.mkHeight(string, SA)
LCP(Longest Common Prefix) is "how many characters two strings have in common with each other", and LCP array is an array where each adjacent index stores lcp between \(i\)-th suffix and \(i+1\)-th suffix.
Speaking of LCParray, it usually refers to the suffix array,
Reference
- Linear-Time Longest-Common-Prefix Computation in Suffix Arrays and Its Applications
(If you read this paper, please look this. It will help to read.)