Secondary Structure

Notebook

Example Notebook: Kerasy.examples.structure.ipynb

Free energy minimization of RNA secondary structure

In cells, RNAs are likely to form energetically stable secondary structure, so the correctness of secondary structure should be evaluated based on the free energy.

Nussinov Algorithm

Nussinov Algorithm calculate the free energy by the number of base-pairs.

class kerasy.Bio.structure.Nussinov(**kwargs)
  • params:
    • nucleic_acid
    • WatsonCrick
    • minspan
variable definition
$$\gamma\left(i,j\right)$$
 the maximum number of base-pairs for subsequence from \(i\) to \(j\).
$$\omega\left(i,j\right)$$
 the maximum number of base-pairs excluding subsequence from \(i\) to \(j\).
$$Z(i,j)$$
 the maximum number of base-pairs if \(x_i\) and \(y_j\) form base pair.
$$ \begin{aligned} \gamma(i,j) &= \max \begin{cases} \gamma(i+1,j)\\ \gamma(i,j-1)\\ \gamma(i+1,j-1)+\delta(i,j)\\ \max_{i\leq k\verb|<|j}\left[\gamma(i,k) + \gamma(k+1,j)\right] \end{cases}\\ \omega(i,j) &= \max \begin{cases} \omega(i-1,j)\\ \omega(i,j+1)\\ \omega(i-1,j+1)+\delta(i-1,j+1)\\ \max_{1\leq k\verb|<|i}\left[\omega(k,j) + \gamma(k,i-1)\right]\\ \max_{j\verb|<| k\leq L}\left[\omega(j+1,k) + \gamma(i,k)\right] \end{cases}\\ Z(i,j) &= \begin{cases} \gamma\left(i+1,j-1\right) + 1 + \omega\left(i,j\right) & (\text{if }i\text{ and }j\text{-th nucleotides can form a base-pair})\\ 0 & (\text{otherwise}) \end{cases} \end{aligned} $$

Zuker Algorithm

class kerasy.Bio.structure.Zuker(**kwargs)
  • params:
    • nucleic_acid
    • WatsonCrick
    • hairpin
    • internal
    • buldge
    • a
    • b
    • c
    • stacking_cols
    • stacking_score

The free energy of a secondary structure is approximated as the sum of the free energy of "loops".

$$E = \sum_iE_i$$

The free energy of individual loop is given by experimental data. (ex. \(\mathrm{C-G: }-3.4\mathrm{kcal/mol}\), \(\mathrm{U-A: }-0.9\mathrm{kcal/mol}\))

Five types of "loops"

hairpin loop stacking bulge loop internal loop multi-loop
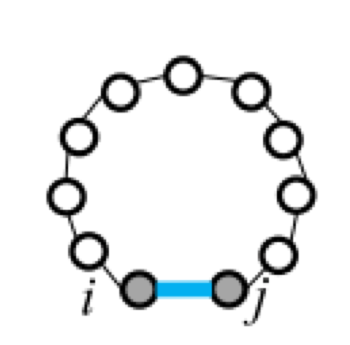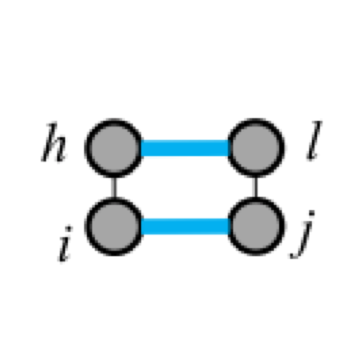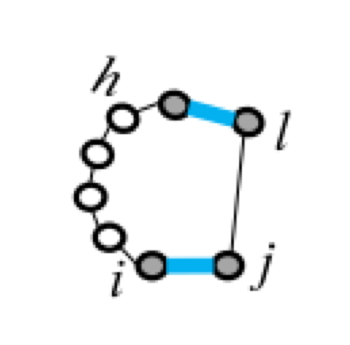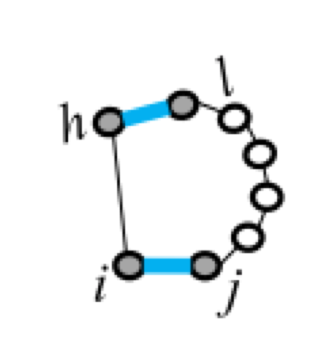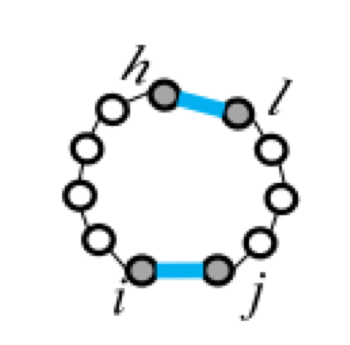F1(i,j) F2(i,j,h,l) Fm=a+bk+cu
  • a,b,c: constant
  • k: the number of base-pairs in a multi-loop
  • u: the number of single stranded nucleotides in a multi-loop
variable meaning
\(W(i,j)\) the minimum free energy of subsequence from \(i\) to \(j\).
\(V(i,j)\) the minimum free energy of subsequence from \(i\) to \(j\) when \(i\) to \(j\) forms a base-pair.
\(M(i,j)\) the minimum free energy of subsequence when subsequence from \(i\) to \(j\) are in the multi-loop and contain one or more base pairs which close it.
$$ \begin{aligned} W(i,j) &= \min \begin{cases} W(i+1,j)\\W(i,j-1)\\V(i,j)\\\min_{i\leq k<j}\left\{W(i,k) + W(k+1,j)\right\} \end{cases}\\ V(i,j) &= \min \begin{cases} F_1(i,j)\\\min_{i<h<l<j}F_2(i,j,h,l) + V(h,l)\\\min_{i+1\leq k<j-1}\left[M(i+1,k) + M(k+1,j)\right]+a+b \end{cases}\\ M(i,j) &= \min \begin{cases} V(i,j)+b\\M(i+1,j)+c\\M(i,j-1)+c\\\min_{i\leq<k<j}\left[M(i,k) + M(k+1,j)\right] \end{cases}\\ \end{aligned} $$

Warning

None of the algorithms we see this week can deal with pseudoknot

Pseudoknot